Báo cáo học liệu
Mua học liệu
Mua học liệu:
-
Số dư ví của bạn: 0 coin - 0 Xu
-
Nếu mua học liệu này bạn sẽ bị trừ: 2 coin\Xu
Để nhận Coin\Xu, bạn có thể:

Tóm tắt kiến thức: Hàm số lượng giác SVIP

1. Hàm số chẵn - lẻ
Định nghĩa
Cho hàm số $y=f(x)$ với tập xác định $D$.
+ Hàm số $y=f(x)$ được gọi là hàm số chẵn nếu $\forall x\in D$ thì $-x\in D$ và $f(-x)=f(x)$.
+ Hàm số $y=f(x)$ được gọi là hàm số lẻ nếu $\forall x\in D$ thì $-x\in D$ và $f(-x)=-f(x)$.
Chú ý
+ Đồ thị hàm số chẵn nhận trục tung làm trục đối xứng.
+ Đồ thị hàm số lẻ nhận gốc toạ độ làm tâm đối xứng.
2. Hàm số tuần hoàn
Cho hàm số $y=f(x)$ với tập xác định $D$. Hàm số $y=f(x)$ được gọi là tuần hoàn nếu tồn tại một số $T$ khác 0 sao cho với mọi $x\in D$, ta có:
⚡$x+T\in D$ và $x-T\in D$
⚡$f(x+T)=f(x)$.
Số $T$ dương, nhỏ nhất thoả mãn (nếu có) các tính chất trên được gọi là chu kì của hàm số đó.
3. Hàm số sin, hàm số côsin
| Hàm số sin | Hàm số côsin | |
| TXĐ | $\mathbb{R}$ | $\mathbb{R}$ |
| Đồ thị | 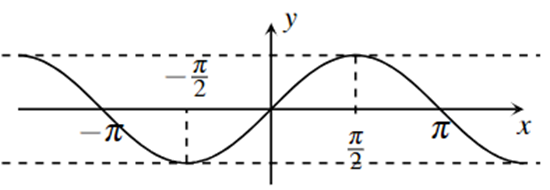 |
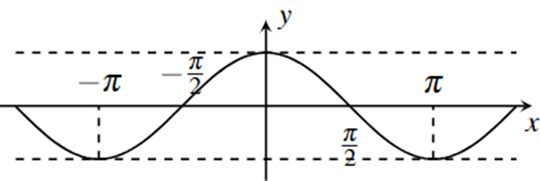 |
| Tính chẵn, lẻ | hàm số lẻ, có đồ thị đối xứng qua gốc tọa độ O | hàm số chẵn, có đồ thị đối xứng qua trục tung |
| Chu kì tuần hoàn | $2\pi $ | $2\pi $ |
| Đơn điệu |
đồng biến trên mỗi khoảng $\Big( -\dfrac{\pi }{2}+k2\pi ;\dfrac{\pi }{2}+k2\pi \Big)$; nghịch biến trên mỗi khoảng $\Big( \dfrac{\pi }{2}+k2\pi ;\dfrac{3\pi }{2}+k2\pi \Big)$ với $k\in \mathbb{Z}$. |
đồng biến trên mỗi khoảng $(-\pi +k2\pi ;k2\pi )$; nghịch biến trên mỗi khoảng $(k2\pi ;\pi +k2\pi )$ với $k\in \mathbb{Z}$. |
4. Hàm số tang, hàm số côtang
| Hàm số tang | Hàm số côtang | |
| TXĐ | $D=\mathbb{R}\backslash \Big\{ \dfrac{\pi }{2}+k\pi \,|\,k\in \mathbb{Z} \Big\}$ | $D=\mathbb{R}\backslash \left\{ k\pi \,|\,k\in \mathbb{Z} \right\}$ |
| Đồ thị | 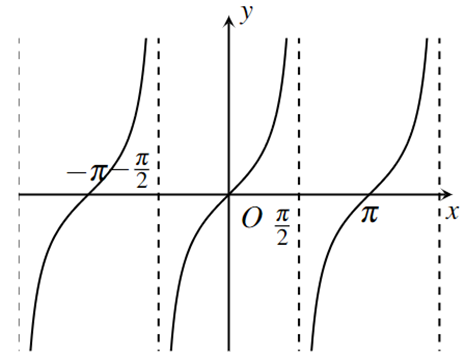 |
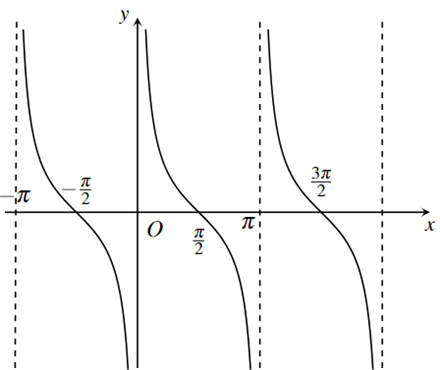 |
| Tính chẵn, lẻ | hàm số lẻ, có đồ thị đối xứng qua gốc tọa độ O | hàm số lẻ, có đồ thị đối xứng qua gốc tọa độ O |
| Chu kì tuần hoàn | $\pi $ | $\pi $ |
| Đơn điệu |
đồng biến trên mỗi khoảng $\Big( -\dfrac{\pi }{2}+k\pi ;\dfrac{\pi }{2}+k\pi \Big)$, với $k\in \mathbb{Z}$. |
nghịch biến trên mỗi khoảng $\left( k\pi ;\pi +k\pi \right)$, với $k\in \mathbb{Z}.$ |

Dạng 1. Tập xác định của hàm số
$y=\dfrac{f\left( x \right)}{g\left( x \right)}$ xác định khi $g\left( x \right)\ne 0$.
$y=\sqrt{f\left( x \right)}$ xác định khi $f\left( x \right)\ge 0$.
$y=\tan \left[ u\left( x \right) \right]$ xác định khi $u\left( x \right)$ xác định và $u\left( x \right)\ne \dfrac{\pi }{2}+k\pi ,\,k\in \mathbb{Z}$.
$y=\cot \left[ u\left( x \right) \right]$ xác định khi $u\left( x \right)$ xác định và $u\left( x \right)\ne k\pi , \,k\in \mathbb{Z}$.
Ví dụ 1. Tìm tập xác định của hàm số $y=\tan \Big( 2x-\dfrac{\pi }{3} \Big)$.
Lời giải
$\cos \left( 2x-\dfrac{\pi }{3} \right)\ne 0\Leftrightarrow 2x-\dfrac{\pi }{3}\ne \dfrac{\pi }{2}+k\pi \Leftrightarrow x\ne \dfrac{5\pi }{12}+\dfrac{k\pi }{2}$, $k\in \mathbb{Z}$.
Vậy tập xác định của hàm số đã cho là $D = \mathbb{R} \backslash \Big\{\dfrac{5\pi }{12}+\dfrac{k\pi }{2} \, \big| \, k\in \mathbb{Z}\Big\}$.
Dạng 2. Xét tính chẵn lẻ của hàm số lượng giác
⚡Tìm TXĐ $D$ của hàm số và kiểm tra $D$ là tập đối xứng?
▪️ Nếu $x\in D$ và $-x\in D$ thì $D$ đối xứng;
▪️ Nếu $D$ không đối xứng thì hàm số không chẵn, không lẻ.
⚡Tính $f\left( -x \right)$, chỗ nào có $x,$ ta thay bằng $-x$.
▪️ Nếu $f\left( -x \right)=f\left( x \right)$ thì hàm số chẵn;
▪️ Nếu $f\left( -x \right)=-f\left( x \right)$ thì hàm số lẻ;
▪️ Còn lại, hàm số không chẵn, không lẻ.
Ví dụ 2. Hàm số $y=\dfrac{\cos x}{x^3}$ là hàm số lẻ hay không?
Lời giải
Tập xác định $D=\mathbb{R}\backslash\{0\}$ là tập đối xứng.
$f\left( -x \right)=\dfrac{\cos (-x)}{-x^3}=-\dfrac{\cos x}{x^3}=-f\left( x \right).$
Do đó hàm số $y=\dfrac{\cos x}{x^3}$ là hàm số lẻ.
Dạng 3. Tính tuần hoàn của hàm số
⚡Chứng minh hàm số $y=f\left( x \right)$ tuần hoàn:
Xét hàm số $y=f\left( x \right)$, tập xác định $D$, ta dự đoán số thực dương $T_0$ sao cho $\left\{ \begin{aligned} & \forall x\in D: \,x-{{T}_{0}}\in D;\,x+{{T}_{0}}\in D \\ & f\left( x+{{T}_{0}} \right)=f\left( x \right) \\ \end{aligned} \right.$
⚡Dự đoán chu kì tuần hoàn:
▪️ Hàm số $y=\sin x;\, y=\cos x$ tuần hoàn với chu kì $2\pi $.
▪️ Hàm số $y=\tan x;\, y=\cot x$ tuần hoàn với chu kì $\pi $.
▪️ Hàm số $y=\sin \left( ax+b \right);\, y=\cos \left( ax+b \right), \,\left( a\ne 0 \right)$ tuần hoàn với chu kì $\dfrac{2\pi }{\left| a \right|}$.
▪️ Hàm số $y=\tan \left( ax+b \right);\, y=\cot \left( ax+b \right), \,\left( a\ne 0 \right)$ tuần hoàn với chu kì $\dfrac{\pi }{\left| a \right|}$.
▪️ Hàm số $y=F\left( x \right)=m.f\left( x \right)+n.g\left( x \right)$ tuần hoàn với chu kì $T$ là “bội chung nhỏ nhất” của $a$ và $b$.
Ví dụ 3. Chu kì của hàm số $y=\cos 2x$ là bao nhiêu?
Lời giải
Chu kì của hàm số $y=\cos 2x$ là: $T=\dfrac{2\pi }{2}=\pi $.
Dạng 4. Giá trị lớn nhất, giá trị nhỏ nhất của hàm số lượng giác
Cách 1: Bất đẳng thức cơ bản
▪️ $-1\le \sin x\le 1, \,\forall x\in \mathbb{R}$;
▪️ $-1\le \cos x\le 1,\, \forall x\in \mathbb{R}$;
▪️ $0\le {{\sin }^{2}}x,\, {{\cos }^{2}}x\le 1,\, \forall x\in \mathbb{R}$;
▪️ $0\le \left| \sin x \right|,\, \left| \cos x \right|\le 1, \,\forall x\in \mathbb{R}$;
Cách 2: Điều kiện có nghiệm
▪️ $\sin x=f\left( m \right)$ có nghiệm khi $-1\le f\left( m \right)\le 1$.
▪️ $\cos x=f\left( m \right)$ có nghiệm khi $-1\le f\left( m \right)\le 1$.
▪️ $a\sin x+b\cos x=c$ có nghiệm khi ${{a}^{2}}+{{b}^{2}}\ge {{c}^{2}}$.
Cách 3: Lập bảng biến thiên để đưa ra kết luận
Ví dụ 4. Giá trị lớn nhất và giá trị nhỏ nhất của hàm số $y=3\sin \Big( x+\dfrac{3\pi }{4} \Big)-1$ lần lượt là bao nhiêu?
Lời giải
$-1\le \sin \Big( x+\dfrac{3\pi }{4} \Big) \le 1 \Leftrightarrow -3\le 3\sin \Big( x+\dfrac{3\pi }{4} \Big) \le 3$
$\Leftrightarrow -4\le 3\sin \Big( x+\dfrac{3\pi }{4} \Big)-1\le 2 \Rightarrow -4\le y\le 2$.
Vậy giá trị lớn nhất của hàm số $y=3\sin \Big( x+\dfrac{3\pi }{4} \Big)-1$ là $2$ khi $x=-\dfrac{\pi }{4}$.
Giá trị nhỏ nhất của hàm số $y=3\sin \Big( x+\dfrac{3\pi }{4} \Big)-1$ là $-4$ khi $x=\dfrac{3\pi }{4}$.
Dạng 5. Tính đơn điệu và đồ thị hàm số
Bạn có thể đăng câu hỏi về bài học này ở đây
