Tóm tắt kiến thức: Góc lượng giác SVIP

1. ĐƠN VỊ ĐO GÓC – ĐỘ DÀI CUNG TRÒN

Độ dài đường tròn là $2\pi R$ với $R$ là bán kính. Khi đó:

⚡$2\pi$ rad ứng với $360^\circ$.

⚡Cung tròn có số đo $a$ sẽ có độ dài là $l = R.a$.

2. GÓC LƯỢNG GIÁC

⚡Cho hai tia $Ou$, $Ov$. Nếu tia $Om$ quay chỉ theo chiều dương (hay chỉ theo chiều âm) xuất phát từ tia $Ou$ đến trùng với tia $Ov$ thì ta nói: Tia $Om$ quét một góc lượng giác với tia đầu $Ou$ và tia cuối $Ov$, kí hiệu là $(Ou,Ov)$

⚡Cho hai góc lượng giác $(Ou, Ov)$, $(Ou' , Ov')$ có tia đầu trùng nhau ($Ou \equiv Ou'$), tia cuối trùng nhau ($Ov \equiv Ov'$). Khi đó, nếu sử dụng đơn vị đo là độ thì ta có:

$(Ou , Ov) = (Ou' , Ov') + k.360^\circ$ với $k$ là số nguyên.

Nếu sử dụng đơn vị đo là radian thì công thức trên có thể viết như sau:

$(Ou , Ov) = (Ou' , Ov') + k.2\pi$ với $k$ là số nguyên.

3. HỆ THỨC CHASLES (SA – LƠ)

Với ba tia tuỳ ý $Ou, \, Ov, \, Ow$, ta có: $(Ou , Ov) + (Ov , Ow) = (Ou , Ow) + k2\pi$ (với $k \in \mathbb{Z}$) .

4. ĐƯỜNG TRÒN LƯỢNG GIÁC

⚡Trong mặt phẳng toạ độ đã được định hướng $Oxy$, lấy điểm $A(1;0)$. Đường tròn tâm $O$, bán kính $OA=1$ được gọi là đường tròn lượng giác (hay đường tròn đơn vị) gốc $A$.

⚡Tồn tại duy nhất điểm $M$ sao cho $(OA , OM) = a$. Điểm $M$ được gọi là điểm biểu diễn của góc có số đo $a$ trên đường tròn lượng giác.

Dạng 1. Mối liên hệ giữa đơn vị rađian và độ

🔹Đổi từ đơn vị độ sang đơn vị rad: $a^\circ = \dfrac a{180}\pi$

🔹Đổi từ đơn vị rad sang đơn vị độ: $\pi = 180^\circ$ nên $k\pi = k.180^\circ$

Ví dụ 1. Góc có số đo $108^\circ$ đổi sang đơn vị rađian ta được:

$\dfrac{108}{180}\pi = \dfrac{3\pi}5$.

Ví dụ 2. Góc có số đo $\dfrac{2\pi}5$ đổi sang đơn vị độ ta được:

$\dfrac{2\pi}5 = \dfrac{2.180^\circ}5 = 72^\circ$.

Dạng 2. Điểm biểu diễn của góc lượng giác trên đường tròn lượng giác

Xét cung lượng giác $AM$ ứng với góc lượng giác $\alpha = (OA , OM) = \beta + \dfrac{k2\pi}n$ thì $M$ gọi là điểm biểu diễn cho góc (cung) đó.

🔹Số điểm biểu diễn $M_1; \, M_2; \, ... ; \, M_n$ của $\alpha$ là $n$ điểm.

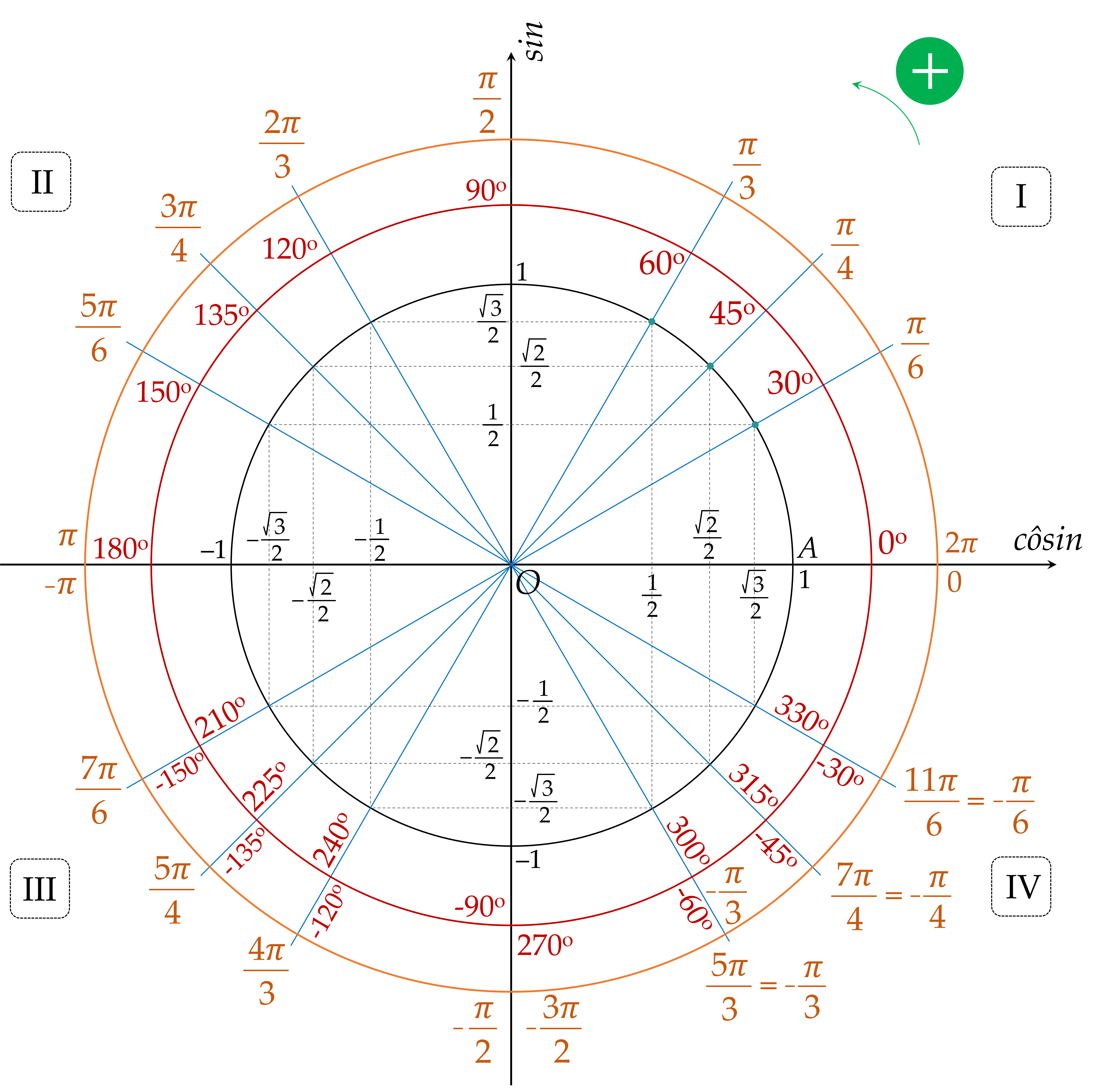
🔹Xuất phát từ điểm $M_1$ biểu diễn góc $\beta$ trên đường tròn lượng giác (vòng màu đen trong cùng) bên dưới, cộng thêm cung $\dfrac{2\pi}n$ ta được $M_2$, cứ như vậy cho đến khi đủ $n$ điểm biểu diễn $\alpha$.

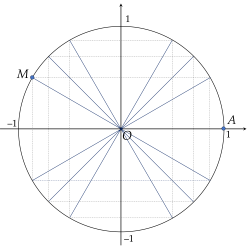
 Ví dụ 3. Điểm $M$ trong hình vẽ sau biểu diễn góc lượng giác $\dfrac{5\pi}6 + k2\pi$ với $k \in \mathbb{Z}$.

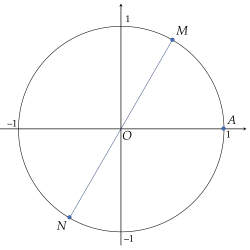
 Ví dụ 4. Xác định điểm biểu diễn góc lượng giác $\dfrac{\pi}3 + k\pi$ với $k \in \mathbb{Z}$.

Lời giải

Xét điểm $M$ là điểm biểu diễn góc $\dfrac{\pi}3$.

$\dfrac{\pi}3 + k\pi = \dfrac{\pi}3 + \dfrac{k2\pi}2$ nên có $2$ điểm biểu diễn góc lượng giác đã cho, hai điểm liên tiếp hơn kém nhau một cung có số đo $\dfrac{2\pi}2 = 180^\circ$.

 3. Độ dài cung lượng giác

🔹Cung tròn có số đo $a$ sẽ có độ dài là $l = R.a$.

🔹$2\pi=360^\circ$

Ví dụ 5. Trên đường tròn bán kính $r=5$, độ dài của cung có số đo $\dfrac{\pi }{8}$ là $l=r.a=5.\dfrac{\pi }{8}$.