Tọa độ của vectơ SVIP

1. TỌA ĐỘ CỦA VECTƠ ĐỐI VỚI MỘT HỆ TRỤC TỌA ĐỘ

a. Trục tọa độ

Trục tọa độ (gọi tắt là trục) là một đường thẳng trên đó đã xác định một điểm \(O\) (gọi là điểm gốc) và một vectơ \(\overrightarrow{e}\) có độ dài bằng \(1\) gọi là vectơ đơn vị của trục.

Ta kí hiệu trục đó là \(\left(O;\overrightarrow{e}\right).\)

b. Hệ trục tọa độ

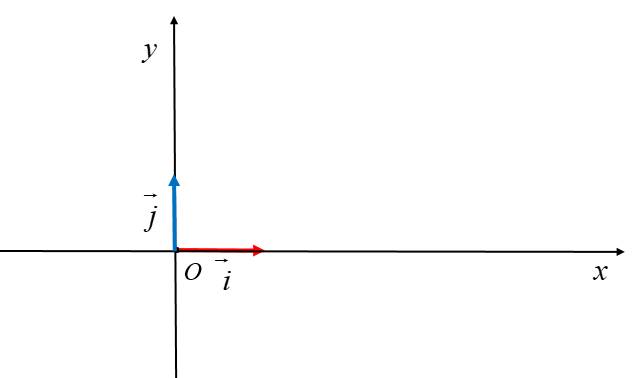
Hệ trục tọa độ \(\left(O;\overrightarrow{i},\overrightarrow{j}\right)\) gồm hai trục \(\left(O;\overrightarrow{i}\right)\) và \(\left(O;\overrightarrow{j}\right)\) vuông góc với nhau. Điểm gốc \(O\) chung của hai trục gọi là gốc tọa độ.Trục \(\left(O;\overrightarrow{i}\right)\) được gọi là trục hoành và kí hiệu là \(Ox\). Trục \(\left(O;\overrightarrow{j}\right)\) được gọi là trục tung và kí hiệu là \(Oy.\)

Các vectơ \(\overrightarrow{i},\overrightarrow{j}\) là các vectơ đơn vị trên \(Ox\) và \(Oy.\)

Hệ trục tọa độ \(\left(O;\overrightarrow{i},\overrightarrow{j}\right)\) còn được kí hiệu là \(Oxy.\)

Chú ý: Mặt phẳng mà trên đó đã cho một hệ trục tọa độ \(Oxy\) được gọi là mặt phẳng tọa độ \(Oxy\), hay gọi tắt là mặt phẳng \(Oxy.\)

c. Tọa độ của một vectơ

Trong mặt phẳng \(Oxy\), cặp số \(\left(x;y\right)\) trong biểu diễn \(\overrightarrow{a}=x\overrightarrow{i}+y\overrightarrow{j}\) được gọi là tọa độ của vectơ \(\overrightarrow{a}\), kí hiệu \(\overrightarrow{a}=\left(x;y\right)\), \(x\) gọi là hoành độ, \(y\) gọi là tung độ của vectơ \(\overrightarrow{a}.\) 

Chú ý:

• \(\overrightarrow{a}=\left(x;y\right)\Leftrightarrow\overrightarrow{a}=x\overrightarrow{i}+y\overrightarrow{j}.\)
• Nếu cho \(\overrightarrow{a}=\left(x;y\right);\overrightarrow{b}=\left(x';y'\right)\) thì \(\overrightarrow{a}=\overrightarrow{b}\Leftrightarrow\left\{{}\begin{matrix}x=x'\\y=y'\end{matrix}\right.\).

d. Tọa độ của một điểm

 Trong mặt phẳng tọa độ cho điểm \(M\) tùy ý. Tọa độ của vectơ \(\overrightarrow{OM}\) được gọi là tọa độ của điểm \(M.\)

Nhận xét:

•  Nếu \(\overrightarrow{OM}=\left(x;y\right)\) thì cặp số \(\left(x;y\right)\) là tọa độ của điểm \(M\), kí hiệu là \(M\left(x;y\right)\), \(x\) gọi là hoành độ, \(y\) gọi là tung độ của điểm \(M.\)
• \(M\left(x;y\right)\Leftrightarrow\overrightarrow{OM}=x\overrightarrow{i}+y\overrightarrow{j}.\)

Chú ý: Hoành độ và tung độ của điểm \(M\) còn được kí hiệu lần lượt là \(x_M,y_M\). Khi đó \(M\left(x_M;y_M\right).\)

Ví dụ: Trong mặt phẳng tọa độ \(Oxy\), cho điểm \(A\left(3;-4\right)\) và vectơ \(\overrightarrow{u}=\left(-2;0\right)\).

a) Biểu diễn vectơ \(\overrightarrow{OA}\) qua hai vectơ \(\overrightarrow{i}\) và \(\overrightarrow{j}\).

b) Biểu diễn vectơ \(\overrightarrow{u}\) qua hai vectơ \(\overrightarrow{i}\) và \(\overrightarrow{j}\).

Giải

a) Vì \(A\left(3;-4\right)\) nên \(\overrightarrow{OA}=\left(3;-4\right)\). Do đó: \(\overrightarrow{OA}=3\overrightarrow{i}-4\overrightarrow{j}.\) 

b) Vì \(\overrightarrow{u}=\left(-2;0\right)\) nên \(\overrightarrow{u}=\left(-2\right)\overrightarrow{i}+0\overrightarrow{j}=-2\overrightarrow{i}.\)

2. BIỂU THỨC TỌA ĐỘ CỦA CÁC PHÉP TOÁN VECTƠ

Cho hai vectơ 

 \(\overrightarrow{u}=\left(x_1;y_1\right)\) và \(\overrightarrow{v}=\left(x_2;y_2\right)\) và số thực \(k\). Khi đó:

\(\overrightarrow{u}+\overrightarrow{v}=\left(x_1+x_2;y_1+y_2\right);\)

\(\overrightarrow{u}-\overrightarrow{v}=\left(x_1-x_2;y_1-y_2\right);\)

\(k\overrightarrow{u}=\left(kx_1;ky_1\right)\);

\(\overrightarrow{u}.\overrightarrow{v}=x_1x_2+y_1y_2.\)

Ví dụ: 

Trong mặt phẳng tọa độ cho \(\overrightarrow{a}=\left(-1;2\right);\overrightarrow{b}=\left(3;1\right);\overrightarrow{c}=\left(-3;6\right)\).

a) Tìm tọa độ của vectơ \(\overrightarrow{u}=\overrightarrow{a}+2\overrightarrow{b}-\overrightarrow{c}.\)

b) Tìm tọa độ của vectơ \(\overrightarrow{x}\) sao cho \(\overrightarrow{x}+\overrightarrow{3b}=\overrightarrow{a}+2\overrightarrow{c}.\)

c) Hai vectơ \(\overrightarrow{a}\) và \(\overrightarrow{c}\) có cùng phương không? Vì sao?

Giải

a)Ta có: \(2\overrightarrow{b}=\left(6;2\right)\) do đó:

\(\overrightarrow{a}+2\overrightarrow{b}=\left(5;4\right)\Rightarrow\overrightarrow{u}=\overrightarrow{a}+2\overrightarrow{b}-\overrightarrow{c}=\left(8;-2\right).\)

b) Ta có:\(\overrightarrow{x}+\overrightarrow{3b}=\overrightarrow{a}+2\overrightarrow{c}\Rightarrow\overrightarrow{x}=\left(\overrightarrow{a}+2\overrightarrow{c}\right)-3\overrightarrow{b}\)

Trong đó \(2\overrightarrow{c}=\left(-6;12\right)\Rightarrow\overrightarrow{a}+2\overrightarrow{c}=\left(-7;14\right)\)

và \(3\overrightarrow{b}=\left(9;3\right)\)

Suy ra \(\overrightarrow{x}=\left(\overrightarrow{a}+2\overrightarrow{c}\right)-3\overrightarrow{b}=\left(-16;11\right).\)

c) Hai vectơ \(\overrightarrow{a}\) và \(\overrightarrow{c}\) cùng phương vì \(\overrightarrow{c}=2\overrightarrow{a}.\)

3. ÁP DỤNG CỦA TỌA ĐỘ VECTƠ

a. Liên hệ giữa tọa độ điểm và tọa độ vectơ trong mặt phẳng

Cho hai điểm \(A\left(x_A;y_A\right);B\left(x_B;y_B\right)\); khi đó:

\(\overrightarrow{AB}=\left(x_B-x_A;y_B-y_A\right)\).

b. Tọa độ trung điểm đoạn thẳng và trọng tâm tam giác

 Cho hai điểm \(A\left(x_A;y_A\right),B\left(x_B;y_B\right)\).

Tọa độ trung điểm \(M\left(x_M;y_M\right)\) của đoạn thẳng \(AB\) là\(x_M=\dfrac{x_A+x_B}{2};y_M=\dfrac{y_A+y_B}{2}.\)

Cho tam giác \(ABC\) có  \(A\left(x_A;y_A\right),B\left(x_B;y_B\right),C\left(x_C;y_C\right)\).

Tọa độ trọng tâm \(G\left(x_G;y_G\right)\) của tam giác \(ABC\) là:

\(x_G=\dfrac{x_A+x_B+x_C}{3};y_G=\dfrac{y_A+y_B+y_C}{3}.\)

Ví dụ: Cho tam giác \(ABC\) có \(A\left(1;5\right),B\left(-1;1\right),C\left(1;2\right)\).

a) Tìm tọa độ trung điểm \(M\) của \(AB.\)

b) Tìm tọa độ trọng tâm tam giác \(ABC.\)

Giải

a) Vì \(M\left(x_M;y_M\right)\) là trung điểm của đoạn thẳng \(AB\) nên:

\(\left\{{}\begin{matrix}x_M=\dfrac{1+\left(-1\right)}{2}\\y_M=\dfrac{5+1}{2}\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x_M=0\\y_M=3\end{matrix}\right.\)

Vậy \(M\left(0;3\right)\).

b) Vì \(G\left(x_G;y_G\right)\) là trọng tâm tam giác \(ABC\) nên

\(\left\{{}\begin{matrix}x_G=\dfrac{1+\left(-1\right)+1}{3}\\y_G=\dfrac{5+1+2}{3}\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x_G=\dfrac{1}{3}\\y_G=\dfrac{8}{3}\end{matrix}\right.\)

Vậy \(G\left(\dfrac{1}{3};\dfrac{8}{3}\right)\).

c. Ứng dụng biểu thức tọa độ của các phép toán vectơ

Cho hai vectơ \(\overrightarrow{a}=\left(a_1;a_2\right),\overrightarrow{b}=\left(b_1;b_2\right)\) và hai điểm \(A\left(x_A;y_A\right),B\left(x_B;y_B\right)\). Ta có:

\(\vec{a}\perp \vec{b}\Leftrightarrow a_{1}b_{1}+a_{2}b_{2}=0\).

\(\overrightarrow{a},\overrightarrow{b}\) cùng phương \(\Leftrightarrow a_{1}b_{2}-a_{2}b_{1}=0;\)

\(\left|\overrightarrow{a}\right|=\sqrt{a_1^2+a^2_2}\);

\(AB=\left|\overrightarrow{AB}\right|=\sqrt{\left(x_B-x_A\right)^2+\left(y_B-y_A\right)^2}\)

\(\cos\left(\overrightarrow{a},\overrightarrow{b}\right)=\dfrac{\overrightarrow{a}.\overrightarrow{b}}{\left|\overrightarrow{a}\right|.\left|\overrightarrow{b}\right|}=\dfrac{a_1b_1+a_2b_2}{\sqrt{a^2_1+a_2^2}.\sqrt{b^2_1+b_2^2}}\) (\(\overrightarrow{a},\overrightarrow{b}\) khác vectơ \(\overrightarrow{0}\))

Ví dụ: Trong mặt phẳng tọa độ \(Oxy\) cho hai điểm \(A\left(1;2\right)\) và \(B\left(5;0\right)\). 

a) Chứng minh \(OA\) vuông góc với \(AB\).

b) Gọi \(M\) là trung điểm \(AB\). Tính số đo góc \(\widehat{AOM}\).

Giải

a) Ta có \(\overrightarrow{OA}=\left(1-0;2-0\right)=\left(1;2\right)\), \(\overrightarrow{AB}=\left(5-1;0-2\right)=\left(4;-2\right)\).

Suy ra \(\overrightarrow{OA}.\overrightarrow{AB}=1.4+2.\left(-2\right)=0\).

Do các vectơ \(\overrightarrow{OA}\), \(\overrightarrow{AB}\) đều khác vectơ-không nên \(OA\perp BC\).

b) Do \(M\) là trung điểm của \(AB\) nên \(M\left(3;1\right)\). 

Suy ra \(\overrightarrow{OM}=\left(3;1\right)\), \(OM=\left|\overrightarrow{OM}\right|=\sqrt{3^2+1^2}=\sqrt{10}\).

\(\left|\overrightarrow{OA}\right|=\sqrt{1^2+2^2}=\sqrt{5}\).

Do đó \(\cos\left(\overrightarrow{OA},\overrightarrow{OM}\right)=\dfrac{\overrightarrow{OA}.\overrightarrow{OM}}{\left|\overrightarrow{OA}\right|.\left|\overrightarrow{OM}\right|}=\dfrac{1.3+2.1}{\sqrt{5}.\sqrt{10}}=\dfrac{1}{\sqrt{2}}\).

Suy ra \(0^o< \left(\overrightarrow{OA},\overrightarrow{OM}\right)< 90^o\) và do đó \(\widehat{AOM}=\left(\overrightarrow{OA},\overrightarrow{OM}\right)=45^o\) .