Báo cáo học liệu
Mua học liệu
Mua học liệu:
-
Số dư ví của bạn: 0 coin - 0 Xu
-
Nếu mua học liệu này bạn sẽ bị trừ: 2 coin\Xu
Để nhận Coin\Xu, bạn có thể:

Tính chất ba đường cao của tam giác SVIP
I. ĐƯỜNG CAO CỦA TAM GIÁC
Đoạn thẳng vuông góc kể từ một đỉnh của một tam giác đến đường thẳng chứa cạnh đối diện gọi là đường cao của tam giác đó.
Ví dụ 1. Trong hai hình dưới đây $BD$ đều là đường cao của tam giác $ABC$ ứng với cạnh $AC$.
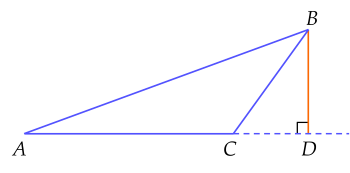
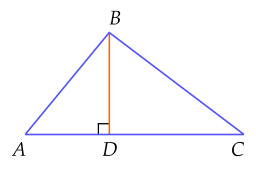
Chú ý: Mỗi tam giác có ba đường cao.
Câu hỏi:
@204420883802@@204424948778@
II. TÍNH CHẤT BA ĐƯỜNG CAO CỦA TAM GIÁC
Ba đường cao của một tam giác cùng đi qua một điểm.
Ví dụ 2. Trong hình dưới đây, ba đường cao $AD$, $BE$, $CF$ của tam giác $ABC$ cùng đi qua điểm $H$.
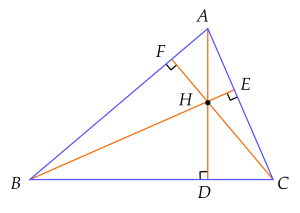
Chú ý:
⚡ Ta còn nói ba đường cao $AD$, $BE$, $CF$ đồng quy tại $H$.
⚡ Điểm $H$ được gọi là trực tâm của tam giác $ABC$.
⚡ Tam giác nhọn có trực tâm nằm bên trong tam giác.
⚡ Tam giác vuông có trực tâm trùng với đỉnh góc vuông.
⚡ Tam giác tù có trực tâm nằm ngoài tam giác.
⚡ Để xác định trực tâm của tam giác, ta chỉ cần vẽ hai đường cao bất kì và xác định giao điểm của chúng.
Ví dụ 3. Cho tam giác $LMN$ có hai đường cao $LP$ và $MQ$ cắt nhau tại $S$. Chứng minh rằng $NS$ vuông góc với $ML$.
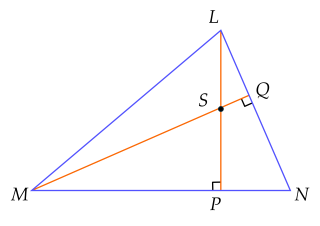
Lời giải
Tam giác $LMN$ có hai đường cao $LP$ và $MQ$ cắt nhau tại $S$ nên $S$ là trực tâm của tam giác. Do đó $NS \bot ML$.
Ví dụ 4. Cho tam giác $ABC$ có ba đường cao $AD$, $BE$, $CF$ đồng quy tại trực tâm $H$. Tìm trực tâm của các tam giác $HBC$, $HAB$, $HAC$.
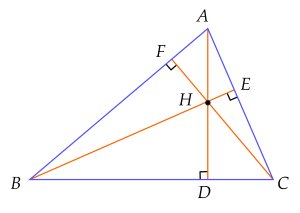
Lời giải
⚡ Tam giác $HBC$ có $HD\bot BC$, $BF\bot HC$ nên $HD$ và $BF$ là hai đường cao của tam giác $HBC$.
Mà $HD$ và $BF$ cắt nhau tại $A$ nên $A$ là trực tâm của tam giác $HBC$.
⚡ Tam giác $HAB$ có $HF\bot AB$, $BD\bot AH$ nên $HF$, $BD$ là hai đường cao của tam giác $HAB$.
Mà $HF$ và $BD$ cắt nhau tại $C$ nên $C$ là trực tâm của tam giác $HAB$.
⚡ Tam giác $HAC$ có $HE\bot AC$, $CD\bot AH$ nên $HE$, $CD$ là hai đường cao của tam giác $HAC$.
Mà $HE$ và $CD$ cắt nhau tại $B$ nên $B$ là trực tâm của tam giác $HAC$.
Câu hỏi:
@204426291451@@204426779165@
Bạn có thể đăng câu hỏi về bài học này ở đây
