olm
Đăng nhập Đăng ký Trợ giúp

Bài học cùng chủ đề

Báo cáo học liệu
Mua học liệu
Mua học liệu:
  • Số dư ví của bạn: 0 coin - 0 Xu
  • Nếu mua học liệu này bạn sẽ bị trừ: 2 coin\Xu
Thông tin của bạn

Nhận biết tiệm cận ngang, đường tiệm cận đứng, đường tiệm cận xiên của đồ thị hàm số SVIP

Câu 1 (1đ):

Cho hàm số y=f(x)y=f(x ) có đồ thị như hình vẽ.

Đường thẳng nào sau đây là tiệm cận ngang của đồ thị hàm số đã cho?

x=−1x=-1.
y=−1y=-1.
y=1y=1.
x=1x=1.
Câu 2 (1đ):

Cho hàm số y=f(x)y=f(x) xác định và có đạo hàm trên R\{±1}\mathbb{R}\backslash \{ \pm 1 \} và có bảng biến thiên như hình vẽ dưới đây:

Số tiệm cận của đồ thị hàm số đã cho là

22.
33.
11.
44.
Câu 3 (1đ):

Cho hàm số y=f(x)y=f(x) có bảng biến thiên như hình vẽ dưới đây.

Cho hàm số $y=f(x)$ có bảng biến thiên như hình vẽ

Đồ thị hàm số y=f(x)y=f(x) có bao nhiêu đường tiệm cận?

33.
22.
11.
44.
Câu 4 (1đ):

Cho hàm số y=ax+bcx+d, (ad−bc≠0;c≠0)y=\dfrac{ax+b}{cx+d},\,(ad-bc\ne 0;c\ne 0 ) có đồ thị như sau:

Tiệm cận ngang của đồ thị hàm số là đường thẳng có phương trình là

x=1x=1.
y=1y=1.
y=−1y=-1.
y=−1y=-1.
Câu 5 (1đ):

Cho hàm số y=f(x)y=f(x) xác định trên R\{−1}\mathbb{R}\backslash \{ -1 \}, liên tục trên mỗi khoảng xác định và có bảng biến thiên như sau:

Khẳng định nào dưới đây sai?

Hàm số không có đạo hàm tại x=−1x=-1.
Đồ thị hàm số không có tiệm cận đứng.
Hàm số đã cho đạt cực tiểu tại x=1x=1.
Đồ thị hàm số không có tiệm cận ngang.
Câu 6 (1đ):

Cho hàm số y=f(x)y=f\left(x \right) có bảng biến thiên như sau:

Đồ thị hàm số y=f(x)y=f\left(x \right) có bao nhiêu đường tiệm cận?

33.
00.
22.
11.
Câu 7 (1đ):

Hàm số nào sau đây có đồ thị như hình vẽ?

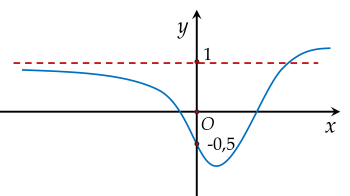
loading...

y=2x2+2x−12x2+1y=\dfrac{2{{x}^{2}}+2x-1}{2{{x}^{2}}+1}.
y=x2+2x−1x+1y=\dfrac{{{x}^{2}}+2x-1}{x+1}.
y=x2+3x−1x2+2y=\dfrac{{{x}^{2}}+3x-1}{{{x}^{2}}+2}.
y=2x2+2x−12x2−1y=\dfrac{2{{x}^{2}}+2x-1}{2{{x}^{2}}-1}.
Câu 8 (1đ):

Cho đồ thị hàm số y=f(x)y=f(x) có đồ thị như hình vẽ:

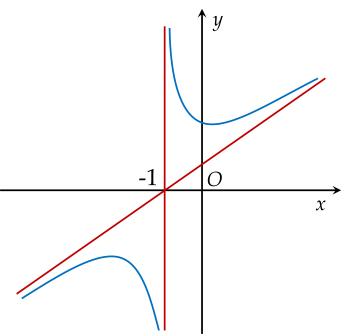
loading...

Tiệm cận đứng của đồ thị hàm số là đường thẳng

x=−1x=-1.
y=4y=4.
y=−4y=-4.
x=1x=1.
Câu 9 (1đ):

Hàm số y=f(x)y=f(x ) có đồ thị như hình vẽ:

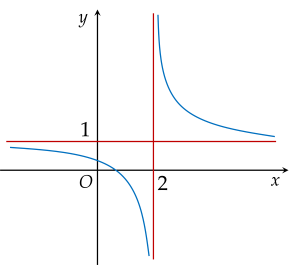
loading...

Đồ thị hàm số đã cho có tiệm cận ngang là

y=1y=1.
x=2x=2.
y=2y=2.
x=1x=1.
Câu 10 (1đ):

Cho hàm số y=f(x)y=f(x) có bảng biến thiên như hình vẽ.

Khẳng định nào dưới đây sai?

Đồ thị hàm số không có tiệm cận ngang.
Đồ thị hàm số có hai đường tiệm cận.
Đồ thị hàm số có một đường tiệm cận đứng x=0x=0.
Hàm số xác định trên R\{0}\mathbb{R}\backslash\{0\}.
Câu 11 (1đ):

Cho hàm số y=f(x)y=f(x) xác định trên R\{1;3}\mathbb{R}\backslash \{ 1;3\}, liên tục trên mỗi khoảng xác định và có bảng biến thiên như sau:

Khẳng định nào dưới đây sai?

Đường thẳng y=−1y=-1 là đường tiệm ngang của đồ thị hàm số đã cho.
Đường thẳng x=1x=1 là đường tiệm cận đứng của đồ thị hàm số đã cho.
Đường thẳng x=3x=3 là đường tiệm cận đứng của đồ thị hàm số đã cho.
Đường thẳng y=1y=1 là đường tiệm cận ngang của đồ thị hàm số đã cho.
Câu 12 (1đ):

Cho hàm số y=f(x)y=f(x) có đồ thị như hình vẽ dưới.

Tiệm cận đứng và tiệm cận ngang của đồ thị lần lượt là

x=−1x=-1 và y=2y=2.
x=1x=1 và y=2y=2.
x=−1x=-1 và y=−2y=-2.
x=1x=1 và y=−2y=-2.
Câu 13 (1đ):

Cho hàm số y=f(x)y=f(x) xác định trên R\{−1;1}\mathbb{R}\backslash \left\{ -1;1 \right\}, liên tục trên mỗi khoảng xác định và có bảng biến thiên như sau:

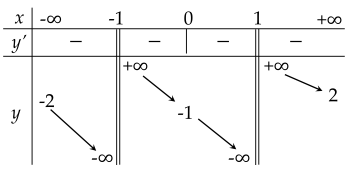
loading...

Số đường tiệm cận ngang của đồ thị hàm số y=f(x)y=f(x) là

00
44.
11.
22
Câu 14 (1đ):

Hàm số y=f(x)y=f(x) có bảng biến thiên như hình vẽ:

Khẳng định nào dưới đây đúng?

lim⁡x→−5 y=−∞\underset{x\to -5}{\mathop{\lim }}\,y=-\infty .
Đồ thị hàm số có tiệm cận ngang y=−5y=-5, tiệm cận đứng x=−1x=-1.
lim⁡x→−1− y=+∞\underset{x\to -1^-}{\mathop{\lim }}\,y=+\infty.
Hàm số xác định trên R\mathbb{R}.
Câu 15 (1đ):

Cho hàm số y=ax+bcx+dy = \dfrac{ax+b}{cx+d} với c≠0c \neq 0, ad−bc≠0ad - bc \neq 0 có đồ thị như hình vẽ:

Tiệm cận ngang của đồ thị hàm số đã cho có phương trình là

y=1y=1.
x=1x=1.
x=−1x=-1.
y=−1y=-1.
Câu 16 (1đ):

Cho hàm số y=f(x)y=f(x ) có đồ thị như hình vẽ:

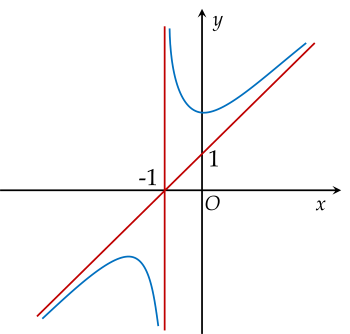
loading...

Tiệm cận xiên của đồ thị hàm số đã cho là đường thẳng

x=2x=2.
y=x−2y=x-2.
y=x−1y=x-1.
y=x+1y=x+1.
Câu 17 (1đ):

Cho hàm số y=f(x)y=f(x) có bảng biến thiên dưới đây:

(Nhấp vào ô màu vàng để chọn đúng / sai)
a) Hàm số y=f(x)y=f(x) có tập xác định là D=R\{4}D=\mathbb{R}\backslash\{4\}.
b) Đồ thị hàm số có đường tiệm cận đứng là x=5x=5.
c) Đồ thị hàm số có 22 đường tiệm cận ngang.
d) Đồ thị hàm số y=f(x)+2y=f(x)+2 không có tiệm cận ngang.
Câu 18 (1đ):

Cho hàm số y=f(x)=ax3+bx2+cx+dy=f(x)=ax^3+bx^2+cx+d, (a≠0)(a\ne 0) có đồ thị như hình vẽ bên dưới:

(Nhấp vào ô màu vàng để chọn đúng / sai)
a) Hàm số có tập xác định là R\mathbb{R}.
b) Đồ thị hàm số không có tiệm cận đứng và tiệm cận ngang.
c) Phương trình f(x)−4=0f(x)-4=0 có 33 nghiệm phân biệt.
d) Đồ thị hàm số 1f(x)−4\dfrac{1}{f(x)-4} có 11 đường tiệm cận đứng.
Câu 19 (1đ):

Cho hàm số y=f(x)=ax2+bx+cx+dy=f(x)=\dfrac{ax^2+bx+c}{x+d} có đồ thị là đường cong như hình vẽ dưới đây, biết đường tiệm xiên của đồ thị hàm số đi qua hai điểm (0;1)(0;1) và (1;0)(1;0).

hàm số $y=f(x)=\dfrac{ax^2+bx+c}{x+d}$ có đồ thị là đường cong

(Nhấp vào ô màu vàng để chọn đúng / sai)
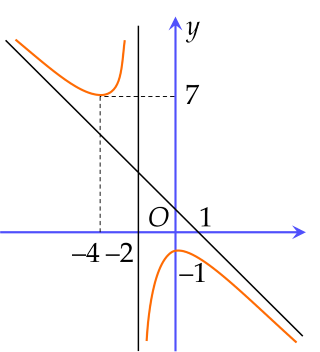
a) Khoảng cách từ M(1;−8)M(1;-8) đến đường thẳng đi qua các điểm cực trị của đồ thị hàm số bằng 5\sqrt{5}.
b) Hàm số đồng biến trên khoảng (−4;0)(-4;0).
c) Ta có a+b+c+d=−2a+b+c+d=-2.
d) Tập xác định của hàm số là R\{2}\mathbb{R}\backslash \{ 2 \}.
Câu 20 (1đ):

Cho hàm số y=f(x)y=f(x) có bảng biến thiên như sau:

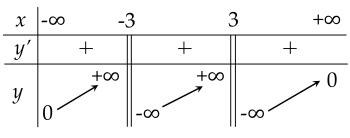
loading...

(Nhấp vào ô màu vàng để chọn đúng / sai)
a) Hàm số đã cho đồng biến trên R\mathbb{R}.
b) Phương trình y=0y=0 có 33 nghiệm phân biệt.
c) Hàm số đã cho không có cực trị.
d) Số đường tiệm cận của đồ thị hàm số là 33.
25%
Đang tải dữ liệu câu hỏi
Hôm nay, bạn còn lượt làm bài tập miễn phí. Hãy đăng nhập hoặc đăng ký và xác thực tài khoản để trải nghiệm học không giới hạn!
OLM©2022OLM \copyright 2022
Báo lỗi câu hỏi
Bạn đã gặp lỗi gì ở câu hỏi này, hãy mô tả vào ô bên dưới. Với mỗi lỗi thông báo đúng, OLM sẽ tặng bạn 1-3 ngày VIP!
Bạn có thể báo lỗi bằng hình ảnh tại đây!!!
Các khóa học có thể bạn quan tâm
Tổng thanh toán: 0đ (Tiết kiệm: 0đ)
Tới giỏ hàng
Yêu cầu VIP