Tích vô hướng của hai vectơ SVIP

1. Góc giữa hai vectơ

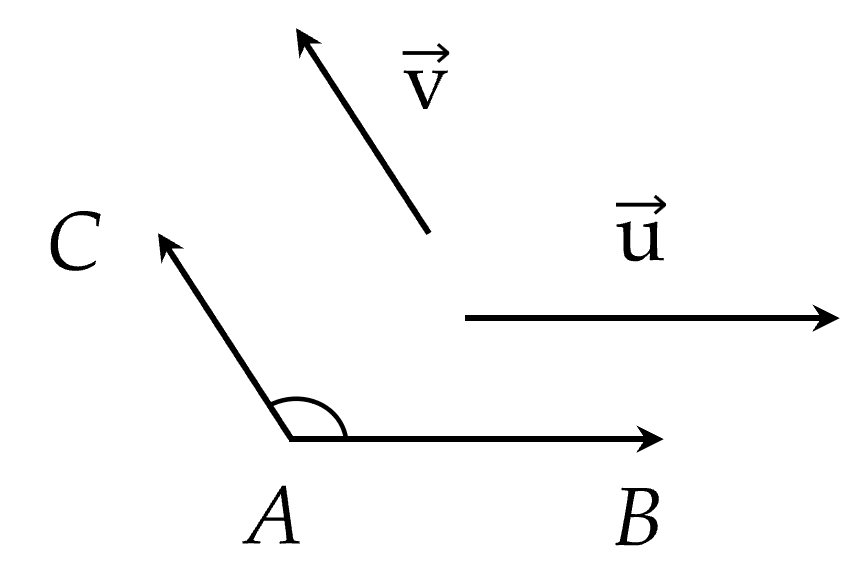
Cho hai vectơ $\vec{u}$ và $\vec{v}$ khác $\vec{0}$. Từ một điểm $A$ tuỳ ý, vẽ các vectơ $\overrightarrow{AB}=\vec{u}$ và $\overrightarrow{AC}=\vec{v}$. Khi đó số đo của góc $BAC$ được gọi là số đo góc giữa hai vectơ $\vec{u}$ và $\vec{v}$.

 Kí hiệu là $(\vec{u},\,\vec{v})$. 

​Chú ý: 

Quy ước rằng góc giữa hai vectơ $\vec{u}$ và $\vec{0}$ có thể nhận một giá trị tuỳ ý từ $0^\circ$ đến $180^\circ$.

Nếu $(\vec{u},\,\vec{v})=90^\circ$ thì ta nói rằng $\vec{u}$ và $\vec{v}$ vuông góc với nhau, kí hiệu là $\vec{u}\perp\vec{v}$ hoặc $\vec{v}\perp\vec{u}$. Đặc biệt, $\vec{0}$ được coi là vuông góc với mọi vectơ.

Ví dụ 1: Cho tam giác $ABC$ vuông tại $A$ và $\widehat{B}=30^\circ$. Tính $(\overrightarrow{AB},\,\overrightarrow{AC})$, $(\overrightarrow{CA},\,\overrightarrow{CB})$, $(\overrightarrow{AB},\,\overrightarrow{BC})$.

Lời giải

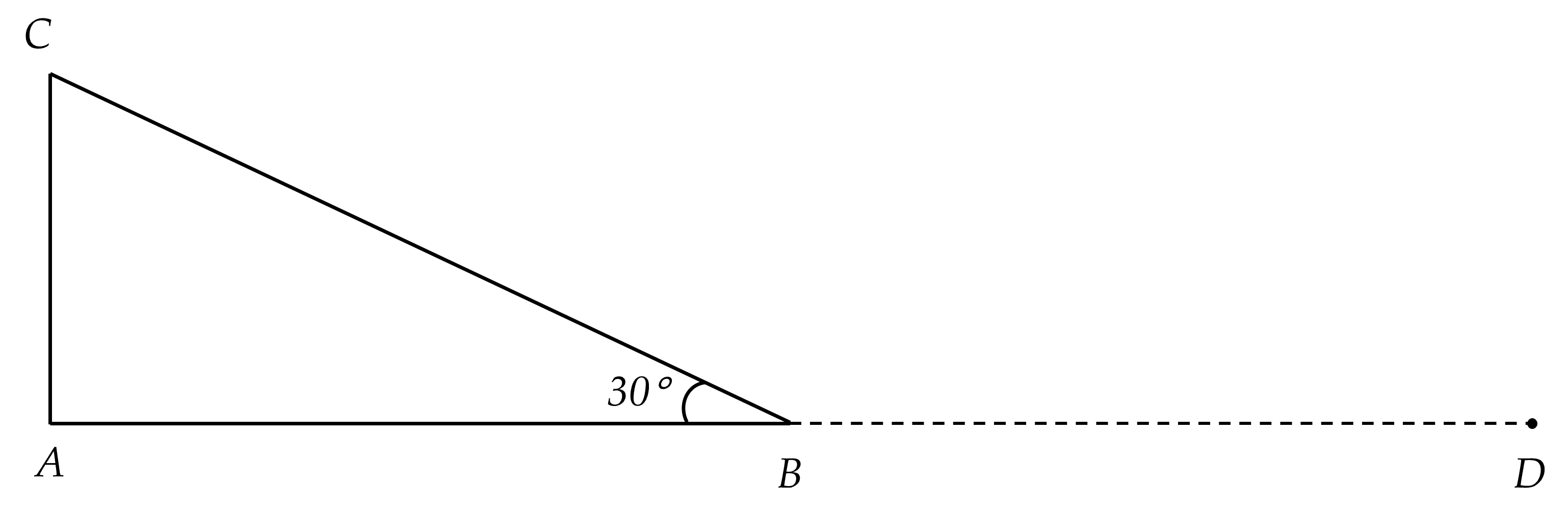
 Ta có $(\overrightarrow{AB},\,\overrightarrow{AC})=\widehat{BAC}=90^\circ$, $(\overrightarrow{CA},\,\overrightarrow{CB}) = \widehat{ACB}=60^\circ$,

$(\overrightarrow{AB},\,\overrightarrow{BC}) =(\overrightarrow{BD},\,\overrightarrow{BC})= \widehat{DBC}=150^\circ $.

2. Tích vô hướng của hai vectơ

Tích vô hướng của hai vectơ $\vec{u}$ và $\vec{v}$ là một số, kí hiệu là $\vec{u}.\vec{v}$ được xác định bởi công thức sau:

$\vec{u}.\vec{v}=$$ |\vec{u}|.|\vec{v}|.\cos (\vec{u},\,\vec{v})$.

Chú ý:

$\vec{u} \perp \vec{v} \Leftrightarrow\vec{u}.\vec{v}=0$.

$\vec{u}.\vec{u}$ còn được viết là $\vec{u}^2$ và được gọi là bình phương vô hướng của vectơ $\vec{u}$.

Ta có $\vec{u}^2=|\vec{u}|.|\vec{u}|.\cos 0^\circ = |\vec{u}|^2$.

3. Biểu thức toạ độ và tính chất của tích vô hướng

Biểu thức toạ độ

Tích vô hướng của hai vectơ $\vec{u}=(x;\,y)$ và $\vec{v}=(x';\,y')$ được tính theo công thức:

$\vec{u}.\vec{v}=xx'+yy'$.

Nhận xét:

Hai vectơ $\vec{u}$ và $\vec{v}$ vuông góc với nhau khi và chỉ khi $xx'+yy'=0$.

Bình phương vô hướng của $\vec{u}(x;\,y)$ là $\vec{u}^2=x^2+y^2$.

Nếu $\vec{u}\ne\vec{0}$ và $\vec{v}\ne\vec{0}$ thì $\cos (\vec{u},\,\vec{v}) = \dfrac{\vec{u}.\vec{v}}{|\vec{u}|.|\vec{v}|}=\dfrac{xx'+yy'}{\sqrt{x^2+y^2}+\sqrt{x'^2+y'^2}}$.

Tính chất của tích vô hướng 

Với ba vectơ $\vec{u},\,\vec{v},\,\vec{w}$ bất kì và mọi số thực $k$, ta có

$\vec{u}.\vec{v}=\vec{v}.\vec{u}$

$\vec{u}.(\vec{v}+\vec{w})=\vec{u}.\vec{v}+\vec{u}.\vec{w}$

$(k.\vec{u}).\vec{v}=k.(\vec{u}.\vec{v})=\vec{u}.(k.\vec{v})$

Ví dụ 2: Tính tích vô hướng và góc giữa hai vectơ $\vec{u}(0;\,-5)$ và $\vec{v}(\sqrt{3};\,1)$ .

Lời giải

Tích vô hướng của hai vectơ: $\vec{u}.\vec{v}=0.\sqrt{3}+(-5).1=-5.$

Ta có $\cos (\vec{u},\,\vec{v})=\dfrac{\vec{u}.\vec{v}}{|\vec{u}|.|\vec{v}|}=\dfrac{-5}{\sqrt{0^2+(-5)^2}.\sqrt{(\sqrt{3})^2+1^2}}=-\dfrac{1}{2}$.

$\Rightarrow (\vec{u},\,\vec{v}) = 120^\circ$.