Bài học cùng chủ đề
- Tỉ số lượng giác của góc nhọn (Phần 1)
- Tỉ số lượng giác của góc nhọn (Phần 2)
- Bài tập: Tỉ số lượng giác của góc nhọn (Phần 1)
- Bài tập: Tỉ số lượng giác của góc nhọn (Phần 2)
- Tỉ số lượng giác của góc nhọn
- Tỉ số lượng giác của góc nhọn
- Tính các giá trị lượng giác. Chứng minh/đơn giản các hệ thức lượng giác
- Phiếu bài tập
Báo cáo học liệu
Mua học liệu
Mua học liệu:
-
Số dư ví của bạn: 0 coin - 0 Xu
-
Nếu mua học liệu này bạn sẽ bị trừ: 2 coin\Xu
Để nhận Coin\Xu, bạn có thể:

Tỉ số lượng giác của góc nhọn SVIP
1. Khái niệm tỉ số lượng giác của một góc nhọn
a) Mở đầu
Cho tam giác $ABC$ vuông tại $A$. Xét góc nhọn $B$ của nó.
Nhắc lại rằng:
+) Cạnh $AB$ được gọi là cạnh kề của góc $B$.
+) Cạnh $AC$ được gọi là cạnh đối của góc $B$.
Khi đó, tỉ số giữa cạnh đối và cạnh kề của một góc nhọn trong tam giác vuông đặc trưng cho độ lớn của góc nhọn đó.
b) Định nghĩa
Cho góc nhọn $\alpha$. Vẽ một tam giác vuông có một góc nhọn $\alpha$ (như hình vẽ). Khi đó:
|
$\sin\alpha=\dfrac{\text{cạnh đối}}{\text{cạnh huyền}}$; $\tan\alpha=\dfrac{\text{cạnh đối}}{\text{cạnh kề}}$; |
$\cos\alpha=\dfrac{\text{cạnh kề}}{\text{cạnh huyền}}$; $\cot\alpha=\dfrac{\text{cạnh kề}}{\text{cạnh đối}}$. |
.svg) |
Nhận xét. Từ định nghĩa trên, ta thấy tỉ số lượng giác của một góc nhọn luôn dương và $\sin\alpha<1$, $\cos \alpha <1$.
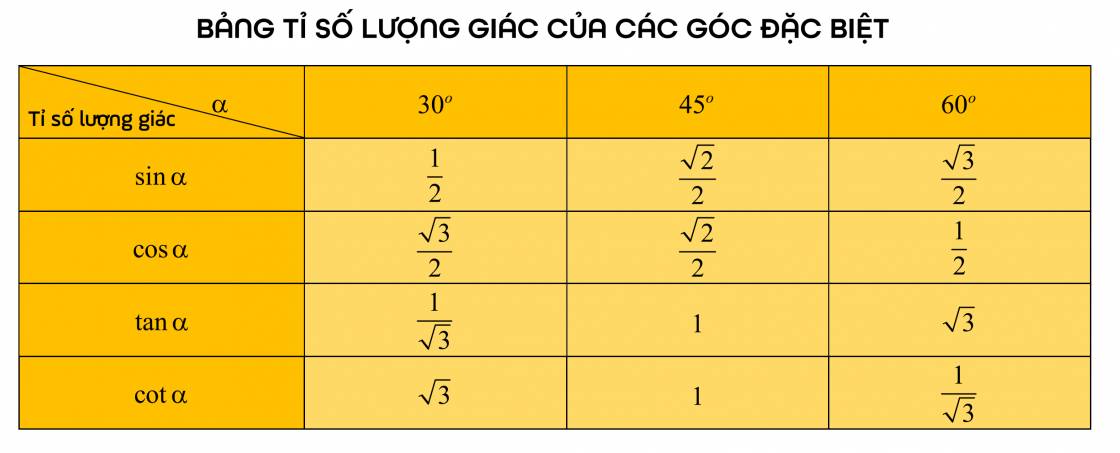
2. Tỉ số lượng giác của hai góc phụ nhau
Tương tự như bài trên, ta rút ra định lý sau:
Định lý
Hay
Trong tam giác $ABC$ vuông tại $A$, ta có:
$\sin B=\cos C$; $\cos B=\sin C$;
$\tan B=\cot C$; $\cot B=\tan C$.
Bạn có thể đăng câu hỏi về bài học này ở đây

