Tỉ số lượng giác của các góc nhọn đặc biệt SVIP

Nối.

Nối.

Giá trị của biểu thức $B = \tan 45^\circ . \cos 30^\circ . \cot 30^\circ$ là

Giá trị của biểu thức $A = \dfrac{2 \cos 45^\circ}{\sqrt2} + \sqrt{3} \tan 30^\circ$ là

Giá trị của biểu thức $A = 4 - \sin^2 45^\circ + 2 \cos^2 60^\circ - 3 \cot^3 45^\circ$ là

Cho góc nhọn $\beta$ thỏa mãn $\sin \beta = \cos \beta$ và $\sin^2 \beta + \cos^2 \beta = 1$. Số đo góc $\beta$ là

Cho tam giác $ABC$ vuông cân tại $A$. Tỉ số lượng giác sin, côsin, tang của góc $B$ lần lượt là

Cho tam giác $ABC$ vuông tại $A$ có $\widehat C = 45^\circ$ và $AB = c$. Độ dài cạnh $BC$ tính theo $c$ là

Cho tam giác vuông có một góc nhọn $60^\circ$ và cạnh kề với góc $60^\circ$ bằng $3$ cm. Cạnh đối của góc này có độ dài là

Cho tam giác vuông có một góc nhọn bằng $30^\circ$ và cạnh đối với góc này bằng $8$ m. Độ dài cạnh huyền của tam giác là

Cho tam giác $ABC$ cân tại $A$, đường cao $AH$ như hình vẽ.

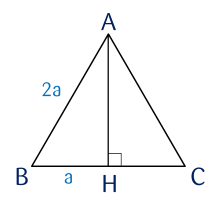
Biết rằng trong tam giác vuông, cạnh đối diện với góc $30^\circ$ bằng nửa cạnh huyền. Tỉ số lượng giác sin và tang của góc $BAH$ lần lượt là