Quan hệ giữa góc và cạnh đối diện trong tam giác SVIP

I. GÓC ĐỐI DIỆN VỚI CẠNH LỚN HƠN TRONG TAM GIÁC

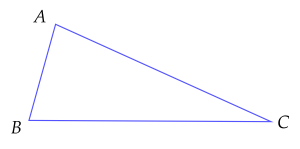
Cho tam giác $ABC$, góc $A$ đối diện với cạnh $BC$, góc $B$ đối diện với cạnh $AC$, góc $C$ đối diện với cạnh $AB$.

Trong một tam giác, góc đối diện với cạnh lớn hơn là góc lớn hơn.

Ví dụ 1. Cho tam giác $ABC$ có $AB=3$ cm, $BC=5$ cm, $CA=7$ cm.

Hãy so sánh các góc của tam giác $ABC$.

Lời giải

Trong tam giác $ABC$, ta thấy $ AB<BC<AC $ do đó theo định lí 1 ta có $ \widehat{C}<\widehat{A}<\widehat{B} $.

II. CẠNH ĐỐI DIỆN VỚI GÓC LỚN HƠN TRONG MỘT TAM GIÁC

Trong một tam giác, cạnh đối diện với góc lớn hơn là cạnh lớn hơn.

Ví dụ 2. Cho tam giác $MNP$ có $ \widehat{N}=70^\circ;\,\widehat{P}=50 ^\circ$. Hãy so sánh độ dài các cạnh của tam giác.

Lời giải

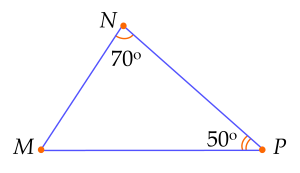
Trong tam giác $MNP$ có $ \widehat{N}=70^\circ;\,\widehat{P}=50 ^\circ$ nên:

$ \widehat{M}=180^\circ-(\widehat{N}+\widehat{P})=180^\circ-(70^\circ+50^\circ)=60$. (tổng ba góc trong một tam giác bằng $180^\circ$)

Trong tam giác $MNP$ có $ \widehat{P}<\widehat{M}<\widehat{N}$

suy ra $ MN<NP<MP $ (định lí 2).

Nhận xét:

⚡ Trong tam giác vuông, góc vuông là góc lớn nhất nên cạnh đối diện với góc vuông (tức là cạnh huyền) là cạnh lớn nhất.

⚡ Tương tự trong tam giác tù, cạnh đối diện với góc tù là cạnh lớn nhất.

Ví dụ 3.

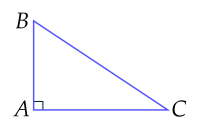
a) Cho tam giác $ABC$ vuông tại $A$, khi đó cạnh $BC$ là cạnh lớn nhất.

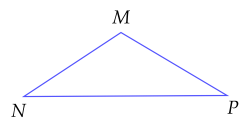
b) Cho tam giác $MNP$ có góc $M>90^\circ$, khi đó cạnh $NP$ là cạnh lớn nhất.

Ví dụ 4. Ba bạn Mai, Việt và Hà đi đến trường tại địa điểm $D$ lần lượt theo ba con đường $AD, BD$ và $CD$. Biết rằng ba điểm $A,\,B,\,C$ cùng nằm trên một đường thẳng, $B$ nằm giữa $A$ và $C$, $\widehat{ACD}$ là góc tù. Bạn nào đi xa nhất, bạn nào đi gần nhất? Vì sao?

Lời giải

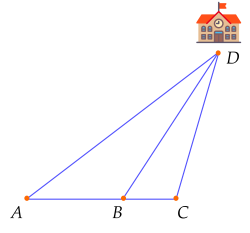
Ta có $\widehat{ABD}$ là góc ngoài tại đỉnh $B$ của $\Delta BCD$ nên $\widehat{ABD}=\widehat{BDC}+\widehat{BCD}>\widehat{BCD}$.

Do đó $\widehat{ABD}$ là góc tù.

⚡Xét $\Delta ABD$ có $\widehat{ABD}$ là góc tù nên $\widehat{ABD}$ là góc lớn nhất trong tam giác.

Cạnh đối diện với $\widehat{ABD}$ trong $\Delta ABD$ là cạnh $AD$.

Do đó cạnh $AD$ là cạnh lớn nhất trong $\Delta ABD$.

Khi đó $AD > BD$ (1).

⚡Xét $\Delta BCD$ có $\widehat{BCD}$ là góc tù nên $\widehat{BCD}$ là góc lớn nhất trong tam giác.

Cạnh đối diện với $\widehat{BCD}$ trong $\Delta BCD$ là cạnh $BD$.

Do đó cạnh $BD$ là cạnh lớn nhất trong $\Delta BCD$.

Khi đó $BD > CD$ (2).

Từ (1) và (2) suy ra $AD > BD > CD$.

Vậy bạn Mai đi xa nhất, bạn Hà đi gần nhất.