Bài học cùng chủ đề
- Phương trình và hệ phương trình bậc nhất hai ẩn
- Khái niệm phương trình bậc nhất hai ẩn
- Viết nghiệm và biểu diễn hình học các nghiệm của phương trình bậc nhất hai ẩn
- Hệ hai phương trình bậc nhất hai ẩn
- Nhận diện phương trình và hệ hai phương trình bậc nhất hai ẩn và kiểm tra nghiệm
- Viết nghiệm và biểu diễn hình học các nghiệm của phương trình bậc nhất hai ẩn
- Ứng dụng thực tế của phương trình bậc nhất hai ẩn, hệ hai phương trình bậc nhất hai ẩn
- Phiếu bài tập tuần 1. Phương trình và hệ hai phương trình bậc nhất hai ẩn
Báo cáo học liệu
Mua học liệu
Mua học liệu:
-
Số dư ví của bạn: 0 coin - 0 Xu
-
Nếu mua học liệu này bạn sẽ bị trừ: 2 coin\Xu
Để nhận Coin\Xu, bạn có thể:

Phương trình và hệ phương trình bậc nhất hai ẩn SVIP
1. PHƯƠNG TRÌNH BẬC NHẤT HAI ẨN
Định nghĩa
Phương trình bậc nhất hai ẩn $x$, $y$ là hệ thức dạng: $ax + by = c$, trong đó $a$, $b$, $c$ là những số cho trước, $a \ne 0$ hoặc $b \ne 0$.
Ví dụ 1. Phương trình nào sau đây là phương trình bậc nhất hai ẩn?
+ Phương trình bậc nhất hai ẩn $x$, $y$: $2x - y = 1$; $0x + 3y = 9$ và $5x + 0y = -2$.
+ $3x^2 - y = 7$ và $0x + 0y = 1$ không phải phương trình bậc nhất hai ẩn.
Nghiệm của phương trình bậc nhất hai ẩn
Cho phương trình bậc nhất hai ẩn $x$, $y$: $ax + by = c$. Nếu $ax_0 + by_0 = c$ là một khẳng định đúng thì cặp số $(x_0 ; y_0)$ được gọi là một nghiệm của phương trình $ax + by = c$.
Ví dụ 2. Cho phương trình bậc nhất hai ẩn: $2x + 3y = 5$.
Cặp số $(1 ; 1)$ là một nghiệm của phương trình trên vì: $VT = 2.1 + 3.1 = 5 = VP$.
Chú ý: Mỗi phương trình bậc nhất hai ẩn đều có vô số nghiệm.
Nghiệm tổng quát và biểu diễn hình học
⚡Mỗi nghiệm của phương trình $ax + 0y = c$ ($a \ne 0$) được biểu diễn bởi điểm có toạ độ $\Big(\dfrac ca ; y_0\Big)$ nằm trên đường thẳng $d_1$: $x = \dfrac ca$.
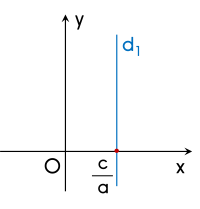
Đường thẳng $d_1$ là đường thẳng đi qua điểm $\dfrac ca$ trên trục $Ox$ và vuông góc với trục $Ox$.
⚡Mỗi nghiệm của phương trình $0x + by = c$ ($b \ne 0$) được biểu diễn bởi điểm có toạ độ $\Big(x_0 ; \dfrac cb\Big)$ nằm trên đường thẳng $d_2$: $x = \dfrac cb$.
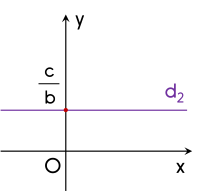
Đường thẳng $d_2$ là đường thẳng đi qua điểm $\dfrac cb$ trên trục $Oy$ và vuông góc với trục $Oy$.
⚡Mỗi nghiệm của phương trình $ax + by = c$ (với $a \ne 0$; $b \ne 0$) được biểu diễn bởi điểm nằm trên đường thẳng $d_3$: $y = -\dfrac abx + \dfrac cb$.
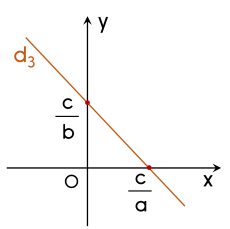
Đường thẳng $d_3$ là đồ thị của hàm số: $y = -\dfrac abx + \dfrac cb$.
2. HỆ HAI PHƯƠNG TRÌNH BẬC NHẤT HAI ẨN
Khái niệm
Hệ hai phương trình bậc nhất hai ẩn có dạng: $\left\{\begin{aligned}&ax + by = c\\&a'x + b'y = c'\\ \end{aligned}\right.$ (I), ở đó mỗi phương trình $ax + by = c$ và $a'x + b'y = c'$ đều là phương trình bậc nhất hai ẩn.
Ví dụ 3. Hệ hai phương trình bậc nhất hai ẩn: $\left\{\begin{aligned}&5x + 3y = 39\\&6x + 2y = 42\\ \end{aligned}\right.$.
Nghiệm của hệ hai phương trình bậc nhất hai ẩn
Xét hệ hai phương trình bậc nhất hai ẩn: $\left\{\begin{aligned}&ax + by = c\\&a'x + b'y = c'\\ \end{aligned}\right.$ (I)
+ Nếu cặp số $(x_0 ; y_0)$ là nghiệm của từng phương trình trong hệ (I) thì cặp số $(x_0 ; y_0)$ được gọi là nghiệm của hệ (I).
+ Giải hệ phương trình là tìm tất cả nghiệm của hệ phương trình đó.
Bạn có thể đăng câu hỏi về bài học này ở đây
