Bài học cùng chủ đề
- Phương trình đường thẳng
- Phương trình tổng quát của đường thẳng
- Phương trình tham số của đường thẳng
- Vectơ chỉ phương và vectơ pháp tuyến của đường thẳng
- Viết phương trình đường thẳng
- Phương trình tham số của đường thẳng
- Phương trình tổng quát của đường thẳng (phần 1)
- Phương trình tổng quát của đường thẳng (phần 2)
- Phiếu bài tập: Xác định các yếu tố của đường thẳng
Báo cáo học liệu
Mua học liệu
Mua học liệu:
-
Số dư ví của bạn: 0 coin - 0 Xu
-
Nếu mua học liệu này bạn sẽ bị trừ: 2 coin\Xu
Để nhận Coin\Xu, bạn có thể:

Phương trình đường thẳng SVIP
1. PHƯƠNG TRÌNH TỔNG QUÁT CỦA ĐƯỜNG THẲNG
Vectơ \(\overrightarrow{n}\) khác \(\overrightarrow{0}\) được gọi là vectơ pháp tuyến của đường thẳng \(\Delta\) nếu giá của nó vuông góc với \(\Delta\).
Trong mặt phẳng tọa độ, mọi đường thẳng đều có phương trình tổng quát dạng \(ax+by+c=0\), với \(a\) và \(b\) không đồng thời bằng \(0\).
Phương trình đường thẳng đi qua \(M\left(x_0;y_0\right)\) và nhận vectơ \(\overrightarrow{n}\left(a;b\right)\) là vectơ pháp tuyến có dạng \(a\left(x-x_0\right)+b\left(y-y_0\right)=0\) hay \(ax+by-ax_0-by_0=0\).
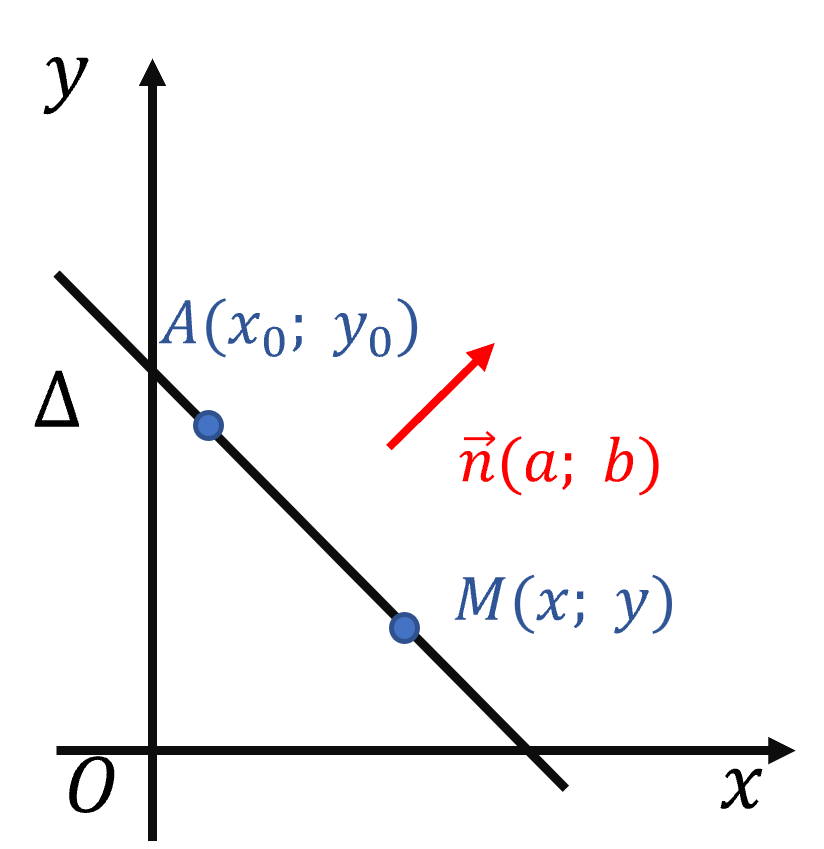
Mỗi phương trình dạng \(ax+by+c=0\) (\(a\) và \(b\) không đồng thời bằng \(0\)) đều là phương trình tổng quát của một đường thẳng, nhận \(\overrightarrow{n}\left(a;b\right)\) là vectơ pháp tuyến.
2. PHƯƠNG TRÌNH THAM SỐ CỦA ĐƯỜNG THẲNG
Vectơ \(\overrightarrow{u}\) khác \(\overrightarrow{0}\) được gọi là vectơ chỉ phương của đường thẳng \(\Delta\) nếu giá của nó song song hoặc trùng với \(\Delta\).
Nếu \(\overrightarrow{n}\left(a;b\right)\) là một vectơ pháp tuyến của \(\Delta\) thì \(\overrightarrow{u}\left(-b;a\right)\) và \(\overrightarrow{v}\left(b;-a\right)\) là các vectơ chỉ phương của \(\Delta\).
Nếu \(\overrightarrow{u}\left(a;b\right)\) là một vectơ chỉ phương của \(\Delta\) thì \(\overrightarrow{n_1}\left(-b;a\right)\) và \(\overrightarrow{n_2}\left(b;-a\right)\) là các vectơ pháp tuyến của \(\Delta\).
Đường thẳng \(\Delta\) đi qua điểm \(M\left(x_0;y_0\right)\) và nhận \(\overrightarrow{u}\left(a;b\right)\) là vectơ chỉ phương. Khi đó phương trình tham số của đường thẳng \(\Delta\) là \(\left\{{}\begin{matrix}x=x_0+at\\y=y_0+bt.\end{matrix}\right.\)
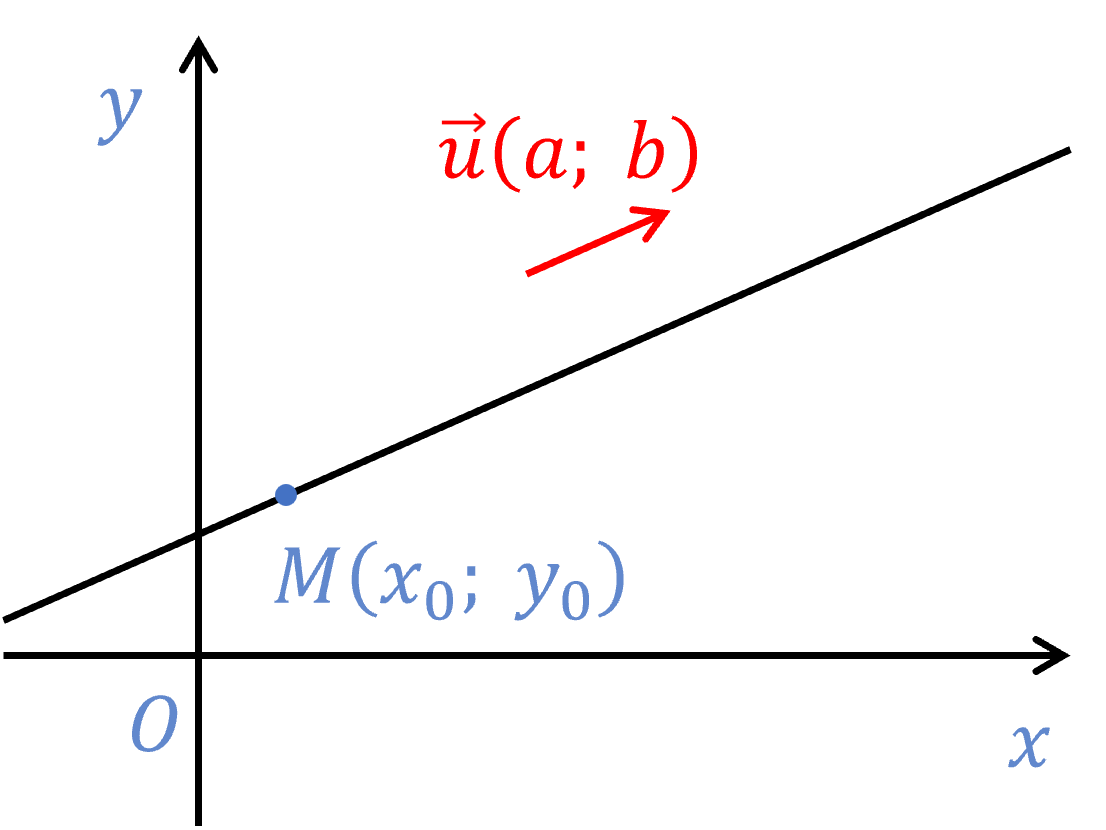
Ví dụ: Trong mặt phẳng \(Oxy\), cho điểm \(A\left(2;3\right)\) và hai vectơ \(\overrightarrow{u}=\left(1;2\right)\), \(\overrightarrow{n}=\left(-2;1\right)\).
a) Lập phương trình tổng quát của đường thẳng \(A\) và nhận \(\overrightarrow{n}\) là vectơ pháp tuyến.
b) Lập phương trình tham số của đường thẳng đi qua \(A\) và nhận \(\overrightarrow{u}\) là vectơ chỉ phương.
c) Lập phương trình tổng quát và phương trình tham số của đường thẳng đi qua điểm \(A\) và điểm \(B\left(3;2\right)\).
Giải:
a) Phương trình tổng quát của đường thẳng cần tìm là
\(-2\left(x-2\right)+1\left(y-3\right)=0\Leftrightarrow-2x+y+1=0\).
b) Phương trình tham số của đường thẳng cần tìm là
\(\left\{{}\begin{matrix}x=2+t\\y=3+2t.\end{matrix}\right.\)
c) Đường thẳng \(AB\) nhận \(\overrightarrow{AB}\) là một vectơ chỉ phương.
\(\overrightarrow{AB}=\left(3-2;2-3\right)=\left(1;-1\right)\).
Phương trình tham số của đường thẳng \(AB\) là
\(\left\{{}\begin{matrix}x=2+t\\y=3-t.\end{matrix}\right.\)
Do \(\overrightarrow{AB}=\left(1;-1\right)\) là một vectơ chỉ phương của đường thẳng \(AB\) nên \(\overrightarrow{n_{AB}}=\left(1;1\right)\) là một vectơ pháp tuyến của đường thẳng \(AB\).
Phương trình tổng quát của đường thẳng \(AB\) là
\(1\left(x-2\right)+1\left(y-3\right)=0\Leftrightarrow x+y-5=0\).
Bạn có thể đăng câu hỏi về bài học này ở đây
