Báo cáo học liệu
Mua học liệu
Mua học liệu:
-
Số dư ví của bạn: 0 coin - 0 Xu
-
Nếu mua học liệu này bạn sẽ bị trừ: 2 coin\Xu
Để nhận Coin\Xu, bạn có thể:

Phương trình dao động điều hòa SVIP
I. LI ĐỘ TRONG DAO ĐỘNG ĐIỀU HÒA
➤ Phương trình li độ của vật dao động
Phương trình li độ của vật dao động điều hòa có dạng:
\(x=A\cos\left(\omega t+\varphi_0\right)\)
Trong đó:
- $x$, $A$ lần lượt là li độ và biên độ dao động của vật, có đơn vị là m.
- \(\omega\) là tần số góc của dao động, có đơn vị là rad/s.
- \(\varphi=\omega t+\varphi_0\) là pha của dao động tại thời điểm $t$, có đơn vị là rad.
- \(\varphi_0\) là pha ban đầu của dao động, có đơn vị là rad.
➤ Độ dịch chuyển của vật dao động
Tại một thời điểm bất kì, độ dịch chuyển của vật dao động so với vị trí ban đầu được xác định bằng công thức:
\(d=\Delta x=x-x_0=Acos\left(\omega t+\varphi_0\right)-Acos\varphi_0\)
Nhận xét:
- Độ dịch chuyển so với vị trí ban đầu của vật cũng biến thiên điều hòa theo thời gian cùng biên độ, chu kì và pha với li độ của vật dao động.
- Tại từng thời điểm, đồ thị độ dịch chuyển - thời gian dịch xuống một đoạn \(Acos\varphi_0\) trên trục tung so với đồ thị li độ - thời gian.
- $d$ trùng với $x$ khi gốc thời gian được chọn lúc vật đi qua vị trí cân bằng \(\left(cos\varphi_0=0\right)\).
II. VẬN TỐC TRONG DAO ĐỘNG ĐIỀU HÒA
➤ Phương trình vận tốc của vật dao động
Vận tốc tức thời của một vật được xác định bằng công thức: \(\text{v}=\dfrac{\Delta x}{\Delta t}\) với \(\Delta t\) rất nhỏ, tức là bằng độ dốc của đồ thị (\(x\) - \(t\)) tại điểm đang xét.
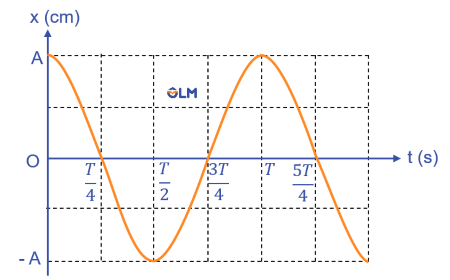
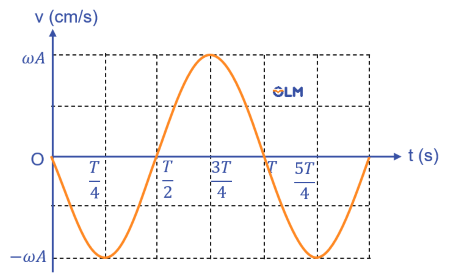
Nhận xét:
- Đồ thị vận tốc - thời gian của vật dao động điều hòa cũng có dạng hình sin. Nghĩa là vận tốc của vật dao động điều hòa cũng biến đổi điều hòa theo thời gian.
- Vận tốc và li độ của vật dao động điều hòa có cùng chu kì $T$ (cùng tần số $f$).
- Tỉ số của tốc độ cực đại và biên độ dao động của vật bằng \(\omega\). Nghĩa là \(v_{max}=\omega A.\)
- Vận tốc biến đổi điều hòa theo thời gian lệch pha \(\dfrac{\pi}{2}\) so với li độ.
➤ Phương trình vận tốc của vật dao động điều hòa
Phương trình vận tốc của vật dao động điều hòa có dạng:
\(v=\omega Acos\left(\omega t+\varphi_0+\dfrac{\pi}{2}\right)=-\omega Asin\left(\omega t+\varphi_0\right)\)
III. GIA TỐC TRONG DAO ĐỘNG ĐIỀU HÒA
➤ Phương trình gia tốc của vật dao động
Gia tốc tức thời của một vật được xác định bằng công thức: \(a=\dfrac{\Delta\text{v}}{\Delta t}\) với \(\Delta t\) rất nhỏ, tức là bằng độ dốc của đồ thị vận tốc tại điểm đang xét.
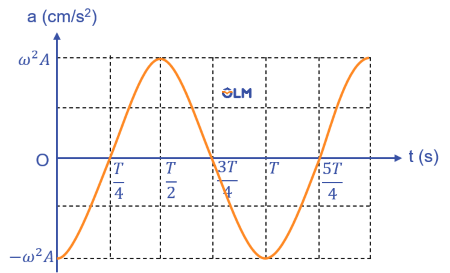
Nhận xét:
- Đồ thị gia tốc - thời gian của vật dao động điều hòa có dạng hình sin.
- Gia tốc và li độ của vật dao động điều hòa có cùng chu kì $T$ (cùng tần số $f$).
- Tỉ số của độ lớn cực đại của gia tốc và biên độ dao động của vật bằng \(\omega^2\). Nghĩa là \(a_{max}=\omega^2A.\)
- Gia tốc và li độ của vật luôn lệch pha \(\pi\) so với nhau (ngược pha nhau).
Phương trình gia tốc của vật dao động điều hòa có dạng:
\(a=\omega^2Acos\left(\omega t+\varphi_0+\pi\right)\\ =-\omega^2Acos\left(\omega t+\varphi_0\right)=-\omega^2x\)
1. Phương trình li độ của vật dao động điều hòa có dạng:
\(x=Acos\left(\omega t+\varphi_0\right)\)
2. Phương trình vận tốc của vật dao động điều hòa có dạng:
\(v=\omega Acos\left(\omega t+\varphi_0+\dfrac{\pi}{2}\right)=-\omega Asin\left(\omega t+\varphi_0\right)\)
3. Phương trình gia tốc của vật dao động điều hòa có dạng:
\(a=\omega^2Acos\left(\omega t+\varphi_0+\pi\right)\\ =-\omega^2Acos\left(\omega t+\varphi_0\right)=-\omega^2x\)
Bạn có thể đăng câu hỏi về bài học này ở đây
