Bài học cùng chủ đề
- Căn bậc hai và căn thức bậc hai
- Căn bậc hai
- Căn thức bậc hai
- Căn bậc hai của một số, biểu thức số
- Điều kiện xác định của căn thức bậc hai
- Tính, rút gọn biểu thức số dạng $\sqrt{A^2}$
- Tính, rút gọn căn thức bậc hai
- So sánh, tìm giá trị chưa biết trong biểu thức chứa căn thức bậc hai
- Phiếu bài tập: Căn bậc hai, căn thức bậc hai
Báo cáo học liệu
Mua học liệu
Mua học liệu:
-
Số dư ví của bạn: 0 coin - 0 Xu
-
Nếu mua học liệu này bạn sẽ bị trừ: 2 coin\Xu
Để nhận Coin\Xu, bạn có thể:

Phiếu bài tập: Căn bậc hai, căn thức bậc hai SVIP
Yêu cầu đăng nhập!
Bạn chưa đăng nhập. Hãy đăng nhập để làm bài thi tại đây!
Giá trị của x để các căn thức −3x có nghĩa là
Căn bậc hai số học của 169 là
Số x không âm thỏa mãn x=5 là
Giá trị của biểu thức L=2194−521625 bằng
Trong một thí nghiệm, một vật rơi tự do từ độ cao 80 (m) so với mặt đất. Biết quãng đường dịch chuyển được của vật đó tính theo đơn vị mét được cho bởi công thức h=5t2 với t là thời gian vật đó rơi, tính theo đơn vị giây (t>0). Sau bao nhiêu giây kể từ lúc rơi thì vật đó chạm đất?
Trả lời:
Rút gọn biểu thức xx6 khi x<0 ta được
Để lái xe an toàn khi đi qua đoạn đường có dạng cung tròn, người lái cần biết tốc độ tối đa cho phép là bao nhiêu. Vì thế, ở những đoạn đường đó thường có bảng chỉ dẫn cho tốc độ tối đa cho phép của ô tô. Tốc độ tối đa cho phép v (m/s) được tính bởi công thức v=rgu, trong đó r (m) là bán kính của cung đường, g=9,8 m/s2, u=0,12 là hệ số ma sát trượt của đường. Tính tốc độ tối đa cho phép v (m/s) để lái xe an toàn khi đi qua đoạn đường có dạng cung tròn với bán kính r=400 m (làm tròn kết quả đến hàng phần mười).
Trả lời:
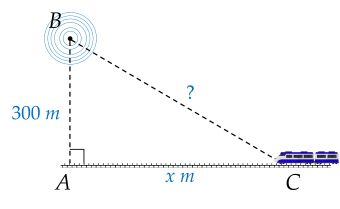
Một trạm phát sóng được đặt ở vị trí B cách đường tàu một khoảng AB=300 m. Đầu tàu đang ở vị trí C, cách vị trí A một khoảng AC=x m.
Biểu thức biểu thị khoảng cách từ trạm phát sóng đến đầu tàu là
Tính khoảng cách trên khi x=1000 (kết quả làm tròn đến hàng đơn vị của mét).
Trả lời:
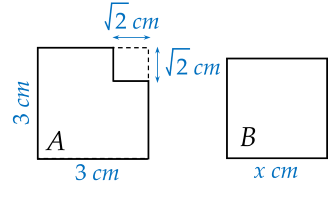
Biết rằng hình A và hình vuông B trong hình trên có diện tích bằng nhau. Độ dài cạnh x của hình vuông B là
