Bài học cùng chủ đề
Báo cáo học liệu
Mua học liệu
Mua học liệu:
-
Số dư ví của bạn: 0 coin - 0 Xu
-
Nếu mua học liệu này bạn sẽ bị trừ: 2 coin\Xu
Để nhận Coin\Xu, bạn có thể:

Phần tự luận (8 điểm) SVIP
Bài 1. (1 điểm) Với giá trị nào của $m$ thì các hàm số sau là hàm số bậc nhất?
a) $y=\left(m^2+1\right) x+m$.
b) $y=m-(3-2 m) x$.
Hướng dẫn giải:
a) Để $y=\left(m^2+1\right) x+m$ là hàm số bậc nhất $\Rightarrow m^2+1 \neq 0$.
Mà $m^2 \geq 0$ với mọi $m \Rightarrow m^2+1 \geq 1>0$ với mọi $m$.
Vậy $y=\left(m^2+1\right) x+m$ là hàm số bậc nhất với mọi $m$.
b) Để $y=m-(3-2 m) x$ là hàm số bậc nhất $3-2 m \neq 0 \Rightarrow 2 m \neq 3 \Rightarrow m \neq \dfrac{3}{2}$.
Vậy $m \neq \dfrac{3}{2}$ thì $y=m-(3-2 m) x$ là hàm số bậc nhất.
Bài 2. (1 điểm) Cho hai hàm số: $d_1: \, y=\dfrac{1}{4} x+3$ và $d_2: \, y=5 x+4$.
a) Vẽ đồ thị của các hàm số trong cùng một mặt phẳng tọa độ.
b) Tìm tọa độ giao điểm của $d_1$ với hai trục tọa độ.
Hướng dẫn giải:
a)
+ Xét hàm số $y=\dfrac{1}{4} x+3$.
Thay $x=0 \Rightarrow y=3$.
Đồ thị hàm số $y=\dfrac{1}{4} x+3$ đi qua điểm có tọa độ $(0 ; 3)$.
Thay $x=4 \Rightarrow y=4$.
Đồ thị hàm số $y=\dfrac{1}{4} x+3$ đi qua điểm có tọa độ $(4 ; 4)$.
+ Xét hàm số $d_2: \, y=5 x+4$.
Thay $x=0 \Rightarrow y=4$.
Đồ thị hàm số $d_2: \, y=5 x+4$ đi qua điểm có tọa độ $(0 ; 4)$.
Thay $x=-1 \Rightarrow y=-1$.
Đồ thị hàm số $d_2: \, y=5 x+4$ đi qua điểm có tọa độ $(-1 ;-1)$.
+ Ta vẽ hai đồ thị:
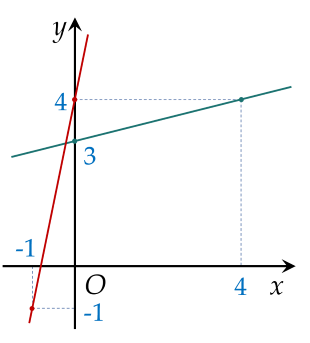
b) Để tìm giao điểm của $d_1: \, y=\dfrac{1}{4} x+3$ với trục hoành, ta xét $y=0 \Rightarrow \dfrac{1}{4} x+3=0 \Rightarrow x=-12$.
Vậy $d_1: \, y=x+5$ giao với trục hoành tại điểm có tọa độ $(-12 ; 0)$.
Để tìm giao điểm của $d_1: \, y=\dfrac{1}{4} x+3$ với trục tung, ta xét $x=0 \Rightarrow y=\dfrac{1}{4} . 0+3=3$.
Vậy $d_1: \, y=x+5$ giao với trục tung tại điểm có tọa độ $(0 ; 3)$.
Bài 3. (1,5 điểm) Cho đường thẳng $y=a x+b$. Tìm $a, \, b$ biết rằng:
a) Đường thẳng $y=a x+b$ đi qua $F(1 ; 2)$ và song song với đường thẳng $y=3 x-7$.
b) Đường thẳng $y=a x+b$ đi qua điểm $A(-2 ; 5)$ và đi qua giao điểm của hai đường thẩng $\left(d_1\right): \, y=2 x-7 ; \, \left(d_2\right): \, y=-3 x+3$.
Hướng dẫn giải:
a) Vi đường thẳng $y=a x+b$ song song với đường thẳng $y=3 x-7$ nên $a=3$ và $b \neq-7$.
Khi đó đường thẳng cần tìm có dạng $y=3 x+b$ với $b \neq-7$.
Vì $y=3 x+b$ đi qua điểm $F(1 ; 2)$ nên $2=3.1+b \Rightarrow 2=3+b \Rightarrow b=-1$ (thỏa mãn).
Vậy đường thẳng cần tìm là $y=3 x-1$.
b) Vì đường thẳng $y=ax+b$ đi qua điểm $A(-2 ; 5)$ nên: $5=-2 . a+b$ hay $b=5+2 a$ $(*)$
Gọi tọa độ giao điểm của $\left(d_1\right): \, y=2 x-7$ và $\left(d_2\right): \, y=-3 x+3$ là $B\left(x_0 ; y_0\right)$
$\left(d_1\right): \, y=2 x-7$ đi qua $B\left(x_0 ; y_0\right)$ nên: $y_0=2 x_0-7$ (1)
$\left(d_2\right): \, y=-3 x+3$ đi qua $B\left(x_0 ; y_0\right)$ nên $y_0=-3 x_0+3$ (2)
Từ (1) và (2) ta có $2 x_0-7=-3 x_0+3 \Rightarrow x_0=2 \Rightarrow y_0=-3.2+3=-3 \Rightarrow B(2 ;-3)$.
Vì đường thẳng $y=a x+b$ đi qua điểm $B(2 ;-3)$ nên: $-3=2 a+b$ hay $2 a+b=-3$ $(* *)$
Thay $\left(*\right)$ vào $\left(* *\right)$ ta được: $2 a+5+2 a=-3 \Rightarrow 4 a=-8 \Rightarrow a=-2 \Rightarrow b=5+2 .(-2)=1$.
Vậy đường thẳng cần tìm là $y=-2 x+1$.
Bài 4. (1 điểm) Quãng đường giữa hai thành phố $A$ và $B$ là $120$ km. Lúc 6 giờ sáng, một ô tô xuất phát từ $A$ đi về $B$. Người ta nhận thấy mối liên hệ giữa khoảng cách của ô tô so với thành phố $A$ và thời điểm đi của ô tô là một hàm số bậc nhất $y=a x+b$ có đồ thị như hình vẽ.
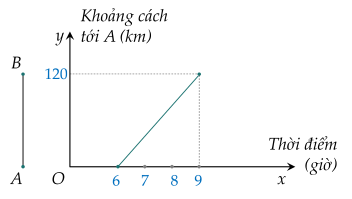
a) Xác định các hệ số $a ; \, b$.
b) Hỏi lúc 8 giờ sáng, ô tô còn cách $B$ bao nhiêu km?
Hướng dẫn giải:
a) Dựa vào hình vẽ ta thấy nếu $x<6$ thì $y=0$.
Hàm số $y=a x+b$ đi qua điểm $(6 ; 0)$ nên: $0=a .6+b \Rightarrow b=-6 a$.
Hàm số $y=a x+b$ đi qua điểm $(9 ; 120)$ nên: $120=a .9+b \Rightarrow 120=9 a-6 a \Rightarrow a=40 \Rightarrow b=-6.40=-240$.
Vậy $a=40$; $b=-240$.
Hàm số bậc nhất có dạng $y=40 x-240$.
b) Quãng đường ô tô đó đi được từ 6 giờ sáng đến 8 giờ sáng là: $y=8.40-240=80$ km.
Khi đó, ô tô còn cách $B$ số ki-lô-mét là:
$120-80=40$ (km).
Bài 5. (3,5 điểm)
1. Cho tam giác $P M N$. Đường thẳng song song với $M N$ cắt $P M$ và $P N$ lần lượt tại $A$ và $B$. Biết $A M=4$ cm; $A P=3$ cm; $M N-A B=8$ cm. Tính độ dài các đoạn thẳng $M N$ và $A B$.
2. Cho hình bình hành $ABCD$. Đường phân giác của góc $A$ cắt $BD$ tại $E$. Đường phân giác của góc $B$ cắt $A C$ tại $F$. Gọi $O$ là giao điểm giữa $AC$ và $BD$. Chứng minh rằng:
a) $\dfrac{B E}{E D}=\dfrac{F A}{F C}$.
b) Chứng minh $\dfrac{O D}{E D}=\dfrac{O C}{F C}$, từ đó suy ra $E F$ // $C D$.
Hướng dẫn giải:
1.
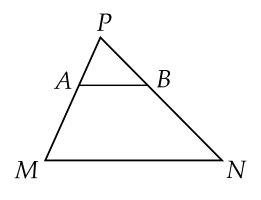
Xét $\Delta P M N$ có $A B$ // $M N$ (gt)
Suy ra $\dfrac{A B}{M N}=\dfrac{A P}{P M}$ (hệ quả định lí Thalès).
Thay số: $\dfrac{A B}{M N}=\dfrac{A P}{A P+A M}=\dfrac{3}{3+4}=\dfrac{3}{7} \Rightarrow \dfrac{M N}{7}=\dfrac{A B}{3}$.
Áp dụng tính chất dãy tỉ số bằng nhau: $\dfrac{M N}{7}=\dfrac{A B}{3}=\dfrac{M N-A B}{7-3}=\dfrac{8}{4}=2$
Suy ra $M N=2.7=14$ cm; $A B=2.3=6$ cm.
Vậy $M N=14$ cm; $A B=6$ cm.
2
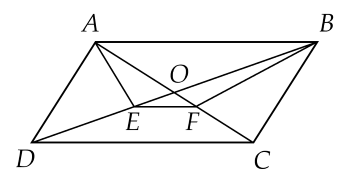
a) Xét $\Delta A D B$ có $A E$ là phân giác trong của đỉnh $A$ (gt) suy ra $\dfrac{B E}{E D}=\dfrac{A B}{A D}$ (tính chất đường phân giác của tam giác).
Xét $\Delta B A C$ có $B F$ là phân giác trong của đỉnh $B$ (gt) suy ra $\dfrac{F A}{F C}=\dfrac{A B}{B C}$ (tính chất đường phân giác của tam giác)
Thêm nữa $A D=B C$ (do $A B C D$ là hình bình hành) suy ra $\dfrac{B E}{E D}=\dfrac{F A}{F C}$.
Vậy ta có điều phải chứng minh.
b) Từ câu a ta có: $\dfrac{B E}{E D}=\dfrac{F A}{F C}$ suy ra $\dfrac{B E+E D}{E D}=\dfrac{F A+F C}{F C}$
$\Rightarrow \dfrac{D B}{E D}=\dfrac{A C}{F C} \Rightarrow \dfrac{2 O D}{E D}=\dfrac{2 O C}{F C} \Rightarrow \dfrac{O D}{E D}=\dfrac{O C}{F C}$
Xét $\Delta O D C$ có: $\dfrac{O D}{E D}=\dfrac{O C}{F C}$ (cmt) suy ra $E F$ // $C D$ (định lí Thalès đảo)
Vậy ta có điều phải chứng minh.
