Phần tự luận (7 điểm) SVIP

Hướng dẫn giải:

a) $2\sqrt{x^2-2x+1}-4=0$

$2\sqrt{(x-1)^2}=4$

$|x-1|=2$

$x-1=2$ hoặc $x-1=-2$

$x=3$ hoặc $x=-1$.

Vậy phương trình có nghiệm $x=3$ hoặc $x=-1$.

b) $5x-4-3(2x-9) \ge 5x-8$

$5x-4-6x+27 \ge 5x-8$

$5x-6x-5x \ge -8-27+4$

$-6x \ge -31$

$x \le \dfrac{31}{6}$.

Vậy nghiệm của bất phương trình là $x \le \dfrac{31}{6}$.

Hướng dẫn giải:

a)

$A=\Big(\dfrac{3\sqrt{x}}{\sqrt{x}-1}-\dfrac{1}{\sqrt{x}+1}-3 \Big) .\dfrac{\sqrt{x}+1}{\sqrt{x}+2}$ (với $x\ge 0;\,x\ne 1$)

$ A=\dfrac{3\sqrt{x}(\sqrt{x}+1)-1(\sqrt{x}-1)-3(x-1)}{x-1}.\dfrac{\sqrt{x}+1}{\sqrt{x}+2} $

$ A=\dfrac{3x+3\sqrt{x}-\sqrt{x}+1-3x+3}{x-1}.\dfrac{\sqrt{x}+1}{\sqrt{x}+2} $

$ A=\dfrac{2\sqrt{x}+4}{(\sqrt{x}+1)(\sqrt{x}-1)}.\dfrac{\sqrt{x}+1}{\sqrt{x}+2} $

$ A=\dfrac{2}{\sqrt{x}-1} $

Vậy $A=\dfrac{2}{\sqrt{x}-1}$ với $x\ge 0;x\ne 1$

b) Với $x\ge 0;x\ne 1$

Để $A$ nguyên thì $\sqrt{x}-1$ thuộc ước của $2$.

Ta tìm được $x = 0$ hoặc $x = 4$ (TMĐK).

Vậy để $A$ nguyên thì $x = 0$ hoặc $x = 4$.

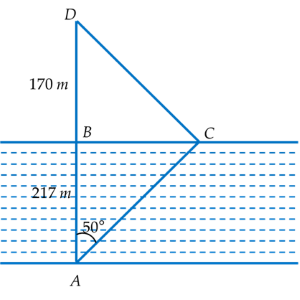
Hướng dẫn giải:

$AC=\dfrac{21}{\cos \widehat{BAC}} = \dfrac{217}{\cos 50^\circ} \approx 337,592 $ m

$BC = AB . \tan\widehat{BAC} = 217. 50^\circ = 258,611 $ m.

$CD = \sqrt{BD^2 + BC^2} = \sqrt{170^2 + 258,611^2} = 309,482$ m.

Quãng đường Hùng đi từ $A$ đến $D$ là

$AC + CD = 337,592 + 309,482 = 647,075$ m.

Hướng dẫn giải:

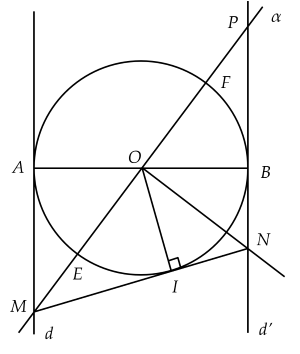
a) Xét $\Delta AOM$ và $\Delta BOP$ có:

$OA=OB=R$ (giả thiết)

$\widehat{OAM}=\widehat{OBM}=90^\circ$ (giả thiết)

$\widehat{MOA} = \widehat{BOP}$ (đối đỉnh)

Do đó $\Delta AOM = \Delta BOP$ (cạnh góc vuông - góc nhọn kề).

Suy ra $OM = OP$ (hai cạnh tương ứng).

b) Theo giả thiết, có $ON$ vuông góc với $MP$.

Mà $OM = OP$ nên suy ra tam giác $MNP$ cân tại $N$.

Suy ra $N$ nằm trên tiếp tuyến của đường tròn $(O)$.

Lại có $OI \bot MN$ nên $MN$ là tiếp tuyến của $(O)$ tại $I$.

$\widehat{AMP} = \widehat{PMB}$ ($\Delta AOM = \Delta BOP$) (1)

Xét $\Delta MNP$ có $NO$ là đường cao đồng thời là đường trung tuyến nên $\Delta MNP$ cân tại $N$

Suy ra $\widehat{NMP} = \widehat{NPM}$ (2)

Từ (1) và (2) suy ra $\widehat{AMP} = \widehat{NMP}$

Suy ra  $\Delta AMO = \Delta IMO$ (cạnh huyền - góc nhọn)

Suy ra $ \widehat{AOM} = \widehat{IOM}$ (hai góc tương ứng)

Có $\widehat{IOM} = \widehat{NOM} -\widehat{ION} = 90^\circ -\widehat{ION}$

Lại có $\widehat{BNO} = 90^\circ -\widehat{BON}$

Mà $\widehat{ION}=\widehat{BON}$ (Vì $MN, PN$ là hai tiếp tuyến cắt nhau)

$\widehat{IOM} = \widehat{BNO}$

Suy ra $\widehat{IOM} = \widehat{BNO}$

Mà $\widehat{OAM} = \widehat{NBO}= 90^\circ$

$\Delta OAM \sim \Delta NBO$ (g-g)

Suy ra $\dfrac{AM}{AO} = \dfrac{OB}{BN}$

Hay $MA. NB = OA. OB = R^2$.

c) Xét tam giác $MOI$, có: $\cos \widehat{IOM} = \dfrac{OI}{OM} = \dfrac{R}{2R} = \dfrac{1}{2}$.

Suy ra $\widehat{IOM}=60^\circ$.

Do $ON$ vuông góc với $MP$ nên $\widehat{NOM} = 90^\circ$.

Ta có: $\widehat{NOM} = \widehat{NOI} +\widehat{IOM}$ nên $\widehat{NOI} = \widehat{NOM} - \widehat{IOM} =90^\circ-60^\circ=30^\circ$.

Suy ra $\widehat{IOF} =\widehat{ ION} + \widehat{NOF} = 30^\circ+90^\circ =120^\circ$.

Do đó, $S=\dfrac{n\pi R^2}{360} = \dfrac{120.\pi R^2}{360}=\dfrac{\pi R^2}{3}$.

Vậy diện tích hình quạt giới hạn bởi $OI, OF$ và cung nhỏ $IF$ là $\dfrac{\pi R^2}{3}$.

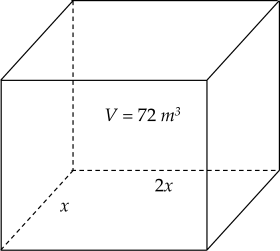
Hướng dẫn giải:

Chiều dài của đáy bể là $2x$ (m).

Diện tích đáy của bể là $2x^2$ (m$^2$).

Chiều cao của bể là: $\dfrac{72}{2x^2} = \dfrac{36}{x^2}$ (m)

Diện tích xung quanh của bể là: $2. \dfrac{36}{x^2}. (x+2x)=\dfrac{72.3x}{x^2} = \dfrac{216}{x}$ (m$^2$)

Diện tích cần sơn bằng tổng diện tích xung quanh và diện tích đáy của bể, và bằng: $\dfrac{216}{x} + 2x^2$ (m$^2$)

Do $x$ là chiều rộng của bể nên $x> 0$, áp dụng bất đẳng thức Cauchy, ta có:

$2x^2 + \dfrac{216}{x}= 2x^2 + \dfrac{108}{x} + \dfrac{108}{x} \ge 3 \sqrt[3]{2x^2 . \dfrac{108}{x} . \dfrac{108}{x}}$

Suy  ra $2x^2 + \dfrac{216}{x} \ge \sqrt[3]{23\, 328} \approx 85,72$.

Dấu “$=$" xảy ra khi $2.x^2 = \dfrac{108}{x} = \dfrac{108}{x} $ hay $2x^3 = 108$, tức là $x=\sqrt[3]{54} \approx 3,78$

Vậy muốn diện tích cần xây là tiết kiệm chi phí nhất thì $x \approx 3,78$ m.