Bài học cùng chủ đề
Báo cáo học liệu
Mua học liệu
Mua học liệu:
-
Số dư ví của bạn: 0 coin - 0 Xu
-
Nếu mua học liệu này bạn sẽ bị trừ: 2 coin\Xu
Để nhận Coin\Xu, bạn có thể:

Phần tự luận (7 điểm) SVIP
Câu 13. (1,0 điểm). Viết bất đẳng thức để mô tả tình huống sau:
a) Bạn An ít nhất $18$ tuổi mới được đi bầu cử đại biểu Quốc hội.
b) Một thang máy chở được tối đa $700$ kg.
c) Bạn phải mua hàng có tổng trị giá ít nhất $1$ triệu đồng mới được giảm giá.
d) Giá trị của biểu thức $2x-3$ lớn hơn giá trị biểu thức $-7x+2$.
Hướng dẫn giải:
a) Gọi số tuổi của bạn An là $x$ (tuổi), $x \in \mathbb{N}^*$.
Bất đẳng thức để mô tả bạn An ít nhất $18$ tuổi mới được đi bầu cử đại biểu Quốc hội là: $x\ge 18$.
b) Gọi khối lượng thang máy chở được là $a$ kg, $a>0$.
Bất đẳng thức để mô tả một thang máy chở được tối đa $700$ kg là: $0<a \le 700$.
c) Gọi số tiền mua hàng là $x$ (triệu đồng), $x>0$.
Bất đẳng thức để mô tả bạn phải mua hàng có tổng trị giá ít nhất $1$ triệu đồng mới được giảm giá là $x \ge 1$.
d) $2x-3>-7x+2$.
Câu 14. (2,0 điểm). Giải các phương trình và hệ phương trình sau:
a) $\left( 3x-2 \right)\left( 2x+1 \right)=0$
b) $\left\{ \begin{aligned} & 2x-y=4 \\ & x+2y=-3 \\ \end{aligned} \right.$
Hướng dẫn giải:
a) Để giải phương trình đã cho ta giải hai phương trình sau:
(1) $3x-2=0$
$3x=2$
$x=\dfrac{2}{3}$
(2) $2x+1=0$
$2x=-1$
$x=\dfrac{-1}{2} $.
Vậy phương trình đã cho có hai nghiệm là $x=\dfrac{2}{3}$ và $x=\dfrac{-1}{2}$.
b) $ \left\{ \begin{aligned} & 2x-y=4 \\ & x+2y=-3 \\ \end{aligned} \right. $
$\left\{ \begin{aligned} & 4x-2y=8 \\ & x+2y=-3 \\ \end{aligned} \right. $
$\left\{ \begin{aligned} & 5x=5 \\ & x+2y=-3 \\ \end{aligned} \right. $
$\left\{ \begin{aligned} & x=1 \\ & 1+2y=-3 \\ \end{aligned} \right.$
$\left\{ \begin{aligned} & x=1 \\ & 2y=-4 \\ \end{aligned} \right. $
$\left\{ \begin{aligned} & x=1 \\ & y=-2 \\ \end{aligned} \right.$.
Vậy hệ đã cho có nghiệm duy nhất $\left( x;y \right)=\left( 1;-2 \right)$
Câu 15. (1,0 điểm). Bác Phương chia số tiền $800$ triệu đồng của mình cho hai khoản đầu tư. Sau một năm, tổng số tiền lãi bác thu được là $54$ triệu đồng. Lãi suất cho khoản đầu tư thứ nhất là $6\%$/năm và khoản đầu tư thứ hai là $8\%$/năm. Tính số tiền bác Phương đầu tư cho mỗi khoản.
Hướng dẫn giải:
Gọi $x$, $y$ (triệu đồng) lần lượt là số tiền hai khoản đầu tư của bác Phương ($x, \, y>0$)
Tổng số tiền bác Phương đầu tư là $800$ triệu đồng nên ta có phương trình $x+y=800$ (1)
Lãi suất cho khoản đầu tư thứ nhất là $6\%$/năm và khoản đầu tư thứ hai là $8\%$/năm, nên ta có phương trình
$0,06.x+0,08.y=54$ (2)
Từ (1) và (2) ta có hệ phương trình $\left\{ \begin{aligned} & x+y=800 \\ & 0,06.x+0,08.y=54 \\ \end{aligned} \right.$
Giải hệ phương trình ta được $\left\{ \begin{aligned} & x=500 \\ & y=300 \\ \end{aligned} \right.$ (thỏa mãn)
Vậy bác Phương đầu tư cho khoản thứ nhất và khoản thứ hai lần lượt là $500$ triệu đồng và $300$ triệu đồng.
Câu 16. (2,0 điểm). Cho $\Delta ABC$ có $\widehat{A}= 90^\circ$. Từ trung điểm $E$ của cạnh $AC$ kẻ $EF \perp BC$. Nối $AF$ và $BE$.
a) Chứng minh $AF = BE.\cos C$.
b) Biết $BC = 10$ cm, $\sin C = 0,6$. Tính diện tích tứ giác $ABFE$.
Hướng dẫn giải:

a) $\Delta CEF \backsim \Delta CBA$ (g-g) suy ra $\dfrac{CF}{CE}=\dfrac{AC}{BC}$ nên
$\Delta CFA \backsim \Delta CEB$ (c-g-c) suy ra $\dfrac{AF}{BE}=\dfrac{AC}{BC}$ hay $\dfrac{AF}{BE}=\cos C$.
Vậy $AF = BE.\cos C$.
b) Vì $\Delta ABC$ có $\widehat{A}=90^\circ$ nên $AB = \sin C. BC = 0,6.10 = 6$ cm.
Suy ra $AC=8$ cm nên $AE = EC = 4$ cm.
Mà $EF = \sin C. EC = 0,6. 4 = 2,4$ cm.
Suy ra $FC=3,2$ cm (Định lí Pythagore)
$S_{ABFE} = S_{ABC} - S_{CFE} = \dfrac{1}{2}. \left( AB. AC-EF. FC \right)=\dfrac{1}{2}\left( 6\cdot 8-2,4\cdot 3,2 \right)= 20,16$ (cm$^2$).
Câu 17. (1,0 điểm). Người ta làm một con đường gồm ba đoạn thẳng $AB, \, BC, \, CD$ bao quanh hồ nước (Hình vẽ).
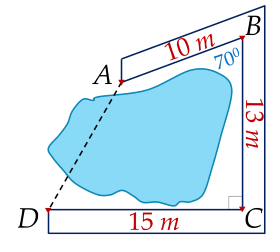
Tính khoảng cách $AD$. (làm tròn kết quả đến chữ số thập phân thứ hai).
Hướng dẫn giải:
Vẽ $AK \bot BC$ tại K, $AH \bot DC$ tại $H$.
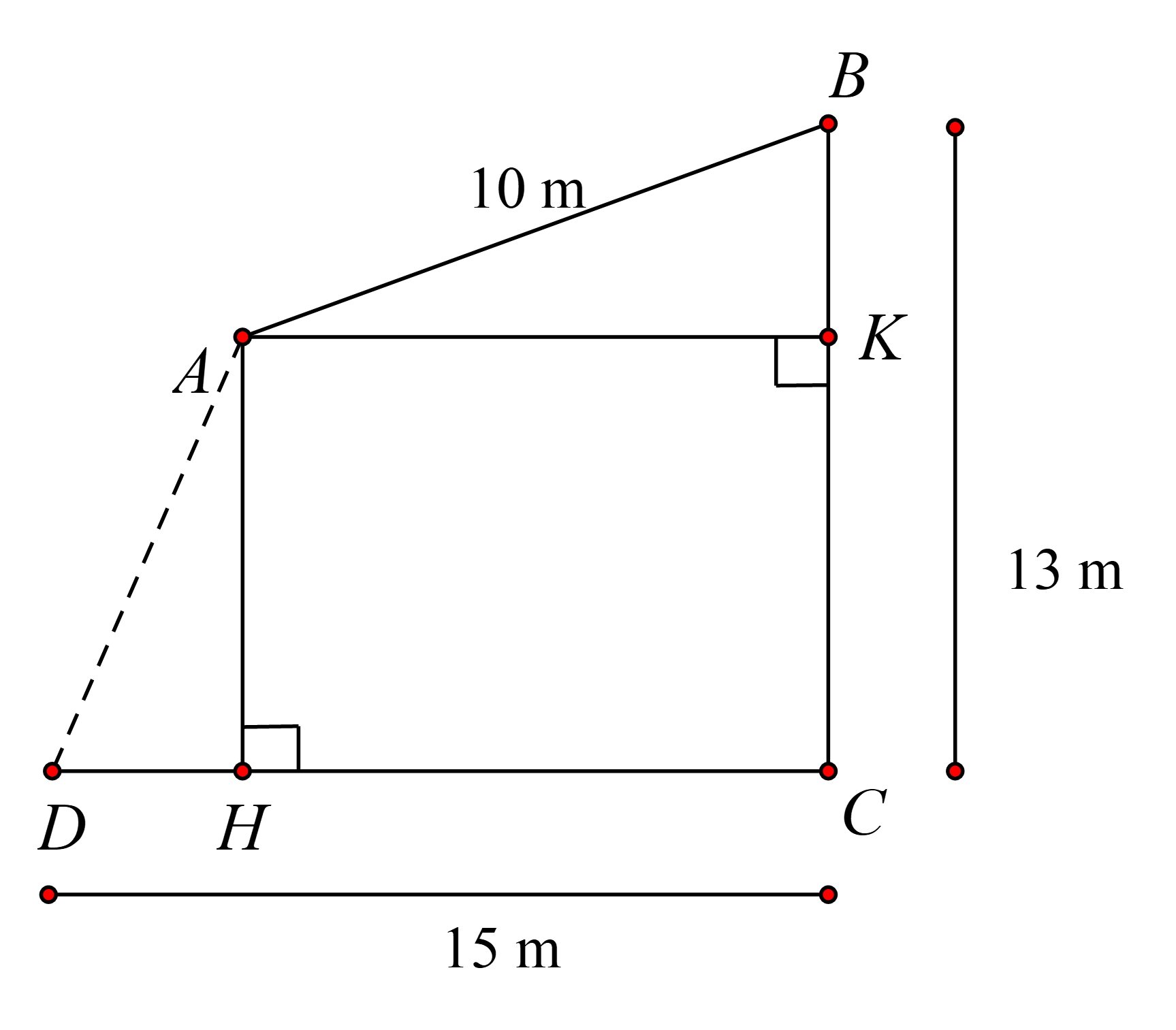
Khi đó tứ giác $AKCH$ là hình chữ nhật nên $AK=CH$; $AH=CK$
Trong tam giác vuông $AKB$ vuông tại $K$ có $AB=10$ cm, $\widehat{ABK}=70^\circ$
$AK=AB. \sin 70^\circ=10. \sin 70^\circ$ suy ra $AK=CH=10. \sin 70^\circ$
hay $DH=CD-HC=15-10. \sin 70^\circ$
$BK=AB. \cos 70^\circ=10. \cos 70^\circ$
Suy ra $CK=CB-BK=13-10. \cos 70^\circ$
hay $AH=CK=13-10. \cos 70^\circ$
Theo định lí Pythagore trong tam giác vuông $ADH$:
$AD=\sqrt{AH^2+DH^2}=\sqrt{(13-10.\cos70^\circ)^2+(15-10. \sin70^\circ )^2} \approx 11,1$ m.
