Bài học cùng chủ đề
Báo cáo học liệu
Mua học liệu
Mua học liệu:
-
Số dư ví của bạn: 0 coin - 0 Xu
-
Nếu mua học liệu này bạn sẽ bị trừ: 2 coin\Xu
Để nhận Coin\Xu, bạn có thể:

Phần tự luận (7 điểm) SVIP
1. Một hộp có $10$ chiếc thẻ cùng loại, mỗi thẻ ghi một trong các số $0, 1, 2, 3, …, 9$. Rút ngẫu nhiên một chiếc thẻ trong hộp.
a) Viết tập hợp $A $ gồm các kết quả có thể xảy ra đối với số xuất hiện trên thẻ được rút ra.
b) Liệt kê các kết quả có lợi cho biến cố $B$: “Số xuất hiện trên thẻ được rút là số nguyên tố.”
Tính xác suất của biến cố $B$.
2. Cửa hàng X thống kê lại số lượt khách đến cửa hàng tại các thời điểm trong ngày bằng biểu đồ bên dưới.
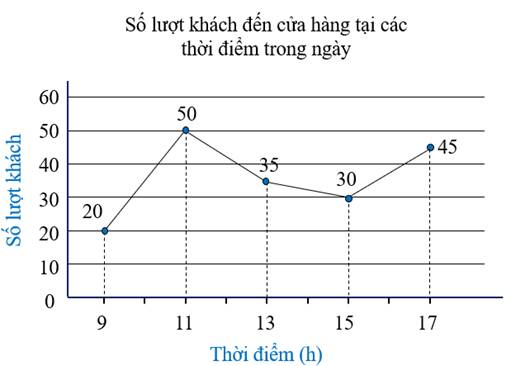
a) Cửa hàng đông khách nhất vào thời điểm nào? Vắng khách nhất vào thời điểm nào?
b) Số lượt khách đến cửa hàng từ $15$ giờ đến $17$ giờ tăng hay giảm bao nhiêu lượt khách?
Hướng dẫn giải:
1. a) $A=\{0 ; 1 ; 2 ; 3 ; 4 ; 5 ; 6 ; 7 ; 8 ; 9\}$
b) $B=\{2 ; 3 ; 5 ; 7\}$
Ta thấy tập ${A}$ có $10$ phần tử, tập ${B}$ có $4$ phần tử.
Xác suất của biến biến cố ${B}$ là:
$\dfrac{4}{10}=\dfrac{2}{5}$
2. a) Cửa hàng đông khách nhất vào thời điểm $11$ giờ, vắng khách nhất vào thời điểm $9$ giờ.
b) Từ $15$ giờ đến $17$ giờ, số lượt khách đến cửa hàng tăng:
$45-30=15$ (lượt khách)
Cho các đa thức:
$A(x)=x^3-2 x^2+5 x-3$
${B}(x)=-x^3+2 x^2-3 x+5$
$C(x)=x-3$
a) Tính $P(x)=A(x)+B(x)$.
b) Tính $Q(x)=A(x) \cdot {C}(x)$.
c) Tìm nghiệm của đa thức $P(x)$.
Hướng dẫn giải:
a) Tính $P(x)=A(x) + B(x)$
$A(x)+{B}(x)=\left(x^3-2 x^2+5 x-3\right)+\left(-x^3+2 x^2-3 x+5\right)$
$=x^3-2 x^2+5 x-3-x^3+2 x^2-3 x+5$
$=\left(x^3-x^3\right)+\left(-2 x^2+2 x^2\right)+(5 x-3 x)+(-3+5) $
$=2 x+2$
b) $Q(x)=A(x) . {C}(x)=\left(x^3-2 x^2+5 x-3\right)(x-3)$
$=\left(x^3-2 x^2+5 x-3\right) .(x-3)$
$=x^3 . x-2 x^2 . x+5 x . x-3 . x-3 x^3-3 .\left(-2 x^2\right)-3 . 5 x+(-3) .(-3)$
$=x^4-2 x^3+5 x^2-3 x-3 x^3+6 x^2-15 x+9 $
$=x^4+\left(-2 x^3-3 x^3\right)+\left(5 x^2+6 x^2\right)+(-3 x-15 x)+9$
$=x^4-5 x^3+11 x^2-18 x+9$
c) Để tìm nghiệm của đa thức $P(x)$. Ta cần tìm giá trị của $x$ để $2 x+2=0$.
$2 x+2=0$
$2 x=-2$
$x=-1$
Cho tam giác $A B C$ vuông tại $B$, phân giác $A D$. Kẻ $D E \perp A C(E \in A C)$.
Chứng minh:
a) $\Delta B A D=\Delta E A D$.
b) $A D$ là trung trực của $B E$.
c) Trên tia đối của tia $B A$ lấy điểm $K$ sao cho $B K=C E$. Chứng minh ba điểm $E, D, K$ thẳng hàng.
Hướng dẫn giải:
a) Xét $\Delta B A D$ và $\Delta E A D$:
$\widehat{{ABD}}=\widehat{{AED}}=90^{\circ} $.
$AD$ chung.
$\widehat{{BAD}}=\widehat{{EAD}}({gt})$.
Suy ra $\Delta {BAD}=\Delta {EAD}$ (cạnh huyền - góc nhọn)
b) Do $\Delta B A D=\Delta E A D$ (câu a) nên
+ ) $A B=A E$ (Cặp cạnh tương ứng)
$A$ nằm trên đường trung trực của đoạn thẳng $B E$ (1)
+) $D B=D E$ (Cặp cạnh tương ứng)
$D$ nằm trên đường trung trực của đoạn thẳng $B E$ (2)
Từ (1) và (2) ta suy ra $A D$ là đường trung trực của $B E$.
c) Xét $\Delta BDK$ và $\Delta EDC$:
$BK=CE$ (gt).
$\widehat{{KBD}}=\widehat{{CED}} = 90^\circ$.
$BD=DE$ (chứng minh trên).
Suy ra $\Delta BDK=\Delta EDC$ (c.g.c)
Suy ra $\widehat{B D K}=\widehat{E D C}$ (Cặp góc tương ứng) (3)
Mặt khác ta có $D$ thuộc cạnh $B C$ nên $\widehat{E D C}+\widehat{E D B}=180^{\circ}$. (4)
Từ (3) và (4) suy ra $\widehat{B D K}+\widehat{E D B}=180^{\circ}$.
Hay ba điểm $E, D, K$ thẳng hàng.
Cho $M(x)=x^8-101 x^7+101 x^6-101 x^5+...+101 x^2-101 x+125$.
Tính $M(100)$.
Hướng dẫn giải:
$M(x)=x^8-101 x^7+101 x^6-101 x^5+...+101 x^2-101 x+125$
$ =x^8-100 x^7-x^7+100 x^6+x^6-100 x^5-x^5+...+100 x^2+x^2-100 x-x+100+25$
$=x^7(x-100)-x^6(x-100)+x^5(x-100)-...+x(x-100)-(x-100)+25$
Vậy $M(100)=25$.
