Phần tự luận (7 điểm) SVIP

Hướng dẫn giải:

+ Thay giá trị $x=4$ vào công thức hàm số $y=f\left(x \right)=3\sqrt{x}+5$ ta được:

$f\left(4 \right)=3\sqrt{4}+5=3\sqrt{2^2}+5=3\left| 2 \right|+5=3.2+5=11$ (Vì $2>0$)

Vậy $f\left(4 \right)=11$.

+ Thay giá trị $x=\dfrac{1}{9}$ vào công thức hàm số $y=f\left(x \right)=3\sqrt{x}+5$ ta được:

$f\left(\dfrac{1}{9} \right)=3\sqrt{\dfrac{1}{9}}+5=3\sqrt{{{\left(\dfrac{1}{3} \right)}^2}}+5=3. \left| \dfrac{1}{3} \right|+5=3-\dfrac{1}{3}+5=6$

Vậy $f\left(\dfrac{1}{9} \right)=6$.

Hướng dẫn giải:

a) Đồ thị hàm số $y=ax+2$ đi qua điểm $M\left(1;3 \right)$ nên: $3=a.1+2\Leftrightarrow a=1$.

Vậy đường thẳng có hệ số góc là: $a=1$.

b) Đồ thị cần tìm là: $y=x+2$.

Cho $x=0$ thì $y=2$.  Đồ thị đi qua điểm $B\left(0;2 \right)$;

Cho $y=0$ thì $x+2=0$ hay $x=-2$. Đồ thị đi qua điểm $A\left(0;2 \right)$.

Từ đây ta có đồ thị hàm số:

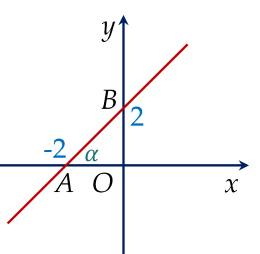
c) Tam giác $OAB$ có $OA=OB=2$ (cm) nên: $\Delta OAB$ cân tại $O$.

Mặt khác: $\widehat{AOB}={{90}^{\circ}}$.

Do đó $\widehat{OAB}=\widehat{OBA}=\dfrac{{{90}^\circ}}{2}={{45}^\circ}$.

Hướng dẫn giải:

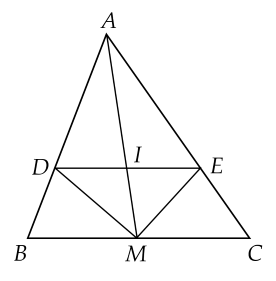
a) Theo tính chất đường phân giác ta có $\dfrac{DA}{DB}=\dfrac{MA}{MB}$ và $\dfrac{EA}{EC}=\dfrac{MA}{MC}$.

Mặt khác $MB=MC$ nên $\dfrac{DA}{DB}=\dfrac{EA}{EC}$.

Theo định lí Thalès đảo ta được $DE$ // $BC$.

b) Theo câu a ta có $DE$ // $BC$ nên $\dfrac{AD}{AB}=\dfrac{AE}{AC}$.

Xét định lí Thalès cho $\Delta ABM$ và $\Delta ACM$ ta có $\dfrac{AD}{AB}=\dfrac{DI}{BM}$ và $\dfrac{AE}{AC}=\dfrac{IE}{CM}$.

Từ đó suy ra $\dfrac{DI}{BM}=\dfrac{IE}{CM}$ mà $MB=CM$ nên $DI=IE$ hay $I$ là trung điểm của $DE$.

Hướng dẫn giải:

Ta có: $E\left(x \right)=2\left({{x}^{2}}+4xy+4{{y}^{2}} \right)+3{{y}^{2}}-4x-2y+6$

$=\left[ 2{{\left(x+2y \right)}^{2}}-4\left(x+2y \right)+2 \right]+3{{y}^{2}}+6y+4$

$=2{{\left(x+2y-1 \right)}^{2}}+3{{\left(y+1 \right)}^{2}}+1\ge 1$.

Vậy giá trị nhỏ nhất của $E$ là: $1$ tại $\left\{ \begin{aligned} & x+2y-1=0 \\ & y+1=0 \\ \end{aligned} \right.$ hay $\left\{ \begin{aligned} & x=3 \\ & y=-1 \\ \end{aligned} \right.$