Bài học cùng chủ đề
Báo cáo học liệu
Mua học liệu
Mua học liệu:
-
Số dư ví của bạn: 0 coin - 0 Xu
-
Nếu mua học liệu này bạn sẽ bị trừ: 2 coin\Xu
Để nhận Coin\Xu, bạn có thể:

Phần tự luận (7 điểm) SVIP
Bài 1. (2 điểm) Phân tích các đa thức sau thành nhân tử:
a) ${{x}^{2}}+2xy+{{y}^{2}}-x-y$.
b) $2{{x}^{3}}+6{{x}^{2}}+12x+8$.
Hướng dẫn giải:
a) ${{x}^{2}}+2xy+{{y}^{2}}-x-y = \left( x+y \right)\left( x+y-1 \right)$;
b) $2{{x}^{3}}+6{{x}^{2}}+12x+8 = \left( 2x+2 \right)\left( {{x}^{2}}+2x+4 \right)$.
Bài 2 (2 điểm). Tìm $x$, biết rằng:
a) $x-3={{\left( 3-x \right)}^{2}}$
b) ${{x}^{3}}+\dfrac{3}{2}{{x}^{2}}+\dfrac{3}{4}x+\dfrac{1}{8}=\dfrac{1}{64}$
Hướng dẫn giải:
a) Ta có: $x-3={{\left( 3-x \right)}^{2}}$
$\left( x-3 \right)-{{\left( x-3 \right)}^{2}}=0$
$\left( x-3 \right)\left( 4-x \right)=0$
$x\in \left\{ 3;4 \right\}$.
b) Ta có: ${{x}^{3}}+\dfrac{3}{2}{{x}^{2}}+\dfrac{3}{4}x+\dfrac{1}{8}=\dfrac{1}{64}$
${{\left( x+\dfrac{1}{2} \right)}^{3}}={{\left( \dfrac{1}{4} \right)}^{3}}$
$x+\dfrac{1}{2}=\dfrac{1}{4}$
$x=\dfrac{-1}{4}$.
Bài 3. (1 điểm) Người ta dùng máy ảnh để chụp một người có chiều cao $AB = 1,5$ m (như hình vẽ).
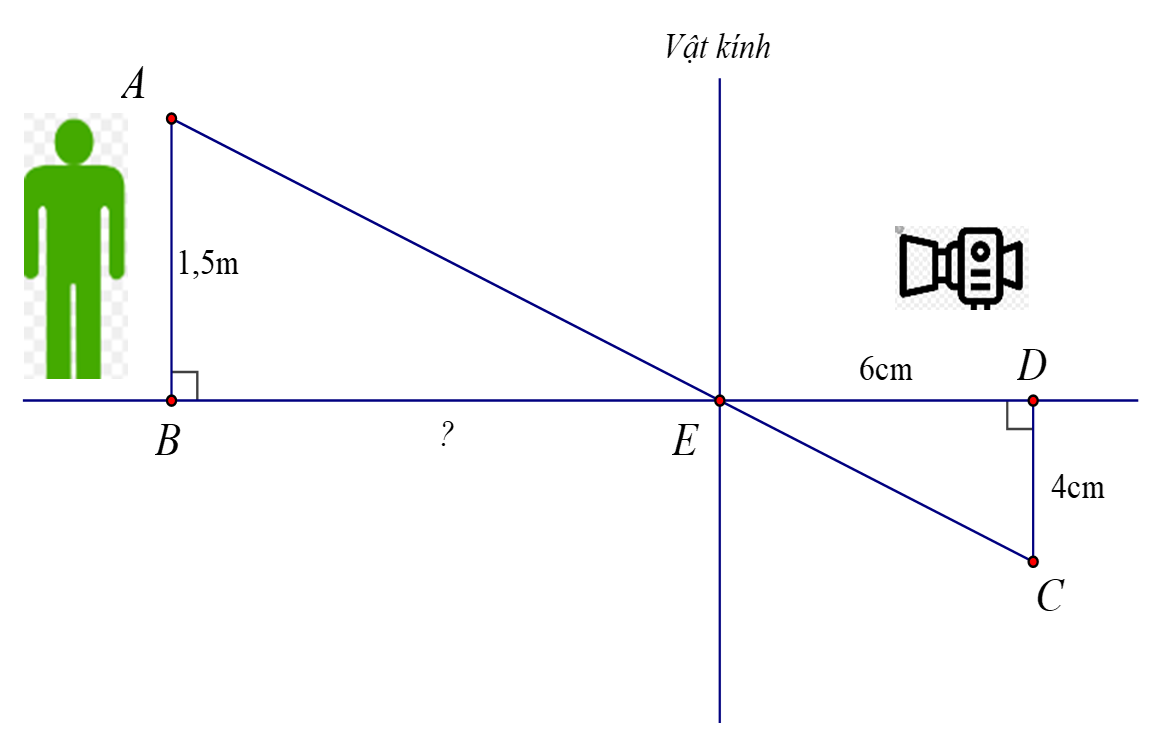
Sau khi rửa phim thấy ảnh $CD$ cao $4$ cm. Biết khoảng cách từ phim đến vật kính của máy ảnh lúc chụp là $ED = 6$ cm. Hỏi người đó đứng cách vật kính máy ảnh một đoạn $BE$ bao nhiêu cm?
Hướng dẫn giải:
Đổi đơn vị: $1,5$ m $= 150$ cm.
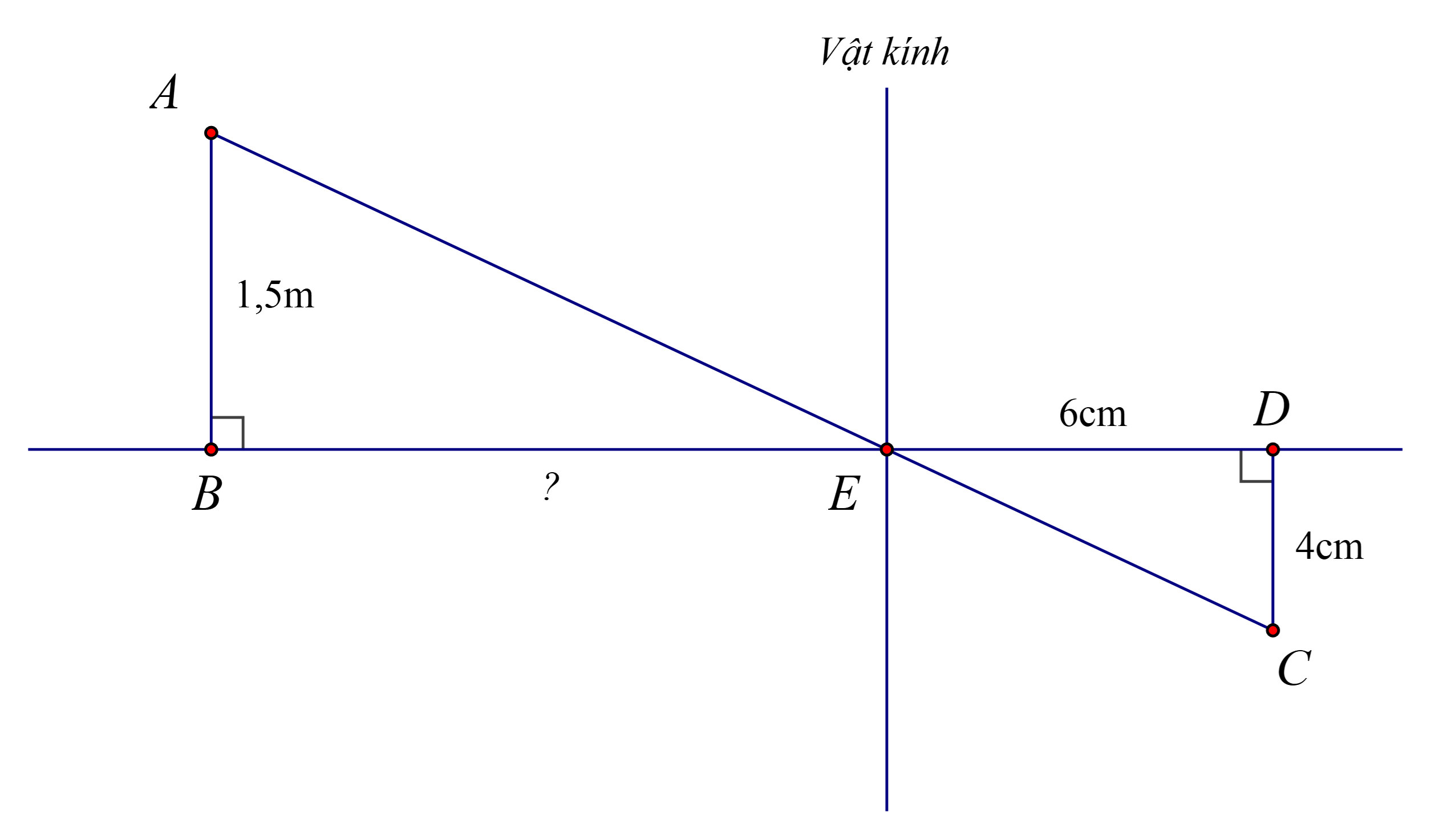
Ta có $AB$ // $CD$ (cùng vuông góc $BD$) suy ra $\dfrac{EB}{ED}=\dfrac{AB}{DC}$ (định lí Thalès)
Suy ra $EB=\dfrac{AB.ED}{DC}=\dfrac{150.6}{4}=225$ (cm).
Vậy người đứng cách vật kính máy ảnh là $225$ cm.
Bài 4. (1 điểm) Cho hình thang ${ABCD}$ với $AB$ // $CD$ có hai đường chéo ${AC}$, ${BD}$ cắt nhau tại ${O}$ và đường thẳng qua ${O}$ song song với đáy cắt các cạnh bên tại ${AD}$ và ${BC}$ theo thứ tự tại ${M}$ và ${N}$. Chứng minh ${OM=ON}$.
Hướng dẫn giải:
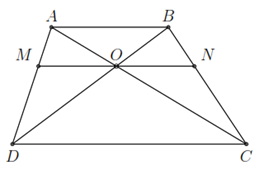
Xét $\Delta ADC$ có $MO$ // $DC$ nên theo định lí Thalès ta có
${\dfrac{OM}{DC}=\dfrac{OA}{AC}}$. (1)
Xét $\Delta BCD$ có $ON$ // $CD$ nên theo định lí Thalès ta có
${\dfrac{ON}{CD} = \dfrac{BN}{BC}}$. (2)
Xét $\Delta CAB$ có $ON$ // $CD$ nên theo định lí Thalès ta có
${\dfrac{BN}{BC} = \dfrac{AO}{AC}}$. (3)
Từ ${(1)}$, ${(2)}$, ${(3)}$ suy ra ${\dfrac{OM}{DC}=\dfrac{OA}{AC}=\dfrac{BN}{BC}=\dfrac{ON}{CD}}$.
Suy ra ${OM=ON}$.
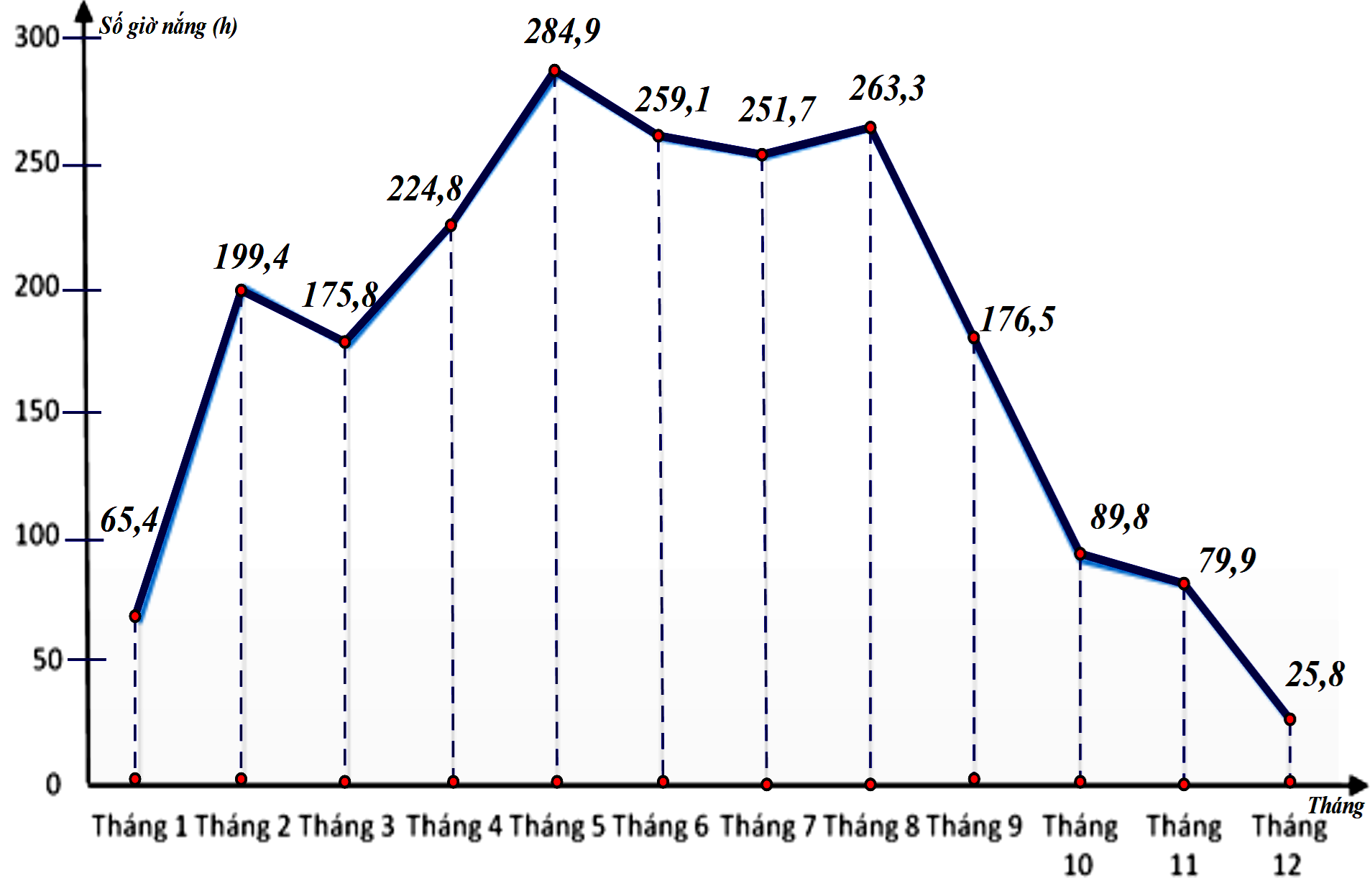
Bài 5. (1 điểm) Thống kê số giờ nắng của các tháng trong năm 2022 của T.P Huế từ tháng 1 đến tháng 12 lần lượt là: 65,4; 199,4; 175,8; 224,8; 284,9; 259,1; 251,7; 263,3; 176,5; 89,8; 79,9; 25,8 (đơn vị: giờ).
(Nguồn: Tổng cục thống kê)
Hoàn thành biểu đồ đoạn thẳng biểu diễn số giờ nắng của các tháng trong năm 2022 của T.P Huế.
Hướng dẫn giải: