Bài học cùng chủ đề
Báo cáo học liệu
Mua học liệu
Mua học liệu:
-
Số dư ví của bạn: 0 coin - 0 Xu
-
Nếu mua học liệu này bạn sẽ bị trừ: 2 coin\Xu
Để nhận Coin\Xu, bạn có thể:

Phần tự luận (6,5 điểm) SVIP
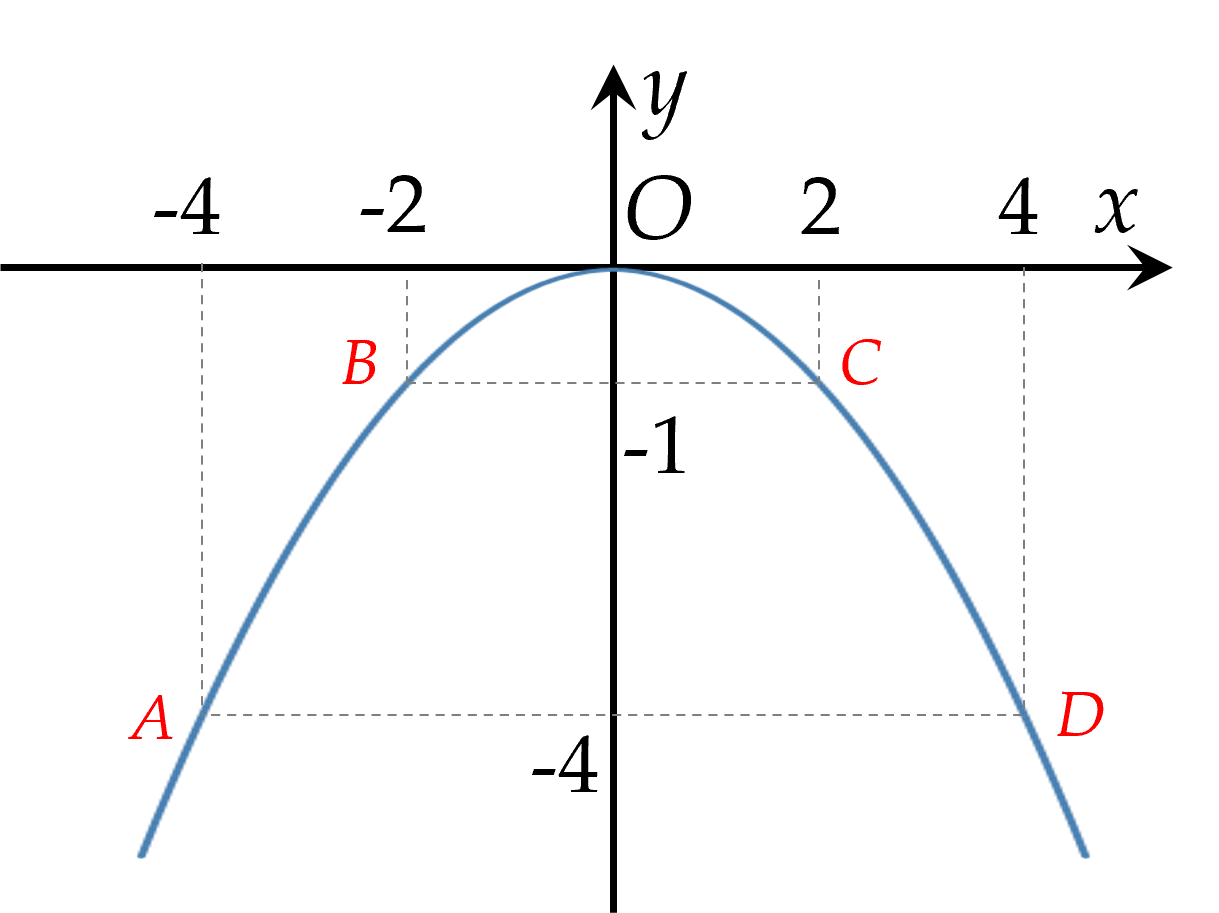
1) (0,5 điểm) Vẽ đồ thị hàm số $y=-\dfrac14x^2$.
2) (1,5 điểm) Cho phương trình $x^2-2mx+m^2-1=0$ (m là tham số) (1)
a) Giải phương trình (1) khi $m=-3$.
b) Tìm $m$ để phương trình (1) có hai nghiệm phân biệt $x_1; \, x_2$ thỏa mãn hệ thức: $(1+x_1)(2-x_2)+(1+x_2)(2-x_1)=x_{1}^{2}+x_{2}^{2}-x_1x_2-2$.
Hướng dẫn giải:
1) Bảng giá trị của $y$ tương ứng với giá trị của $x$ như sau:
| $x$ | $-4$ | $-2$ | $0$ | $2$ | $4$ |
| $y = -\dfrac14x^2$ | $-4$ | $-1$ | $0$ | $-1$ | $-4$ |
Vẽ các điểm $A( -4;-4 ),$ $B( -2;-1 )$, $O( 0;0 ),$ $C( 2;-1 ),$ $D( 4;-4 )$ thuộc đồ thị hàm số $y=-\dfrac14x^2$ trong mặt phẳng $Oxy$.
Vẽ đường parabol đi qua các điểm trên, ta nhận được đồ thị của hàm số $y=-\dfrac14x^2$.
2a) Với $m=-3$, phương trình (1) trở thành: $x^2+6x+8=0$
Tính $\Delta = 6^2-4.1.8=36-32=4>0$
Vậy phương trình có hai nghiệm phân biệt: $x_1=\dfrac{-6+\sqrt{4}}{2.1}=-2,\,\,x^2=\dfrac{-6-\sqrt{4}}{2.1}=-4$
Vậy với $m=-3$, tập nghiệm của phương trình là: $S=\left\{ -2;-4 \right\}$
2b) Xét phương trình: $x^2-2mx+m^2-1=0$ (1)
Tính $\Delta =(-2m)^2-4(m^2-1)=4m^2-4m^2+4=4>0$
Vậy phương trình (1) có hai nghiệm phân biệt $x_1, \, x^2$.
Theo định lí Viète: $x_1+x^2=2m$ và $x_1x^2=m^2-1$
Theo đề bài, ta có: $(1+x_1)(2-x^2)+(1+x^2)(2-x_1)=x_{1}^{2}+x_{2}^{2}-x_1x^2-2$
$4-2x_1x^2+x_{1}^{2}+x_{2}^{2}=x_{1}^{2}+x_{2}^{2}-x_1x^2-2$
$( x_1+x^2)^2-(x_1+x^2)-x_1x^2-6=0$
$4m^2-2m-( m^2-1 )-6=0$
$3m^2-2m-5=0$
Giải phương trình bậc hai ta được: $m=-1$ hoặc $m=\dfrac{5}{3}$.
(1 điểm) Một cơ sở sản xuất lập kế hoạch làm $600$ sản phẩm trong một thời gian nhất định. Do cải tiến kĩ thuật, năng suất mỗi ngày tăng $10$ sản phẩm. Vì thế không những hoàn thành sớm $1$ ngày, mà còn vượt mức $100$ sản phẩm. Theo kế hoạch mỗi ngày phải làm bao nhiêu sản phẩm?
Hướng dẫn giải:
Gọi năng suất dự kiến là $x$ (sản phẩm/ngày, $x > 0$)
Năng suất thực tế là: $x + 10$ (sản phẩm/ngày)
Thời gian làm theo kế hoạch là: $\dfrac{600}{x}$ (ngày)
Thời gian làm thực tế là: $\dfrac{700}{x+10}$ (ngày)
Theo đề bài, ta có phương trình: $\dfrac{600}{x}-\dfrac{700}{x+10}=1$
Giải phương trình: $600(x+10)-700x=x(x+10)$
$600x+6 \, 000-700x=x^2+10x$
$x^2+10x+110x-6 \, 000=0$
$x^2+110x-6 \, 000=0$
Giải phương trình bậc hai: $x_1=40$ (thỏa mãn điều kiện) hoặc $x_2=-150$ (loại)
Vậy theo dự định mỗi ngày phải làm $40$ sản phẩm.
(3 điểm) Cho tam giác $ABC$ vuông tại $A$, đường cao $AH$, $M$ là trung điểm của $AC$. Lấy $E$ là hình chiếu của $A$ trên $BM$.
a) Chứng minh $A$, $E$, $H$, $B$ cùng nằm trên một đường tròn.
b) Chứng minh $BE.BM=BH.BC$.
c) Đường thẳng đi qua $M$ và vuông góc với $BC$, cắt tia $AE$ tại $K$. Chứng minh $HM^2=ME.MB$ và tính số đo góc $MHK$.
Hướng dẫn giải:

a) Gọi $O$ là trung điểm của $AB$.
Xét $\Delta AHB$ vuông tại $H$ ($AH \bot BC$), có $HO$ là đường trung tuyến ứng với cạnh huyền $AB$.
Suy ra $HO=\dfrac{AB}{2}$ (tính chất đường trung tuyến ứng với cạnh huyền trong tam giác vuông)
Do đó $OA=OB=HO=\dfrac{AB}{2}$
Suy ra $A$, $B$, $H$ cùng thuộc đường tròn $\Big( O; \dfrac{AB}{2} \Big)$.
Chứng minh tương tự, suy ra $A$, $E$, $B$ cũng thuộc đường tròn $\Big( O;\dfrac{AB}{2} \Big)$.
Suy ra bốn điểm $A$, $E$, $H$, $B$ cùng thuộc đường tròn $\Big( O;\dfrac{AB}{2} \Big)$.
b) Xét $\Delta BAE$ và $\Delta BMA$ có:
$\widehat{BEA}=\widehat{BAM}=90^\circ$
$\widehat{ABE}$ chung
Suy ra $\Delta BAE \backsim \Delta BMA$ (g.g)
Suy ra $\dfrac{BA}{BM}=\dfrac{BE}{BA}$ hay $AB^2=BE.BM$ (1)
Chứng minh tương tự, ta có: $\Delta BAH \backsim \Delta BCA$ (g.g)
Suy ra $\dfrac{BA}{BC}=\dfrac{BH}{BA}$ hay $AB^2=BH.BC$ (2)
Từ (1) và (2) suy ra $BE . BM = BH . BC$ (điều phải chứng minh).
c) Xét $\Delta AHC$ vuông tại $H$, $HM$ là trung tuyến ứng với cạnh huyền $AC$ nên $HM=MA=MC=\dfrac{1}{2}AC$.
Xét $\Delta MAE$ và $\Delta MBA$ có:
$\widehat{MEA}=\widehat{MAB}=90^\circ$
$\widehat{AMB}$ chung
Suy ra $\Delta MAE \backsim \Delta MBA$ (g.g)
Suy ra $\dfrac{MA}{MB}=\dfrac{ME}{MA}$ hay $MA^2=ME.MB$.
Do đó $HM^2=ME.MB$ (3) (điều phải chứng minh).
Gọi $I$ là giao điểm của $MK$ và $HC$.
Xét $\Delta MBI$ và $\Delta MEK$ có:
$\widehat{MBI}=\widehat{MEK}=90^\circ$
$\widehat{BMK}$ chung
Suy ra $\Delta MBI\backsim \Delta MEK$ (g.g)
Suy ra $\dfrac{MI}{ME}=\dfrac{MB}{MK}$ hay $MI . MK = ME . MB$ (4).
Từ (3) và (4) suy ra $MI.MK=HM^2$ hay $\dfrac{HM}{MI}=\dfrac{MK}{HM}$.
Xét $\Delta MIH$ và $\Delta MHK$ có:
$\dfrac{HM}{MI}=\dfrac{MK}{HM}$
$\widehat{HMK}$ chung
Suy ra $\Delta MIH \backsim \Delta MHK$ (c.g.c).
Do đó $\widehat{MHK}=90^\circ$.
(0,5 điểm) Giải phương trình $x^2+6x+2=(2x+2)\sqrt{x^2+5}$.
Hướng dẫn giải:
$x^2+6x+2=(2x+2)\sqrt{x^2+5}$
$x^2+5+6x-3-(2x+2)\sqrt{x^2+5}=0$
$x^2+5+3(2x-1)-(2x-1)\sqrt{x^2+5}-3\sqrt{x^2+5}+5=0$
$\left( \sqrt{x^2+5}-2x+1 \right)\left( \sqrt{x^2+5}-3 \right)=0$
$\left[ \begin{aligned} & \sqrt{x^2+5}=2x-1 \\ & \sqrt{x^2+5}=3 \\ \end{aligned} \right.$
Giải ra ta được $x=2$ hoặc $x=-2$.
Vậy phương trình có tập nghiệm là $S=\left\{ -2;2 \right\}$.
