Phần tự luận (4 điểm) SVIP

Hướng dẫn giải:

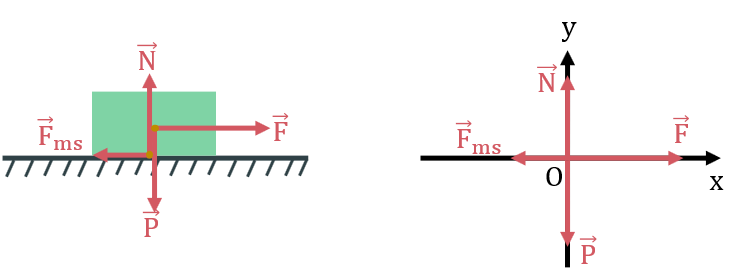
Các lực tác dụng lên vật: trọng lực \(\overrightarrow{P}\), phản lực \(\overrightarrow{N}\), lực kéo \(\overrightarrow{F}\), lực ma sát trượt \(\overrightarrow{F}_{ms}\)

Áp dụng định luật 2 Newton cho chuyển động của vật theo hai trục Ox, Oy:

\(\left\{{}\begin{matrix}F_x=F-F_{ms}=ma\\F_y=N-P=0\end{matrix}\right.\)

\(\Rightarrow N=P=mg=12.9,8=117,6\) N

\(F_{ms}=\mu.N=0,2.117,6=23,52\) N

\(\Rightarrow a=\dfrac{F-F_{ms}}{m}=\dfrac{30-23,52}{12}=0,54\) m/s²

Vậy gia tốc có độ lớn 0,54 m/s² và hướng theo chiều chuyển động của thùng.

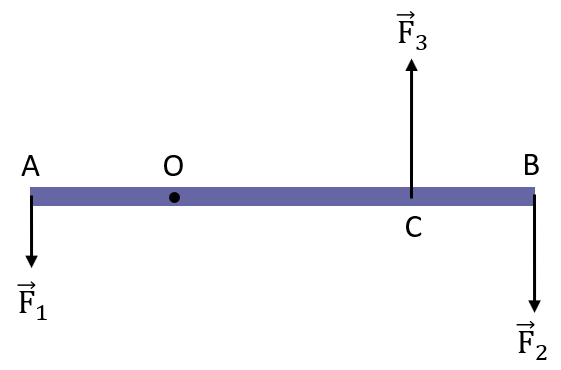
Hướng dẫn giải:

AB = 4 m; OA = 1 m; OB = 3 m

F₁ = 20 N; F₂ = 100 N; F₃ = 160 N

Theo quy tắc moment lực (thanh AB nằm cân bằng khi tổng các moment lực có xu hướng làm vật quay theo chiều kim đồng hồ bằng với tổng các moment lực có xu hướng làm vật quay ngược chiều kim đồng hồ), ta có:

\(M_A+M_C=M_B\)

\(\Rightarrow F_1.OA+F_3.OC=F_2.OB\)

\(\Rightarrow OC=\dfrac{F_2.OB-F_1.OA}{F_3}=\dfrac{100.3-20.1}{160}=1,75\) m

Hướng dẫn giải:

\(\text{v}_0=36km/h=10m/s\)

Quãng đường vật đi được trong 3 giây đầu tiên là: \(s_3=\text{v}_0t_3+\dfrac{1}{2}at_3^2=\text{v}_0.3+\dfrac{1}{2}.a.\left(3^2\right)=3\text{v}_0+\dfrac{9}{2}a\)

Quãng đường vật đi được trong 4 giây đầu tiên là: \(s_4=\text{v}_0t_4+\dfrac{1}{2}at_4^2=\text{v}_0.4+\dfrac{1}{2}.a.\left(4^2\right)=4\text{v}_0+8a\)

Quãng đường vật đi trong giây thứ 4 là: \(\Delta s=s_4-s_3=\text{v}_0+\dfrac{7}{2}a\)

\(\Rightarrow a=\dfrac{\Delta s-\text{v}_0}{\dfrac{7}{2}}=\dfrac{13,5-10}{\dfrac{7}{2}}=1\) m/s²