Bài học cùng chủ đề
Báo cáo học liệu
Mua học liệu
Mua học liệu:
-
Số dư ví của bạn: 0 coin - 0 Xu
-
Nếu mua học liệu này bạn sẽ bị trừ: 2 coin\Xu
Để nhận Coin\Xu, bạn có thể:

Phần tự luận (6,5 điểm) SVIP
Bài 1. (1,5 điểm)
1) Tìm $a$ biết đồ thị hàm số $y =(a-1)x^2$ đi qua điểm $A(1;-2)$.
2) Một vật rơi ở độ cao so với mặt đất là $80$ m. Quãng đường chuyển động $S$ (đơn vị tính bằng mét) của vật rơi phụ thuộc vào thời gian $t$ (đơn vị tính bằng giây) được cho bởi công thức $S = 5t^2$.
a) Sau khoảng thời gian $3$ giây, vật này cách mặt đất bao nhiêu mét?
b) Sau thời gian bao lâu thì vật tiếp đất?
Hướng dẫn giải:
1) Do đồ thị hàm số $y =(a-1)x^2$ đi qua điểm $A(1;-2)$
Suy ra thay $x =-1;\,y = -2$ vào hàm số ta được $(a-1).1^2 = -2$.
$a-1=-2$
$a=-1$
Vậy $a = -1$ thì đồ thị hàm số đi qua điểm $A(1;-2)$.
2)
a) $t=3$ (s) thì $S=5.32 = 45$ (m)
Sau thời gian $3$ giây vật cách mặt đất là: $80-45 = 35$ (m)
b) Vật tiếp đất khi $S=80$ m.
Ta có: $5t^2=80$
$t^2 = 16$
Suy ra $t=4$ (s) (Vì $t>0$)
Vậy sau thời gian $4$ giây thì vật tiếp đất.
Bài 2. (1 điểm)
Cho phương trình $x^2-5x+m-2=0$ (1), với $m$ là tham số. Tìm $m$ để phương trình (1) có hai nghiệm phân biệt $x_1,\, x_2$ thỏa mãn hệ thức: $2\Big( \dfrac{1}{\sqrt{x_1}}+\dfrac{1}{\sqrt{x_2}} \Big)=3$.
Hướng dẫn giải:
Để (1) có $2$ nghiệm phân biệt thì $\Delta >0$
$5^2 - 4(m-2) > 0$
$33-4m>0$
$m<\dfrac{33}{4}$.
Giả sử hai nghiệm của phương trình (1) là $x_1, \, x_2$, theo hệ thức Viète, ta có
$\left\{ \begin{aligned} & x_1 + x_2 =5 \\ & x_1.x_2=m-2 \end{aligned} \right.$
Để (1) có hai nghiệm phân biệt dương, ta có:
$\left\{ \begin{aligned} & m<\dfrac{33}{4} \\ & m-2>0 \end{aligned} \right.$
Suy ra $ \left\{ \begin{aligned} & m<\dfrac{33}{4} \\ & m>2 \end{aligned} \right.$
Hay $ 2<m<\dfrac{33}{4}$.
Ta có: $2\Big( \dfrac{1}{\sqrt{x_1}}+\dfrac{1}{\sqrt{x_2}} \Big)=3$
$2\Big( \dfrac{\sqrt{x_1}+\sqrt{x_2}}{\sqrt{x_1.x_2}} \Big)=3$
$2(\sqrt{x_1}+\sqrt{x_2})=3\sqrt{x_1.x_2}$
$4( x_1+x_2+2\sqrt{x_1.x_2})=9x_1.x_2$
Suy ra $4.(5+2\sqrt{m-2})=9(m-2)$
$9(m-2)-8\sqrt{m-2}-20=0$
Đặt $\sqrt{m-2}=t, \,t\ge 0$, ta có phương trình $9t^2-8t-20=0.$
Giải phương trình, ta có $t_1=2$ (thỏa mãn); $t_2=-\dfrac{10}{9}$ (loại).
Với $t_1=2$:
$\sqrt{m-2}=2$
$m=6$ (thỏa mãn).
Vậy giá trị của $m$ là $m = 6$.
Bài 3. (1 điểm)
Một công ty điều một số xe tải để chở $67,5$ tấn hàng. Khi đến kho hàng thì có $3$ xe bị hỏng nên để chở hết số hàng thì mỗi xe còn lại phải chở thêm $0,25$ tấn so với dự định ban đầu. Số xe được điều đến chở hàng là bao nhiêu? Biết rằng khối lượng hàng mỗi xe chở là như nhau.
Hướng dẫn giải:
Gọi $x$ là số xe được điều đến chở hàng lúc đầu ($x \in \mathbb{Z}, x > 3$).
Số xe lúc sau là $x-2$ (xe).
Số hàng mỗi xe phải chở lúc đầu là $\dfrac{67,5}{x}$ (tấn).
Số hàng mỗi xe phải chở lúc sau là $\dfrac{67,5}{x-3}$ (tấn)
Ta có phương trình: $\dfrac{67,5}{x-3} -\dfrac{67,5}{x} = \dfrac{1}{4} $
Giải phương trình trên, ta được $x_1 =30$ (thoả mãn); $x_2 =- 27$ (loại).
Vậy công ty đã điều $30$ xe đến chở hàng.
Bài 4. (2,0 điểm)
Cho đường tròn $(O)$ đường kính $AB$. Dây cung $MN$ vuông góc với $AB$, $(AM < BM)$. Hai đường thẳng $BM$ và $NA$ cắt nhau tại $K$. Gọi $H$ là chân đường vuông góc kẻ từ $K$ đến đường thẳng $AB$.
a) Chứng minh tứ giác $AHKM$ nội tiếp trong một đường tròn.
b) Chứng minh rằng $NB .HK = AN .HB$.
c) Chứng minh $HM$ là tiếp tuyến của đường tròn $(O)$.
Hướng dẫn giải:
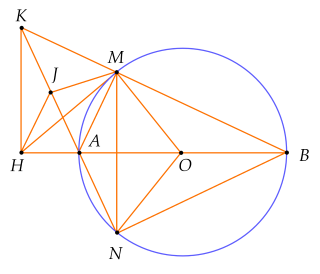
a) Gọi $J$ là trung điểm của $AK$
$\Delta AMK$ vuông tại $M$, có $MJ$ là trung tuyến ứng với cạnh huyền nên $JA=JK=JM=\dfrac12 AK$ (1)
$\Delta AHK$ vuông tại $H$, có $HJ$ là trung tuyến ứng với cạnh huyền nên $HA=HK=HJ=\dfrac12 AK$ (2)
Từ (1) và (2), suy ra $JA=JK=JM=JH$, suy ra bốn điểm $A, K , M, H$ cùng thuộc đường tròn tâm $J$ hay tứ giác $AHKM$ nội tiếp đường tròn $(J)$.
b) Xét $\Delta ANB$ và $\Delta KHB$ có:
$\widehat{ANB} = 90^\circ$ (góc nội tiếp chắn nửa đường tròn)
Suy ra $\widehat{ANB} = \widehat{KHB} = 90^\circ$;
Xét $\Delta OMN$ cân tại $O$, có $OA$ là đường cao nên $OA$ là đường phân giác của góc $MON$.
Suy ra $\widehat{MOA} = \widehat{NOA}$ hay $\widehat{ABN} = \widehat{KBH}$
Suy ra $\Delta ANB \backsim \Delta KHB$ (g-g)
Suy ra $\dfrac{AN}{NB} = \dfrac{KH}{KB}$ hay $NB.HK = AN. HB$ (điều phải chứng minh).
c) Ta có $HM$ giao với đường tròn $(O)$ tại $M$ , ta phải chứng minh $HM \bot OM$.
Thật vậy:
Tứ giác $AHKM$ nội tiếp
Suy ra $\widehat{HMK} = \widehat{HAK}$ (hai góc nội tiếp cùng chắn $HK$);
$\widehat{HAK} = \widehat{NAB}$ (hai góc đối đỉnh);
Mà $\Delta OMN$ cân tại $O$, có $OA$ là đường cao nên $OA$ là đường trung trực của $MN$
Suy ra $AB$ là đường trung trực của $MN$
Suy ra $MB = NB$
Suy ra $\widehat{NAB} = \widehat{MAB}$
$\widehat{MAB} = \widehat{OMA}$ ($\Delta OAM$ cân tại $O$);
$\widehat{HMK} = \widehat{OMA} (= \widehat{HAK} = \widehat{NAB} = \widehat{MAB}$)
Suy ra $\widehat{HMK} + \widehat{HMA} = \widehat{OMA} + \widehat{HMA}$;
Mà $\widehat{HMK} + \widehat{HMA} = \widehat{AMK} = 90^\circ$ (kề bù với $\widehat{AMB} = 90^\circ$, góc nội tiếp chắn nửa đường tròn $(O)$)
Suy ra $\widehat{OMA} + \widehat{HMA} = 90^\circ$ hay $\widehat{HMO} = 90^\circ$ nên $HM \bot OM$ tại $M$
Do đó $HM$ là tiếp tuyến của $(O)$.
Bài 5. (1 điểm)
Bạn Giang chọn một đoạn văn gồm $100$ từ và đếm số chữ cái trong mỗi từ của đoạn văn này cho kết quả như trong biểu đồ sau:
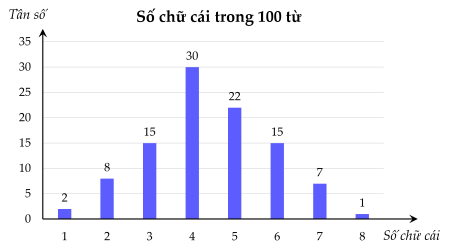
a) Lập bảng tần số tương đối cho dữ liệu được biểu diễn trên biểu đồ.
b) Tìm ước lượng cho xác suất một từ có nhiều hơn $5$ chữ cái.
Hướng dẫn giải:
a) Cỡ mẫu $n = 2 + 8 + 15 + 30 + 22 + 15 + 7 + 1 = 100$.
Bảng tần số tương đối cho dữ liệu được biểu diễn trên biểu đồ là:
| Số chữ cái | $1$ | $2$ | $3$ | $4$ | $5$ | $6$ | $7$ | $8$ |
| Tần số tương đối | $2\%$ | $8\%$ | $15\%$ | $30\%$ | $22\%$ | $15\%$ | $7\%$ | $1\%$ |
b) Xác suất một từ có nhiều hơn $5$ chữ cái là:
$15\% + 7\% + 1\% = 23\%$.
Vậy ước lượng cho xác suất một từ có nhiều hơn $5$ chữ cái khoảng $ 23\%$.
