Phần tự luận SVIP

Hướng dẫn giải:

Gọi $A,B$ là hai điểm tại hai vị trí chân thang và $C,D$ là hai điểm tại hai vị trí ngọn thang, $EF$ là đường chân tường.

Ta có $EF//AB$ nên $(EF,AC)=(AB,AC)=\widehat{CAB}$.

Kẻ $CH\bot AB$ tại $H$, $DK\bot AB$ tại $K$.

Ta có $CDKH$ là hình chữ nhật nên$CH=DK$, $CD=HK$.

Xét $\Delta CHA$ và $\Delta DKB$ có:

$\left\{ \begin{aligned}& CA=DB\\&\widehat{CHA}=\widehat{DKB}=90^\circ \\& CH=DK \\\end{aligned} \right.$

Nên $\Delta CHA=\Delta DKB$ (c – g – c).

Suy ra $AH=KB$.

Khi đó $AH=\dfrac{AB-CD}{2}=10$ (cm) $=0,1$ (m).

Vì tam giác $ACH$ vuông tại $H$ nên

$\cos \widehat{CAH}=\dfrac{AH}{AC}=\dfrac{0,1}{6}=\dfrac{1}{60}$

$\widehat{CAH}\approx 89,05^\circ$.

Do đó, $\widehat{CAB}\approx 89,05^\circ$

Vậy góc tạo giữa đường thẳng chân tường và cạnh cột thang khoảng $89,05^\circ.$

Hướng dẫn giải:

Theo dự kiến, cần $24$ tháng để hoàn thành công trình. Vậy khối lượng công việc trên một tháng theo dự tính là: $\dfrac{1}{24}$ (công trình)

Khối lượng công việc của tháng thứ 2 là:

$T_2=\dfrac{1}{24}+0,04.\dfrac{1}{24}=\dfrac{1}{24}{(1+0,04 )^1}$

Khối lượng công việc của tháng thứ 3 là:

$T_3=\Big(\dfrac{1}{24}+0,04.\dfrac{1}{24}\Big )+0,04.\Big(\dfrac{1}{24}+0,04.\dfrac{1}{24} \Big)$

$=\dfrac{1}{24}.{{(1+0,04 )}^{2}}$

Như vậy khối lượng công việc của tháng thứ $n$ là: ${{T}_{n}}=\dfrac{1}{24}.{{(1+0,04 )}^{n-1}}$

Ta có: $\dfrac{1}{24}.{{(1+0,04 )}^{0}}+\dfrac{1}{24}.{{(1+0,04 )}^{1}}+...+\dfrac{1}{24}.{{(1+0,04 )}^{n-1}}=1$

$\Leftrightarrow \dfrac{1}{24}.\dfrac{1-{{(1+0,04 )}^{n}}}{1-(1+0,04 )}=1$

$\Leftrightarrow {{(1+0,04 )}^{n}}=\dfrac{49}{25}$

$\Leftrightarrow n={{\log }_{1+0,04}}\dfrac{49}{25}\approx 17,2$

Vậy công trình sẽ hoàn thành ở tháng thứ $18$ từ khi khởi công.

Hướng dẫn giải:

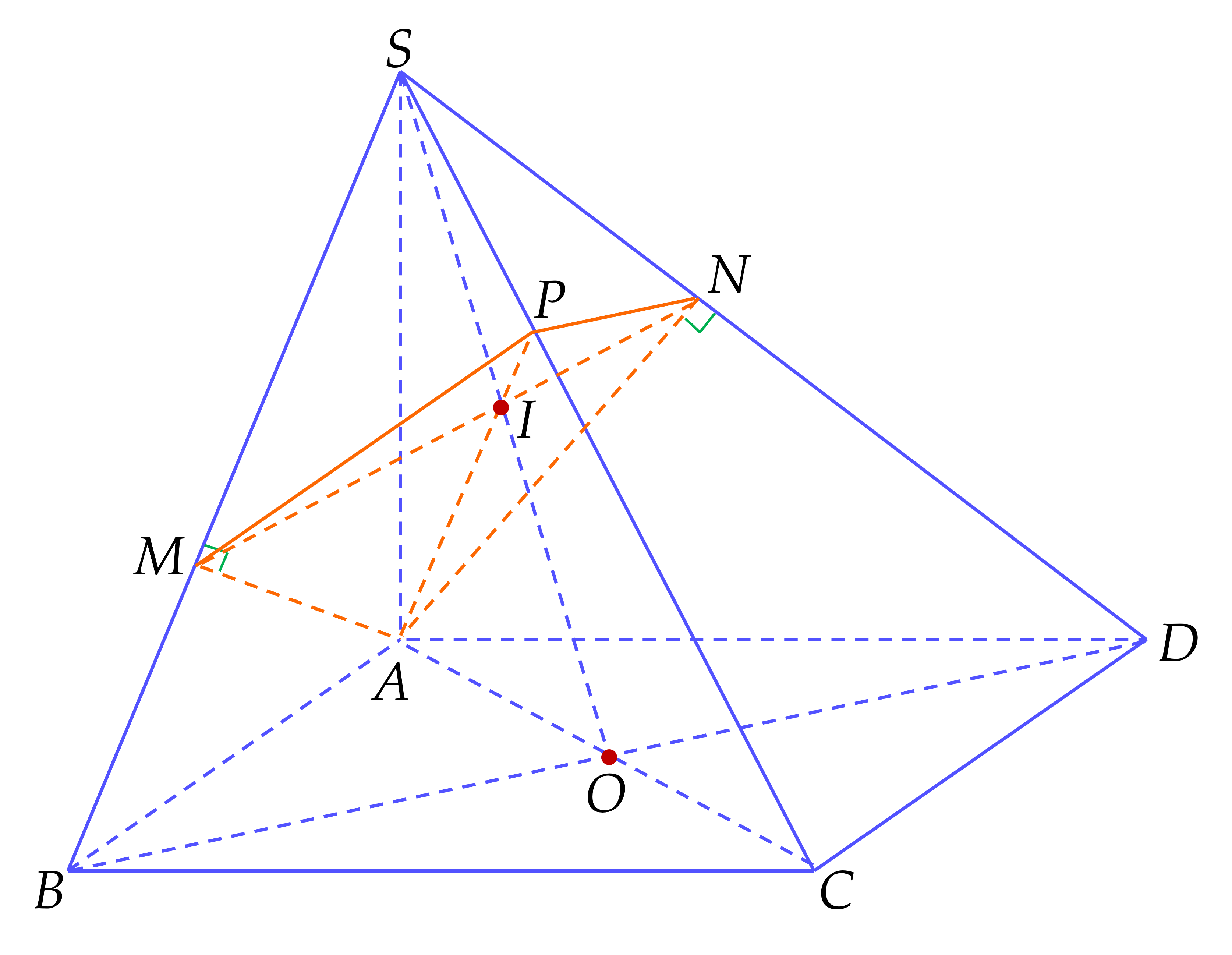
 Gọi $P=SC\cap (AMN )$; $O=AC\cap BD$

$\Rightarrow MN$; $AP$; $SO$ đồng quy tại $I$

Ta có: $\left\{ \begin{aligned}& SA\bot BC \\& AB\bot BC \\\end{aligned} \right.$

$\Rightarrow $$BC\bot (SAB )$

$\Rightarrow $$BC\bot AM$

Mà $AM\bot SB$ nên $AM\bot (SBC)$

$\Rightarrow $$AM\bot SC$

Ta có: $\left\{ \begin{aligned}& SA\bot CD \\& AD\bot CD \\\end{aligned} \right.$

$\Rightarrow $$CD\bot (SAD )$

$\Rightarrow $$CD\bot AN$

Mà $AN\bot SD$ nên $AN\bot (SCD )$

$\Rightarrow $$AN\bot SC$

Do đó $SC\bot (AMN)$

$\Rightarrow $$AP\bot SC$ và $PM$ là hình chiếu của $SM$ trên mặt phẳng $(AMN )$ hay $PM$ là hình chiếu của $SB$ trên mặt phẳng $(AMN )$

$\Rightarrow $$\widehat{(SB\,;\,(AMN ) )}=\widehat{(SB\,;\,PM )}=\widehat{SMP}$ (do tam giác $SMP$vuông tại $P$)

Ta có: $\dfrac{SP}{SC}=\dfrac{SA^2}{SC^2}=\dfrac{3}{5}$

$\Rightarrow SP=\dfrac{3}{5}.a\sqrt{5}$

$\dfrac{SM}{SB}=\dfrac{SA^2}{SB^2}=\dfrac{3}{4}$

$\Rightarrow SM=\dfrac{3}{2}.a$

$\tan \widehat{SMP}=\dfrac{SP}{PM}=\dfrac{3a\sqrt{5}}{5}:\dfrac{3}{2\sqrt{5}}a=2$.