Phần tự luận (3 điểm) SVIP

Hướng dẫn giải:

Trường hợp $1$: $m\,=\,0 $.

Bất phương trình trở thành $2x>0\Leftrightarrow x\,>\,0$.

Vậy $m\,=\,0$ không thoả yêu cầu bài toán.

Trường hợp $2$: $m\,\ne \,0\,$

Để bất phương trình nghiệm đúng $\forall x\in \mathbb{R}$ thì

$\left\{ \begin{aligned}  & a>0 \\  & \Delta <0 \end{aligned} \right.\Leftrightarrow \left\{ \begin{aligned}  & m>0 \\  & (m-1)^2-4m^2<0 \end{aligned} \right.$

$\Leftrightarrow \left\{ \begin{aligned}  & m>0 \\  & -3m^2-2m+1<0 \end{aligned} \right.\Leftrightarrow \left\{ \begin{aligned}  & m>0 \\  & \left[ \begin{aligned}  & m<-1 \\  & m>\dfrac{1}{3} \end{aligned} \right. \end{aligned} \right.\Leftrightarrow m>\dfrac{1}{3}$.

Vậy với $m>\dfrac{1}{3}$ thì bất phương trình nghiệm đúng với mọi $x$.

Hướng dẫn giải:

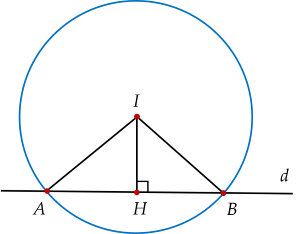
Gọi $H$ là trung điểm của $AB.$ Suy ra $IH \bot AB$.

$AH=\dfrac{1}{2}AB=5.$

Ta có $IH=d(I,d)=\dfrac{\left|4.(-4)-3.2-3 \right|}{\sqrt{4^2+(-3)^2}}=5$

Khi đó, bán kính của đường tròn cần tìm: $R=IA=\sqrt{IH^2+AH^2}=5\sqrt{2}.$

Phương trình đường tròn cần tìm: $(x+4)^2+(y-2)^2=50.$

Hướng dẫn giải:

Vận tốc của tàu thủy là $\left| \overrightarrow{v} \right|=\sqrt{{{4}^{2}}+{{(-3)}^{2}}}=5$(km/h)

Quãng đường tàu đi được sau $5$ giờ là $5.5 = 25$ (km)

Tàu chuyển động trên đường thẳng có phương trình $\Delta :\left\{ \begin{aligned}  & x=2+4t \\  & y=3-3t \end{aligned} \right.(t\in \mathbb{R})$

Gọi tọa độ của tai tại thời điểm bất kì là $B\Rightarrow B\left( 2+4t;3-3t \right)$

$\overrightarrow{AB} = \left( 4t;-3t \right)$

$\Rightarrow AB=\sqrt{{{(4t)}^{2}}+{{(-3t)}^{2}}}=\left| 5t \right|$

$\Rightarrow \left| 5t \right|=25$

$\Leftrightarrow t=\pm 5$

Vì tàu chạy theo hướng của $\overrightarrow{v}=\left( 4;-3 \right)$nên tọa độ của tàu là $B\left( 22;-12 \right).$

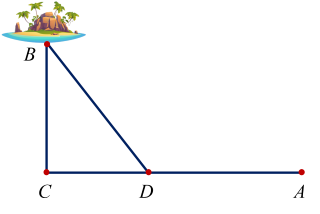
Hướng dẫn giải:

Đặt $AD=x$ km, $0<x<9$, $CD=9-x$; $BD=\sqrt{36+{{\left( 9-x \right)}^{2}}}$

Giá thành lắp đặt là: $50\ 000x+\sqrt{36+{{\left( 9-x \right)}^{2}}}.130\ 000=1\ 170\ 000$

$\Leftrightarrow 5x+13\sqrt{36+{{\left( 9-x \right)}^{2}}}=117$

$\Leftrightarrow 13\sqrt{36+{{\left( 9-x \right)}^{2}}}=117-5x$

$\Leftrightarrow \left\{   \begin{aligned}  & 117-5x\ge 0 \\  & 169(36+81-18x+{{x}^{2}})=13\ 689-1\ 170x+25{{x}^{2}} \end{aligned} \right.$

$\Leftrightarrow \left\{ \begin{aligned}  & x\le \dfrac{117}{5} \\  & 144x^2-1\, 872x+6\, 084=0 \end{aligned} \right.$

$\Leftrightarrow x=\dfrac{13}{2}$.

Vậy $AD=6,5$ km.