Phần tự luận (3 điểm) SVIP

Hướng dẫn giải:

a) Ta có $f(x)=x^2+2(m-1)x+m+5$ có $\Delta '=(m-1)^2-(m+5)=m^2-3m-4$

Lại có hệ số $a = 1 > 0$.

Để $f(x)$ luôn dương (cùng dấu hệ số $a$) với mọi $x\in \mathbb{R}$ thì $\Delta '<0$ $\Leftrightarrow {{m}^{2}}-3m-4<0$.

Xét tam thức $h(m)=m^2-3m-4$ có ${{\Delta }_{m}}=9-4.(-4)=25>0$ nên $h(m)$ có hai nghiệm là $m_1=-1$ và $m_2=4$.

Ta có bảng xét dấu của $h(m)$:

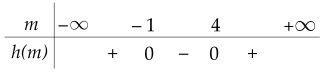
Do đó $h(m) < 0$ với mọi $x\in (-1;4)$

Hay $\Delta '<0$ với mọi $x\in (-1;4)$

Vậy $x\in (-1;4)$ thì tam thức bậc hai $f(x)=x^2+(m-1)x+m+5$ dương với mọi $x\in \mathbb{R}$.

b) Bình phương hai vế ta được: $2x^2-8x+4=x^2-4x+4$

$\Leftrightarrow x^2-4x=0$

Suy ra $x=0$ hoặc $x=4$

Thử lại nghiệm được $x=4$ thỏa mãn phương trình.

Vậy tập nghiệm $S = {4}$.

Hướng dẫn giải:

a)

$\cos \alpha =\left| \cos \left( \overrightarrow{{{n}_{\Delta }}};\overrightarrow{{{n}_{{{\Delta }_{1}}}}} \right) \right|=\dfrac{\left| 12.3+4.5 \right|}{5.13}=\dfrac{56}{65}$.

b) $(C)$ có tâm $I(-3; 2)$, bán kính $R=6$

Đường thẳng $d$ có dạng $3x-4y+m=0$ ($m$ khác $7$)

$d$ tiếp xúc $(C)$ khi và chỉ khi $d(I,d)=R \Leftrightarrow \dfrac{\left| -9-8+m \right|}{5}=6$.

Tìm được $m=47$(TM), $m=-13$ (TM)

Vậy có hai đường thẳng $d$ thỏa mãn là $3x-4y-13=0$ và $3x-4y-13=0$.

Hướng dẫn giải:

Kích thước của cả khung ảnh là $(17+2x)$ cm x $(25+2x)$ cm (Điều kiện: $x>0$)

Diện tích cả khung ảnh là: S = $(17+2x ).(25+2x)=4x^2+84x+425$

Để diện tích của cả khung ảnh lớn nhất là $513$ cm² thì  $S=4{{x}^{2}}+84x+425\le 513$

$\Rightarrow 4x^2+84x-88\le 0\Leftrightarrow -22\le x\le 1$. Vì $x>0$ nên $x\in (0;1]$

Vậy cần phải làm độ rộng viền khung ảnh tối đa $1$ (cm).