Bài học cùng chủ đề
Báo cáo học liệu
Mua học liệu
Mua học liệu:
-
Số dư ví của bạn: 0 coin - 0 Xu
-
Nếu mua học liệu này bạn sẽ bị trừ: 2 coin\Xu
Để nhận Coin\Xu, bạn có thể:

Phần tự luận (7 điểm) SVIP
a) (0,25 điểm) Tìm các tỉ số bằng nhau trong các tỉ số sau đây .
$7: 21 \,;\, \dfrac{1}{5}: \dfrac{1}{2} \,;\, \dfrac{1}{4}: \dfrac{3}{4} \,;\, 1,1: 3,2 \,;\, 1: 2,5$.
b) (0,25 điểm) Tìm ${x}$ trong tỉ lệ thức $\dfrac{5}{3}=\dfrac{x}{9}$.
Hướng dẫn giải:
a) $\dfrac{1}{5}: \dfrac{1}{2}=1: 2,5$.
b) $\dfrac{5}{3}=\dfrac{x}{9}$ suy ra $x=\dfrac{5.9}{3}=15$.
a) (0,25 điểm) Biết $a;c;e$ lần lượt tỉ lệ với $b;d;f$. Điền chữ thích hợp vào ô trống.
$\dfrac{a}{b}=\dfrac{\cdots}{d}=\dfrac{e}{f}=\dfrac{a+c+\ldots}{b+d+f}$
b) (0,25 điểm) Tìm 2 số ${x}, {y}$ biết : $\dfrac{x}{4}=\dfrac{y}{7}$ và ${x}+{y}=55$.
Hướng dẫn giải:
a) $\dfrac{a}{b}=\dfrac{c}{d}=\dfrac{e}{f}=\dfrac{a+c+e}{b+d+f}$.
b) $\dfrac{x}{4}=\dfrac{y}{7}=\dfrac{x+y}{4+7}=\dfrac{55}{11}=5$;
Suy ra $x=4.5=20 ; y=7.5=35$.
(1,0 điểm) Cho biết hai đại lượng $a$ và $b$ tỉ lệ nghịch với nhau và khi $a=3$ thì $b=-10$.
a) Tìm hệ số tỉ lệ.
b) Tìm giá trị của $a$ khi $b=2$.
Hướng dẫn giải:
a) Hệ số tỉ lệ $k= a.b = 3. (-10)=-30$.
b) Ta có: ${a} . {b}=-30$. Với ${a}=2$ suy ra $-30: 2=-15$.
(1,5 điểm)
Hai lớp 7A và lớp 7B quyên góp được một số sách tỉ lệ thuận với số học sinh của lớp, biết số học sinh của hai lớp lần lượt là $32$ và $36$. Lớp 7A quyên góp được ít hơn lớp 7B là $8$ quyển sách. Hỏi mỗi lớp quyên góp được là bao nhiêu quyển sách?
Hướng dẫn giải:
Gọi $x, y$ lần lượt là số sách quyên góp được của mỗi lớp $\left(x, y \in \mathbb N^*\right)$
Theo đầu bài ta có: $\dfrac{x}{32}=\dfrac{y}{36}$ và ${y}-{x}=8$
Theo tính chất của dãy tỉ số bằng nhau ta được:
$\dfrac{x}{32}=\dfrac{y}{36}=\dfrac{y-x}{36-32}=\dfrac{8}{4}=2$
Suy ra ${x}=32.2=64 ; {y}=36.2=72$
Vậy lớp 7A quyên góp được $64$ quyển.
Lớp 7B quyên góp được $72$ quyển.
(2,5 điểm) Cho hình vẽ.
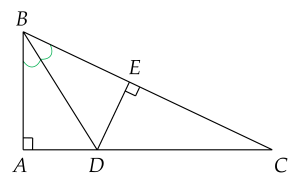
a) Chứng minh $\Delta {ABD}=\Delta {EBD}$.
b) Chứng minh $\Delta {ABE}$ là tam giác cân.
c) So sánh độ dài $BA$ và $BC$.
Hướng dẫn giải:
a) Xét $\Delta {ABD}$ và $\Delta {EBD}$, có:
$\widehat{{BAD}}=\widehat{{BED}}=90^{\circ}$
${BD}$ là cạnh huyền chung.
$\widehat{{ABD}}=\widehat{{EBD}}$
Vậy $\Delta {ABD}=\Delta {EBD}$ (cạnh huyền - góc nhọn)
b) Vi $\Delta {ABD}=\Delta {EBD}({cmt})$
Suy ra ${AB}={EB}$
Do đó : $\Delta A B E$ cân tại $B$.
c) Ta có ${BA}$ là đường vuông góc, ${BC}$ là đường xiên.
Suy ra ${BA}<{BC}$.
(1,0 điểm)
Tìm ${x}, {y}, {z}$ biết : $\dfrac{x}{10}=\dfrac{y}{5} ; \dfrac{y}{2}=\dfrac{z}{3}$ và ${x}+4 {z}=320$.
Hướng dẫn giải:
Ta có: $\dfrac{x}{10}=\dfrac{y}{5}$ và $\dfrac{y}{2}=\dfrac{z}{3}$
Suy ra $\dfrac{x}{20}=\dfrac{y}{10} ; \dfrac{y}{10}=\dfrac{z}{15}$
Suy ra $\dfrac{x}{20}=\dfrac{y}{10}=\dfrac{z}{15}=\dfrac{4 z}{60}=\dfrac{x+4 z}{20+60}=\dfrac{320}{80}=4$.
Suy ra $x=80;y=40;z=60$.
