Báo cáo học liệu
Mua học liệu
Mua học liệu:
-
Số dư ví của bạn: 0 coin - 0 Xu
-
Nếu mua học liệu này bạn sẽ bị trừ: 2 coin\Xu
Để nhận Coin\Xu, bạn có thể:
CHÚC MỪNG
Bạn đã nhận được sao học tập

Chú ý:
Thành tích của bạn sẽ được cập nhật trên bảng xếp hạng sau 1 giờ!
Parabol SVIP

Nếu video không chạy trên Zalo, bạn vui lòng Click vào đây để xem hướng dẫn
Lưu ý: Ở điểm dừng, nếu không thấy nút nộp bài, bạn hãy kéo thanh trượt xuống dưới.
Bạn phải xem đến hết Video thì mới được lưu thời gian xem.
Để đảm bảo tốc độ truyền video, OLM lưu trữ video trên youtube. Do vậy phụ huynh tạm thời không chặn youtube để con có thể xem được bài giảng.
Nội dung này là Video có điểm dừng: Xem video kết hợp với trả lời câu hỏi.
Nếu câu hỏi nào bị trả lời sai, bạn sẽ phải trả lời lại dạng bài đó đến khi nào đúng mới qua được điểm dừng.
Bạn không được phép tua video qua một điểm dừng chưa hoàn thành.
Dữ liệu luyện tập chỉ được lưu khi bạn qua mỗi điểm dừng.
Lưu ý: Ở điểm dừng, nếu không thấy nút nộp bài, bạn hãy kéo thanh trượt xuống dưới.
Bạn phải xem đến hết Video thì mới được lưu thời gian xem.
Để đảm bảo tốc độ truyền video, OLM lưu trữ video trên youtube. Do vậy phụ huynh tạm thời không chặn youtube để con có thể xem được bài giảng.
Nội dung này là Video có điểm dừng: Xem video kết hợp với trả lời câu hỏi.
Nếu câu hỏi nào bị trả lời sai, bạn sẽ phải trả lời lại dạng bài đó đến khi nào đúng mới qua được điểm dừng.
Bạn không được phép tua video qua một điểm dừng chưa hoàn thành.
Dữ liệu luyện tập chỉ được lưu khi bạn qua mỗi điểm dừng.
Theo dõi OLM miễn phí trên Youtube và Facebook:
Cho một điểm \(F\) cố định và một đường thẳng \(\Delta\) cố định không đi qua \(F\).
Đường parabol (hay parabol) là tập hợp các điểm \(M\) cách đều \(F\) và \(\Delta\). 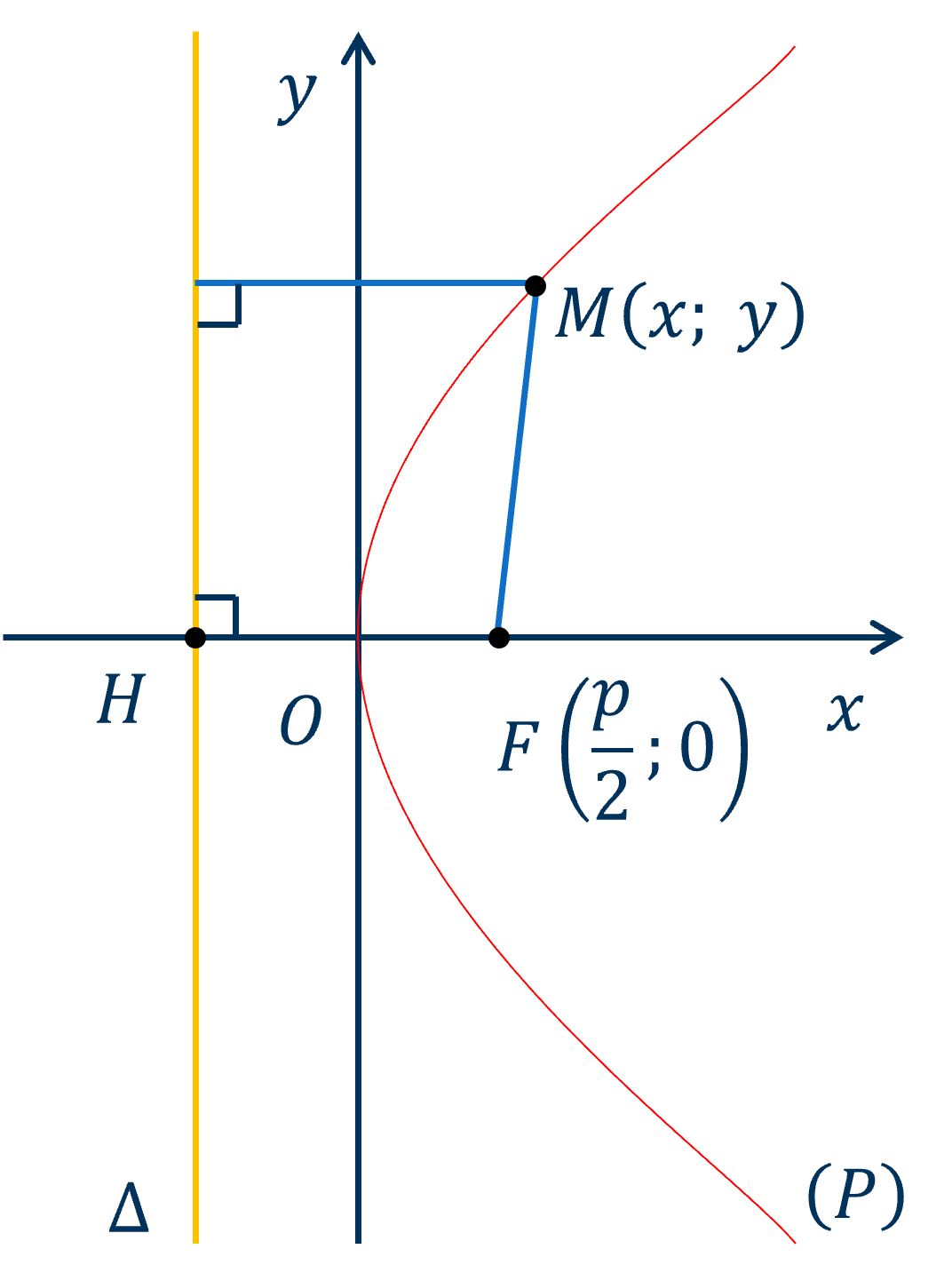
Điểm \(F\) được gọi là tiêu điểm, \(\Delta\) được gọi là đường chuẩn. Khoảng cách từ \(F\) đến \(\Delta\) được gọi là tham số tiêu của parabol đó.
Khi chọn hệ trục tọa độ như hình vẽ, phương trình chính tắc của đường parabol \(\left(P\right)\) là
\(y^2=2px\left(p>0\right)\).
\(F\left(\dfrac{p}{2};0\right)\) là tiêu điểm, \(x+\dfrac{p}{2}=0\) là phương trình đường chuẩn \(\Delta\).
Đây là bản xem trước câu hỏi trong video.
Hãy
đăng nhập
hoặc
đăng ký
và xác thực tài khoản để trải nghiệm học không giới hạn!
Câu 1 (1đ):
Với điểm F(0;1), điểm M(x;y). MF=
(x−0;y−1).
(0−x;1−y).
(x;y).
(x+0;y+1).
Câu 2 (1đ):
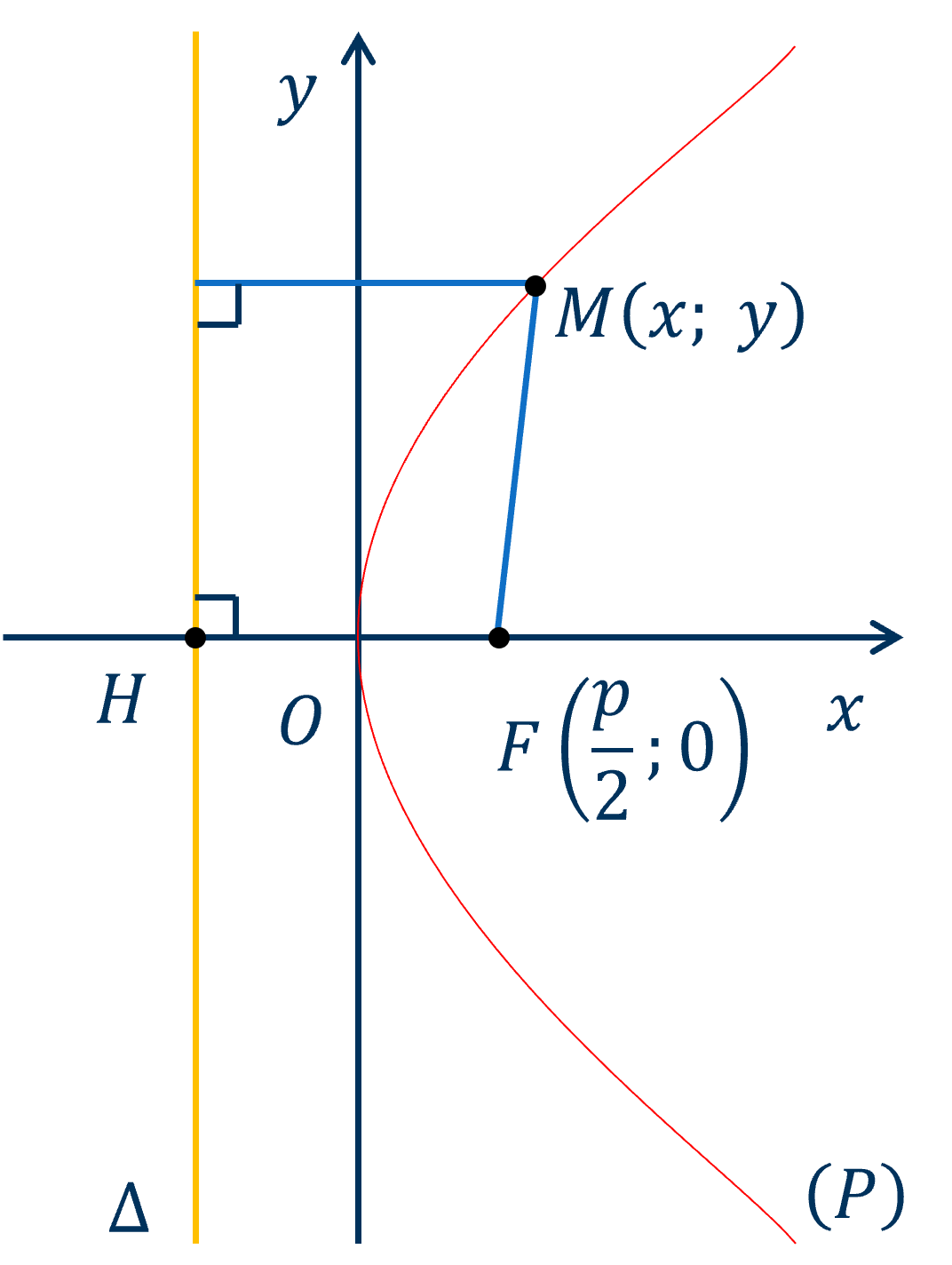
Phương trình đường thẳng Δ là
x−2p=0.
y−2p=0.
y+2p=0.
x+2p=0.
Câu 3 (1đ):
Parabol (P):y2=2x. Tiêu điểm F và đường chuẩn Δ của (P) là
F(2−1;0),Δ:x=21.
F(−1;0),Δ:x=1.
F(1;0),Δ:x=−1.
F(21;0),Δ:x=−21.
Văn bản dưới đây là được tạo ra tự động từ nhận diện giọng nói trong video nên có thể có lỗi
- phần cuối cùng là parabol Ta đi vào hoạt
- động 5
- cho protein
- xét điểm F có tọa độ 0 1 và đường thẳng
- delta y cùng 1 bằng 0 với điểm M bất kỳ
- ta cần chứng minh điểm M thuộc
- khoảng cách từ M thì Denta
- thầy có hình minh họa
- đầu tiên ta cần phải tính độ dài đoạn MF
- và khoảng cách từ M đến Delta theo x y
- đã
- có độ dài đoạn MF thì bằng độ dài của
- Vectơ MF
- bằng
- x trừ 0 bình phương không phải y - 1
- Bình Phương
- √
- = x² + Y - 1
- cắt tính khoảng cách từ M đến Delta ta
- áp dụng công thức tính khoảng cách từ
- một điểm đến một đường thẳng thì ta có
- được khoảng cách từ điểm M đến Delta
- trên tử là giá trị tuyệt đối khi ta thế
- tọa độ vào ta được giá trị của y + 1
- dưới mẫu là độ dài vectơ pháp tuyến của
- đoạn Delta
- căn của không mình + 1 Bình
- tiếp theo đó ta cho Ms bằng cách từ M
- đến Delta ta được
- căn của bình phương cộng với y - 1 bình
- phương bằng giá trị tuyệt đối của y + 1
- đến đây ta có thể bình phương hai vế và
- ta thu được x bình cộng với y - 1² = y +
- 1 bình phương bằng cách khai triển và
- thu gọn thì ta thu được x bình bằng 4y
- tương đương với y = 1/4 x bình y = 1/4x²
- chính là phương trình của Brom p
- vậy ta có điều phải chứng minh
- Ms bằng khoảng cách từ M đến Delta điểm
- M thuộc proton
- vậy propy y = 1/4 x bình là tập hợp
- những điểm cách đều điểm F có tọa độ 0;
- 1;0
- từ hoạt động này thì ta đã chia được
- định nghĩa hình học của một đường
- ta có định nghĩa
- cho một điểm F cố định là một đường
- thẳng delta cố định không đi qua f
- tập hợp các điểm M cách đều f và Delta
- được gọi là đường hay là
- parabols
- điều này gồm tập hợp các điểm M cách
- nhau
- Delta được gọi là đường chuẩn khoảng
- cách F đến Delta của là tham số tiêu của
- parabol đó
- ta đã có được định nghĩa hình học của
- một đường parabol Bây giờ ta sẽ đưa trục
- tọa độ vào đường này để tìm phương trình
- của đường pro đó
- set pro p với từng f và điều khiển Delta
- gọi p nhỏ là tham số tiêu của protein H
- là hình chiếu gốc của FC Delta ta chọn
- hệ trục tọa độ Oxy
- trùng với tia os
- và phương trình của Delta
- B ta cần giải thích vì sao để mở của
- prop khi và chỉ khi cảm thức sau đây đủ
- làm mát
- ta cần tìm tọa độ của điểm f và phương
- trình của Delta
- ta có P là tham số tiêu của propi bạn sẽ
- thành nghĩa hàm số tiêu sẽ là khoảng
- cách từ điểm F xuống đường thẳng delta
- Vậy là p đây chính bằng độ dài đoạn fh
- mà ta có được ô là trung điểm của hf do
- đó độ dài đoạn of
- tương tự tốc
- trừ p trên 2 không từ tọa độ điểm H ta
- sẽ tìm được phương trình của đoạn thẳng
- delta đường thẳng delta vuông góc với Ox
- nên có một Vector pháp tuyến để vectơ 1
- không
- sau đó nó có phương trình là 1 nhân với
- x trừ đi trừ p trên 2 là x cộng với y/2
- cộng với 0
- = 0 tương ứng với đều được x + X2 = 0
- định vị b
- để mở cuộc
- prof bằng khoảng cách từ M đến Delta
- vậy ta cần tính độ dài đoạn MF và khoảng
- cách từ M đến Delta
- làm tương tự như hoạt động vừa rồi
- độ dài đoạn MF = căn của X2 bình phương
- cộng với y bình phương
- khoảng cách mở Delta bằng giá trị của x
- bằng khoảng cách từ M đến Delta do đó ta
- sẽ được điều phải chứng minh căn của x
- bình phương cộng x bình phương sẽ bằng
- giá trị tuyệt đối của x + pi/2
- từ phương trình ta vừa thu được bằng sự
- biến đổi Bình Phương và thu gọn thì ta
- làm ở hoạt động 5 ta sẽ thu được phương
- trình của broad là y bình bằng 2tx
- ta có định nghĩa
- ta
- rồi hát thành Xuống góc của f Delta
- khi đó song hệ trục tọa độ Oxy với O là
- trung điểm của hf thì Ox trùng với tiêu
- srampion bằng 2 PX
- là phương trình này là phương trình 5
- thì phương trình 5 được gọi là phương
- trình chính tắc của
- protlat
- lớn hơn 0 là phương trình chính tắc của
- prolpt
- lưu ý là p phải lớn hơn 0
- Các em chú ý mối quan hệ hai chiều giữa
- đường prabul và phương trình của nó
- trong định nghĩa này ta có một số chú ý
- điều ích được gọi là trục đối xứng của
- propi
- cây nhỏ gọi là tham số tiêu của protein
- Và nếu điểm M có tọa độ xy thuộc
- x lớn bằng 0
- và điểm m' x - y cũng sẽ thuộc
- sau Ví dụ cho propi bình bằng 2x
- Tìm tưởng f và đường trở nên ta của
- propi B Tìm những điểm trên properat
- bằng 4 cho Bài này ý a ta cần tìm một số
- yếu tố cơ bản của parabol P là tiêu điểm
- và đường Trần ý b thì ta cần tìm điểm
- thuộc
- điều kiện ra trước
- cho mày này thỏa mãn điều kiện nó là
- khoảng cách từ f bằng 4
- Phương trình của protein bằng 2x do đó
- ta có là 2p = 2
- p1 là tham số tiêu của propi
- từ đây theo lý thuyết ta sẽ có được tọa
- độ của tuyển f và phương trình điều
- chỉnh Delta của
- props có tọa độ là 1/2 không và đồng
- chuẩn Delta là X = -1/2
- đến với B nếu ta đặt những điểm cần tìm
- là điểm M có tọa độ x0 y0
- bình phương bằng 2 0 bằng cách thế tốc
- độ vào propi
- và bài toán Yêu cầu là khoảng cách từ
- điểm đó tôi ép bằng 4 nên ta có là Ms
- mà do điểm M thuộc proton p đây là MF
- bằng khoảng cách m d Delta nên là khoảng
- cách từ M đến Delta cũng bằng 4 từ đây
- ta áp dụng công thức tính khoảng cách từ
- một điểm đến một đường thẳng ta thu được
- 4 bằng khoảng cách từ M để Delta bằng
- giá trị tuyệt đối của x0 + 1/2 và bằng
- x0 + 1/2 do x0 lớn bằng 0 vì x0 = 1/2
- lần y0 bình phương ta sẽ được phương
- trình này
- x0 = 4 - 1/2 bằng 7/2 Sau khi tìm được
- x0 ta cần tìm y0
- bằng căn 7 hoặc x0 = -7 vậy ta đã tìm
- được hai điểm thỏa mãn yêu cầu bài toán
- qua điểm có tọa độ 7,2
K
Khách
Bạn có thể đăng câu hỏi về bài học này ở đây
Chưa có câu hỏi thảo luận nào về bài giao này
OLMc◯2022
