olm
Đăng nhập Đăng ký Trợ giúp

Bài học cùng chủ đề

Báo cáo học liệu
Mua học liệu
Mua học liệu:
  • Số dư ví của bạn: 0 coin - 0 Xu
  • Nếu mua học liệu này bạn sẽ bị trừ: 2 coin\Xu
Thông tin của bạn

Ôn tập và kiểm tra cuối chương 9 SVIP

In bài

Yêu cầu đăng nhập!

Bạn chưa đăng nhập. Hãy đăng nhập để làm bài thi tại đây!

Câu 1 (1đ):

Khẳng định nào sau đây đúng?

Góc nội tiếp có số đo bằng một nửa số đo cung bị chắn.
Góc có đỉnh nằm trên đường tròn là góc nội tiếp đường tròn đó.
Góc có hai cạnh chứa các dây cung của đường tròn là góc nội tiếp đường tròn đó.
Góc nội tiếp có số đo bằng số đo cung bị chắn.
Câu 2 (1đ):

Cho tứ giác ABCDABCD nội tiếp một đường tròn có B^−D^=100∘\widehat{B}-\widehat{D} = 100^\circ. Khẳng định nào dưới đây đúng?

D^=40∘\widehat{D} = 40^\circ.
B^=40∘\widehat{B} = 40^\circ.
D^=100∘\widehat{D} = 100^\circ.
A^+C^=100∘\widehat{A}+\widehat{C} = 100^\circ.
Câu 3 (1đ):

Đa giác nào dưới đây không nội tiếp một đường tròn?

Hình chữ nhật.
Tam giác.
Đa giác đều.
Hình bình hành.
Câu 4 (1đ):

Cho tam giác vuông cân ABCABC có AB=AC=4AB = AC= 4 cm. Bán kính RR của đường tròn ngoại tiếp tam giác có độ dài là

22 cm.
2\sqrt{2} cm.
222\sqrt{2} cm.
424\sqrt{2} cm.
Câu 5 (1đ):

Cho tam giác đều ABCABC có đường cao AH=6AH = 6 cm. Bán kính rr của đường tròn nội tiếp tam giác có độ dài là

22 cm.
2\sqrt{2} cm.
3\sqrt{3} cm.
33 cm.
Câu 6 (1đ):

Nối đa giác đều với tên tương ứng của chúng.

Ngũ giác đều
Cửu giác đều
Lục giác đều
Thập giác đều
Bát giác đều
Đa giác đều 12 cạnh



Câu 7 (1đ):

Cho hình vuông ABCDABCD có OO là giao điểm của hai đường chéo. Phép quay tâm OO biến hình vuông ABCDABCD thành chính nó có góc quay là

90∘90^\circ.
210∘210^\circ.
45∘45^\circ.
135∘135^\circ.
Câu 8 (1đ):

Cho tam giác ABCABC nội tiếp đường tròn (O)(O). Gọi M,N,PM, N, P lần lượt là trung điểm của các cạnh BC,CA,ABBC, CA, AB. Khi đó:

⚡ Tứ giác ANOPANOP nội tiếp đường tròn đường kính .

⚡ Tứ giác nội tiếp đường tròn đường kính BOBO.

⚡ Tứ giác CMONCMON nội tiếp đường tròn bán kính :2 : 2.

Câu 9 (1đ):

Cho bát giác đều có tâm OO và ABAB là một cạnh, OHOH là đoạn vuông góc kẻ từ OO đến ABAB.

(Nhấp vào ô màu vàng để chọn đúng / sai)
a) AOB^=50∘ \widehat{AOB} = 50^\circ.
b) OH=OA.sin⁡45∘ OH = OA . \sin 45^\circ .
c) Phép quay 90∘90^\circ tâm OO biến bát giác đều thành chính nó.
d) AB=2OA.sin⁡22,5∘ AB = 2OA . \sin 22,5^\circ .
Câu 10 (1đ):

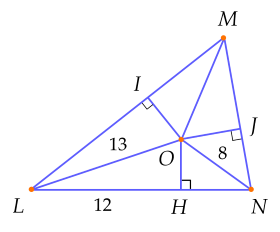
Một công viên hình tam giác được bao quanh bởi ba con đường ML,LN,NMML, LN, NM với kích thước (tính theo mét) được ghi trên bản vẽ trong hình (LO=13; LH=12; ON=8)(LO = 13; \, LH = 12; \, ON = 8). Người ta muốn dựng một trụ đèn tại một điểm cách đều ba con đường. Xác định khoảng cách từ điểm cần tìm đến ba con đường.

Trả lời:

OLM©2022OLM \copyright 2022
Truy vết IP log
Báo lỗi câu hỏi
Bạn đã gặp lỗi gì ở câu hỏi này, hãy mô tả vào ô bên dưới. Với mỗi lỗi thông báo đúng, OLM sẽ tặng bạn 1-3 ngày VIP!
Bạn có thể báo lỗi bằng hình ảnh tại đây!!!
Các khóa học có thể bạn quan tâm
Tổng thanh toán: 0đ (Tiết kiệm: 0đ)
Tới giỏ hàng
Yêu cầu VIP