Bài học cùng chủ đề
- Đại cương về đường thẳng và mặt phẳng
- Đại cương về đường thẳng và mặt phẳng (Tiếp)
- Giao tuyến của hai mặt phẳng
- Luyện tập
- Ôn tập: Tìm giao tuyến của hai mặt phẳng phân biệt
- Ôn tập: Tìm giao tuyến của hai mặt phẳng phân biệt
- Ôn tập: Tìm giao điểm của đường thẳng và mặt phẳng
- Ôn tập: Giao điểm của đường thẳng và mặt phẳng
- Ôn tập: Thiết diện
- Ôn tập: Thiết diện
- Phiếu bài tập: Đại cương về đường thẳng và mặt phẳng
Báo cáo học liệu
Mua học liệu
Mua học liệu:
-
Số dư ví của bạn: 0 coin - 0 Xu
-
Nếu mua học liệu này bạn sẽ bị trừ: 2 coin\Xu
Để nhận Coin\Xu, bạn có thể:

Ôn tập: Tìm giao tuyến của hai mặt phẳng phân biệt SVIP

Lưu ý: Ở điểm dừng, nếu không thấy nút nộp bài, bạn hãy kéo thanh trượt xuống dưới.
Bạn phải xem đến hết Video thì mới được lưu thời gian xem.
Để đảm bảo tốc độ truyền video, OLM lưu trữ video trên youtube. Do vậy phụ huynh tạm thời không chặn youtube để con có thể xem được bài giảng.
Nội dung này là Video có điểm dừng: Xem video kết hợp với trả lời câu hỏi.
Nếu câu hỏi nào bị trả lời sai, bạn sẽ phải trả lời lại dạng bài đó đến khi nào đúng mới qua được điểm dừng.
Bạn không được phép tua video qua một điểm dừng chưa hoàn thành.
Dữ liệu luyện tập chỉ được lưu khi bạn qua mỗi điểm dừng.
Cho hình chóp S.ABCD, đáy (ABCD) là tứ giác có các cặp cạnh đối không song song.

Điểm nào dưới đây là điểm chung của hai mặt phẳng (SAC) và (SBD)?
Cho hình chóp S.ABCD, đáy (ABCD) là tứ giác có các cặp cạnh đối không song song.
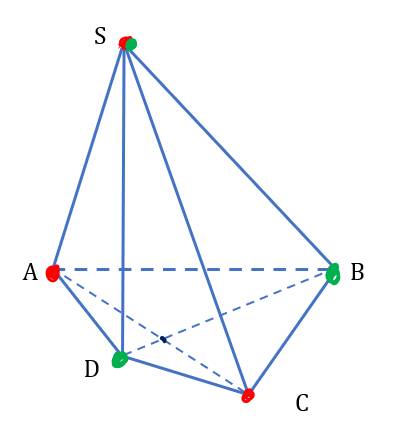
AC và BD
- không đồng phẳng.
- đồng phẳng.
Cho hình chóp (S.ABCD), đáy (ABCD) là tứ giác không có các cặp cạnh đối song song. (M) thuộc miền trong của tam giác (SCD).
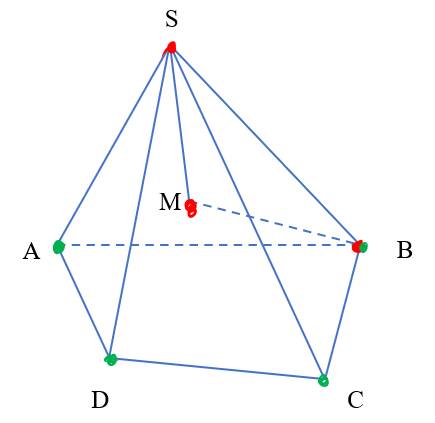
Điểm nào dưới đây là điểm chung của (SBM) và (ABCD)?
Cho hình chóp (S.ABCD), đáy (ABCD) là tứ giác không có các cặp cạnh đối song song. M thuộc miền trong của tam giác (SCD).

Đường thẳng nào sau đây nằm trong (ABCD) và đồng phẳng với SM?
Cho hình chóp (S.ABCD) , đáy (ABCD) là tứ giác có các cặp cạnh đối không song song. M nằm giữa S và A (M không trùng với S hoặc A). Tìm giao tuyến giữa (MCD) và (SBD).
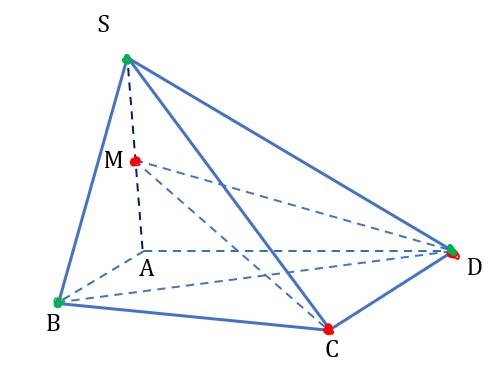
Điểm nào dưới đây là điểm chung của hai mặt phẳng (MCD) và (SBD)?
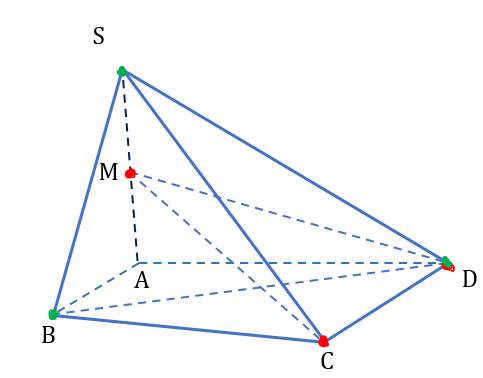
MC và SB là hai đường thẳng
- không đồng phẳng.
- đồng phẳng.
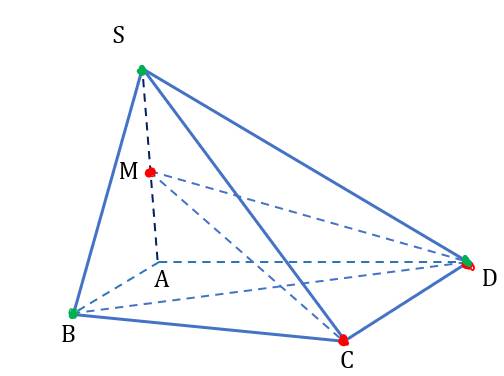
- (SBD)
- (ABCD)
- (SAC)

Trong (ABCD): AC∩BD=O.
=(SAC)∩(SBD)
Văn bản dưới đây là được tạo ra tự động từ nhận diện giọng nói trong video nên có thể có lỗi
- Xin chào em học sinh sau vường phép quay
- trở lại khoa toán trực tuyến cho biết
- bao nm Trong bài giảng này thầy sẽ mang
- đến cho cây một số dạng bài tập về quan
- hệ song sau A
- Ê mày đầu tiên đại cương về đường thẳng
- và mặt phẳng
- dạng thứ nhất xác định giao tuyến của
- hai mặt phẳng phân biệt p&q
- trước khi đi vào dạng một thì thấy có
- một số điều cần chú ý khi làm bài tập về
- quan hệ song song a
- ở đầu tiên là việc khoản vẽ hình
- Ừ thế em cần phải đảm bảo các thiết bị
- che khuất được vẽ bằng nét đứt
- anh em cần chuẩn bị bút bi thước kẻ bút
- chì và tẩy để vẽ hình
- Vì sao chúng ta cần chuẩn bị bút bi
- thước kẻ bút chì và tẩy
- Em gửi anh không gian thì chúng ta không
- thể tránh khỏi việc cần phải kéo ra để
- vẽ hình thế nên bút bi chúng ta sẽ vẽ
- những sự kiện mà để lại đã cho và chắc
- chắn không cần tẩy đi Còn bút chì chúng
- ta sẽ vẽ những nét chúng ta kéo dài để
- làm bài tập nhiều khi cách kéo dài của
- chúng ta chưa phù hợp thì chúng ta hoàn
- toàn có thể dùng tẩy để tẩy cái đó đi
- bác sĩ tẩy hết kéo ra thì những phần
- chúng ta vẽ bút bi thì sẽ không bị tẩy
- đi và không bị ảnh hưởng
- a tiếp theo là một số lưu ý khi học với
- tài sản trên oream kem nên dùng bài
- giảng để vẽ hình vào vở room nhá và hình
- của các em sẽ có điểm Nhìn giống với bài
- giảng thì cụ thể trong trận này và bài
- tập thể sẽ nó rõ hơn sau A
- a tiếp theo chúng ta sẽ sang phần lý
- thuyết về cách xác định giao tuyến của
- hai mặt phẳng phân biệt P và Q I
- ông Nguyễn Đình Minh họa thầy có hai mặt
- phẳng P và Q I
- so với mặt phẳng P là hình tam giác có
- một lâu mặt phẳng Q là hình tam giác có
- màu xanh lá cây như thế nào ạ
- Ừ để xác định giao tuyến giữa hai mặt
- phẳng thì bước đầu tiên chúng ta cần tìm
- hiểu chung đầu tiên
- một trong những dạng toán xác định giao
- tuyến của hai mặt phẳng phân biệt thì
- liệu trình đầu tiên thường rất dễ thấy
- ví dụ ở đây là điểm s
- Khi bữa thứ hai mình cần chọn ra một
- đường thẳng D nằm trong mặt phẳng P
- ngã ba đường thẳng d phẩy nằm trong mặt
- phẳng Q sao cho chúng đồng phẳng d đường
- thẳng D nằm trong mặt phẳng P D là đường
- thẳng d phẩy nằm trong mặt phẳng Q
- d b d phẩy đồng phẳng thì nên là có mặt
- phẳng r chứa đường thẳng d và d phải
- chúng ta tìm giao điểm giữa D và D phẩy
- thể đây đi vào đây phải cắt nhau tại i y
- vừa thủ Cường d phải từ y vừa chụp được
- màu xanh và y thuộc đường Lê Lợi thuộc
- đường màu nâu thì chứng tỏ Y sẽ thuộc
- vào hai mặt phẳng P và Q
- sau đó I là điểm Trung thứ hai và nối sy
- I
- tin tức là ta nối 2 điểm chung thì ta sẽ
- được giao tuyến của hai mặt phẳng P và Q
- I I
- khi chúng ta sang ví dụ đầu tiên
- số bài 1
- bài 1 yêu cầu chúng ta hình chóp SABCD
- Ừ để làm sao Cái đó b c d thì trước tiên
- chúng ta phải đẩy trước tại A B C D
- Cho đoạn thẳng AB thấy dự kiến có bị che
- khuất nên thầy sẽ lấy hết đất
- à Đây là hình chóp SABCD
- khi đến nơi thì anh dễ dùng bài giảm ạ
- và vẽ hình chóp SABCD với thứ tự điểm A
- B C D giữ nguyên như thế nào để chúng ta
- vào khung điểm Nghị ở hình chóp SABCD
- anh
- đi và yêu cầu chúng ta tìm giao tuyến da
- mặt phẳng SAC AA
- em hết
- a
- c e
- A
- và SBD s
- a b
- c d
- à à
- khi sex
- ý nghĩ đầu tiên của chúng ta để tìm giao
- tuyến giữa hai mặt phẳng là sẽ là xác
- điểm chồng động viên
- Ê tao thấy ngay điểm chung đầu tiên của
- hai mặt phẳng SAC và SBD là điểm s như
- vậy chúng ta đã xong bước đầu tiên tìm
- điểm chung thứ nhất
- Khi bữa tiếp theo chúng ta sẽ chọn một
- đường thẳng trong AC và một đường thẳng
- song SBD sao cho chúng đồng phẳng
- lý do s là điểm trưng đầu tiên nên chúng
- ta sẽ không chọn những đường thẳng đã có
- chứa điểm s nữa
- khi chúng ta còn lại hai đường thẳng đó
- là AC và BD thì chúng ta chọn
- Cho hai đường thẳng AC và BD của chúng
- ta là hai đường thẳng đồng phẳng
- bà cụ thể hơn chúng nằm trong mặt phẳng
- ABCD bằng trong mặt phẳng ABCD thì cho
- AC cắt BD tại O O
- Ừ
- nếu vậy ta thấy ngay cho thuộc vào đường
- thẳng ac
- ac lại nằm trong Excel nên o thuộc ac o
- thuộc SC
- ô ô thuộc vào BC và BD lại nằm trong SBD
- Thuộc gọi FPT ko thuộc SBD
- Ừ như vậy to vừa thuộc vừa dùng SBD nên
- O là điểm Trung thứ hai của Fac và SBD
- đốc tiếp theo chúng ta sẽ nổi s1o
- anh đào tạo Hoàng Anh fo là giao tuyến
- của hai mặt phẳng à
- a tiếp theo chúng ta xanh bài thứ hai
- Mở bài thứ hai cũng yêu cầu chúng ta vẫy
- hình chóp SABCD
- Ừ thì ta vẫn vẽ mặt phẳng đáy ABCD trước
- à à
- Ừ
- thế thì làm mờ thuộc miền trong của tam
- giác SCD Mở Đạt
- - 3 yêu cầu chúng ta tìm giao tuyến của
- 2 mặt phẳng sbm
- hai
- mặt phẳng s
- a b BM
- và mặt phẳng ABCD và mặt phẳng A
- AB C
- ở bước đầu tiên để tìm giao tuyến giữa
- hai mặt phẳng sbm và ABCD đó là chúng ta
- tìm điểm chung đầu tiên
- ừ ừ
- a b là điểm chung thứ nhất của hai mặt
- phẳng sbm và ABCD
- U60 tiếp theo chúng ta cần chọn ra một
- đường thẳng nằm trong mặt phẳng sbm vào
- một đường thẳng nằm xong mặt phẳng ABCD
- sao cho chúng đường khoảng
- mà cụ thể ở đây chúng ta sẽ không chọn
- những đường thẳng mà chứa điểm chung thứ
- nhất là điểm B nữa
- Ừ như vậy đối với mặt phẳng sbm chúng ta
- còn lại đường thẳng SM là dễ nhìn thấy
- con ở mặt phẳng ABCD chúng ta sẽ còn các
- đường thẳng không chứa điểm B đó là AC
- AD và đường thẳng C lên Ê
- anh ta thấy ngay đường thẳng SM của spm
- đồng phẳng với đường thẳng CD của mặt
- phẳng ABCD do chúng cùng nằm trong mặt
- phẳng sdc như vậy trong mặt phẳng SBC
- chúng ta sẽ cho SM cắt với BC tại K A
- ở thời K
- thủ tục SL ít
- e k thuộc SM Thế nên K cũng thuộc vào
- mặt phẳng s m b
- e k thuộc vào DC
- e k thuộc DC tiếng ca cũng thuộc mặt
- phẳng ABCD bằng xét có sau đó k là điểm
- Trung thứ hai của spm và ABCD nếu vậy
- giao tuyến của 2 mặt phẳng sbm và ABCD
- sẽ là KB
- nối BV k a
- khi chúng ta sang bài tiếp theo
- từ bài này Yêu cầu chúng ta vẫy hình
- chóp S.ABCD thì các em sẽ vẽ hình chóp
- SABCD giống ở trên bài giảng như sau
- ừ ừ
- chú ý cho làm mơ nằm giữa hết vào da
- khi mở không trùng với s và họa
- - 3 yêu cầu chúng ta tìm giao tuyến
- giữa mặt phẳng mcd
- i m c
- A và mặt phẳng SBD
- SB ê ê
- ở bước 1
- Chúng ta sẽ tìm điểm chung đầu tiên của
- hai mặt phẳng P
- a b điểm chung đầu tiên của hai mặt
- phẳng sang bước Thứ hai chúng ta sẽ cần
- chọn ra một đường thẳng tắm xong một CD
- và một đường thẳng nằm xong SBD sao cho
- chúng đồng đẳng điểm trung đầu tiên thì
- nên chúng ta sẽ không chọn những đường
- thẳng mà chứa điểm D
- khi chúng ta còn lại hai đường thẳng nó
- dễ nhìn thấy ở trên hình đó là MC
- t2b
- Cho hai đường thẳng MC và SB có đồng
- phẳng hay không
- khi MC
- tại SB
- do hai đường thẳng MC và SB không đồng
- phẳng thế nên chúng ta không thể cho MC
- cắt là SB và Tìm điểm chung thứ hai
- giống như hai bài trước đối với những
- dạng bài như thế này thì chúng ta sẽ làm
- như sau
- lý do MC và SB không đồng phẳng nên thấy
- sẽ không giữa đường thẳng SB ê
- anh nói tiếp sau đây thấy sẽ dựng một
- đường thẳng
- nằm trong SBD mà lại đồng phẳng với Mc
- Ừ để giữ một đường thẳng đồng phẳng với
- Mc thì trước hết chúng ta cần xem mc sẽ
- nằm trong mặt phẳng nào
- anh
- mơ xe của chúng ta nằm trong mặt phẳng
- SAC AA
- khi sex
- Vì sao mày bước Thứ hai chúng ta sẽ tìm
- giao tuyến
- giữa Fac và SBD
- chúng ta sẽ cần biết kết quả giao tuyến
- này là đường thẳng nào Thế gọi tạm là
- đường thẳng d Tại sao chúng ta phải xác
- định giao tuyến giữa Fac và SBD
- anh Bởi vì D chính là đường thẳng chúng
- ta cần trọ của mặt phẳng SBD mà nó đồng
- khoảng với Mc
- anh Bởi vì d thuộc ac = độ C cũng thuộc
- SC đến rõ ràng M C và D là hai đường
- thẳng đồng phẳng
- khi chúng ta lại cho nó khác nhau và
- khác nhau sẽ tìm một điểm chung thứ hai
- cụ thể ở đây chúng ta sẽ tìm giao tuyến
- giữa Fac và SBD
- A S A C E
- em hết
- a a
- c
- và SBD tìm giao tuyến của 2 mặt phẳng
- này chúng ta đã được làm được bài 1 rồi
- thì trong mặt phẳng ABCD ê ê
- khi
- các khóa AC cắt BD tại
- O O
- khi mà Dao Đỏ so
- có chứa giao tuyến của Fac và SBD ê
- em hẹn hò
- I là giao tuyến
- Ừ như vậy con sẽ ra đường thẳng chúng ta
- cần chọn ở trong mặt phẳng SBD ê
- anh em song với AC
- a cho xo cắt MC
- xo dao MC
- tại điểm k
- như vậy K Thuộc gọi to
- ý
- thì ca sẽ thuộc fpd-6s nằm trong sbt K
- thuộc và MC lên ca sẽ thuộc vào m CD do
- đó k là điểm Trung thứ hai của hai mặt
- phẳng mcd và SD ở
- ừ ừ
- ông bà nội đi với ca
- dao ngay
- a
- d k là giao tuyến của mcd và SBD
- ừ ừ
- số tk
- khi sinh ra tuyến tìm
- ừ ừ
- Ừ thế là chúng sanh phần trình bày ý
- có điều tiên đã có đây là điểm chung thứ
- nhất của mặt phẳng LCD và mặt phẳng SBD
- a tiếp theo thì chúng ta sẽ dựng giao
- tuyến của hai mặt phẳng SAC và SBD
- Ừ Thì trong mặt phẳng ABCD chúng ta sẽ
- cho AC cắt BD tại O O
- các axit cắt BD tại O
- bộ quà tặng những ai hết do chính là
- giao tuyến của AC và SD
- a tiếp theo chúng ta sẽ cho S O cắt để
- NC
- ở đại ca
- số báo danh tiếng ai K thuộc so o
- xe máy đo nằm xong SBD ilkay thuộc FPT
- anh cao tục ngồi c-mc nằm trong mcd nâng
- cao áp dụng LCD
- Chú Chó Đỏ K là điểm Trung thứ hai của
- hai mặt phẳng LCD và SBD
- cách chữa bệnh giao tuyển chúng ta cần
- tìm là đường thẳng dk dk
- vì
- vậy Thầy có cái nó đi xong dạng đầu tiên
- xác định giao tuyến của hai mặt phẳng
- phân biệt p&q chào các em à trước em học
- tốt
Bạn có thể đăng câu hỏi về bài học này ở đây
