Bài học cùng chủ đề
- Hai đường thẳng song song, chéo nhau
- Luyện tập
- Ôn tập: Giao tuyến của hai mặt phẳng chứa hai đường thẳng song song
- Ôn tập: Giao tuyến của hai mặt phẳng chứa hai đường thẳng song song
- Tham khảo: Một số kinh nghiệm khi làm toán dựng hình
- Ôn tập phần tham khảo: Một số kinh nghiệm khi làm toán dựng hình
- Phiếu bài tập: Hai đường thẳng song song, chéo nhau
Báo cáo học liệu
Mua học liệu
Mua học liệu:
-
Số dư ví của bạn: 0 coin - 0 Xu
-
Nếu mua học liệu này bạn sẽ bị trừ: 2 coin\Xu
Để nhận Coin\Xu, bạn có thể:
CHÚC MỪNG
Bạn đã nhận được sao học tập

Chú ý:
Thành tích của bạn sẽ được cập nhật trên bảng xếp hạng sau 1 giờ!
Tham khảo: Một số kinh nghiệm khi làm toán dựng hình SVIP

Nếu video không chạy trên Zalo, bạn vui lòng Click vào đây để xem hướng dẫn
Lưu ý: Ở điểm dừng, nếu không thấy nút nộp bài, bạn hãy kéo thanh trượt xuống dưới.
Bạn phải xem đến hết Video thì mới được lưu thời gian xem.
Để đảm bảo tốc độ truyền video, OLM lưu trữ video trên youtube. Do vậy phụ huynh tạm thời không chặn youtube để con có thể xem được bài giảng.
Nội dung này là Video có điểm dừng: Xem video kết hợp với trả lời câu hỏi.
Nếu câu hỏi nào bị trả lời sai, bạn sẽ phải trả lời lại dạng bài đó đến khi nào đúng mới qua được điểm dừng.
Bạn không được phép tua video qua một điểm dừng chưa hoàn thành.
Dữ liệu luyện tập chỉ được lưu khi bạn qua mỗi điểm dừng.
Lưu ý: Ở điểm dừng, nếu không thấy nút nộp bài, bạn hãy kéo thanh trượt xuống dưới.
Bạn phải xem đến hết Video thì mới được lưu thời gian xem.
Để đảm bảo tốc độ truyền video, OLM lưu trữ video trên youtube. Do vậy phụ huynh tạm thời không chặn youtube để con có thể xem được bài giảng.
Nội dung này là Video có điểm dừng: Xem video kết hợp với trả lời câu hỏi.
Nếu câu hỏi nào bị trả lời sai, bạn sẽ phải trả lời lại dạng bài đó đến khi nào đúng mới qua được điểm dừng.
Bạn không được phép tua video qua một điểm dừng chưa hoàn thành.
Dữ liệu luyện tập chỉ được lưu khi bạn qua mỗi điểm dừng.
Theo dõi OLM miễn phí trên Youtube và Facebook:
Đây là bản xem trước câu hỏi trong video.
Hãy
đăng nhập
hoặc
đăng ký
và xác thực tài khoản để trải nghiệm học không giới hạn!
Câu 1 (1đ):

Điểm nào dưới đây là điểm chung của hai mặt phẳng (SAM) và (SDC):
A.
S.
D.
M.
Câu 2 (1đ):
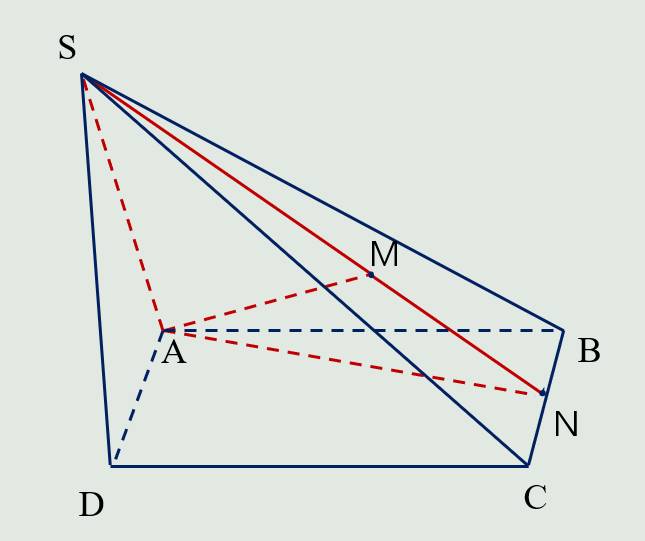
Đường thẳng nào sau đây của (SAM) đồng phẳng với đường thẳng DC của (SDC)?
SN.
AN.
AM.
SA.
Câu 3 (1đ):
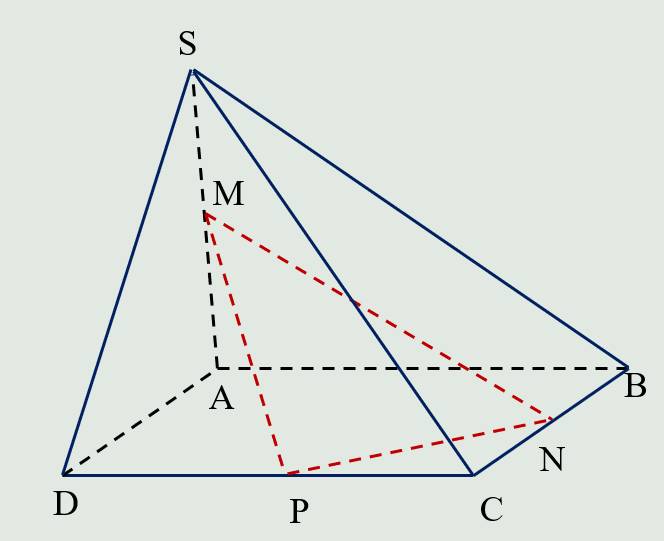
M là điểm chung của mặt phẳng (MNP) với những mặt phẳng nào dưới đây
(SAD).
(SDC).
(SAB).
(SBC).
(ABCD).
Câu 4 (1đ):
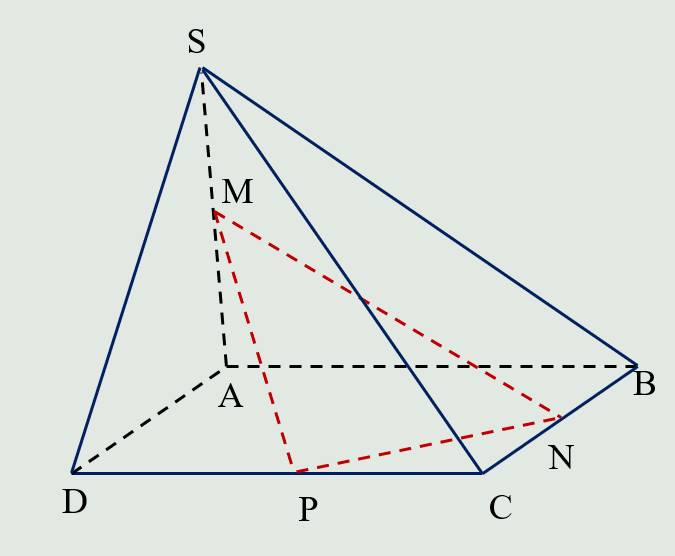
Đường thẳng PN đồng phẳng với đường thẳng nào của (SAB) ?
SA.
AB.
SB.
Câu 5 (1đ):
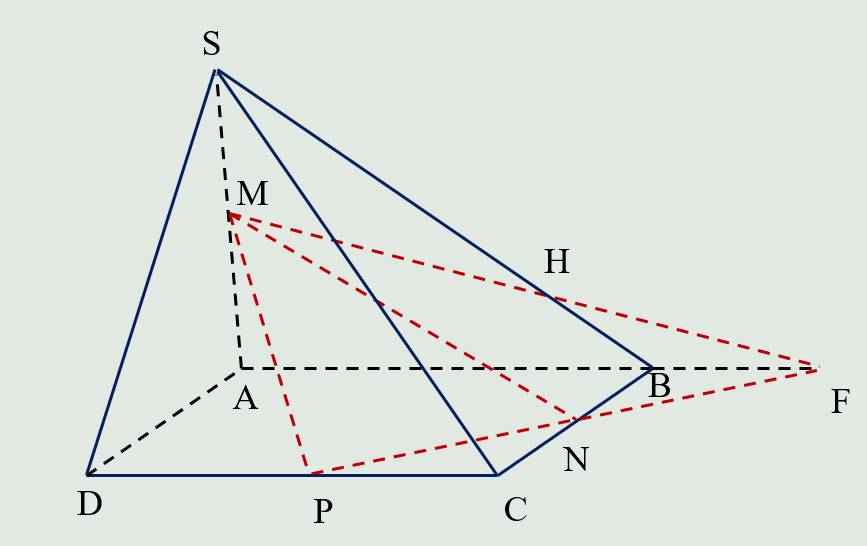
Đường thẳng PN đồng phẳng với đường thẳng nào của (SAD) ?
SD.
SA.
AD.
Văn bản dưới đây là được tạo ra tự động từ nhận diện giọng nói trong video nên có thể có lỗi
- Xin chào phê Ngọc Sơn
- Trong bài giảng lần này thể sẽ chia sẻ
- một số kinh nghiệm khi làm toàn sự hình
- không gian trong chương trình Toán lớp
- 11
- đầu tiên làm kỹ thuật mở rộng mặt phẳng
- ở trên bài giảng thầy có mặt phẳng a b c
- hình biểu diễn của mặt phẳng ABC là hình
- tam giác ABC
- biết mở rộng mặt phẳng chẳng qua là việc
- chúng ta mở rộng Tầm nhìn của mình đối
- với mặt phẳng ABC
- cụ thể hơn và chúng ta sẽ kéo dài đường
- thẳng AB về hai đầu hai kéo dài đường
- thẳng bc kéo dài đường thẳng ac thì tất
- cả những điểm thuộc đường thẳng AB AC
- hay là BC cũng đều thuộc mặt phẳng ABC
- tiếp theo những nước thể có một điểm M
- nằm ở miền trong tam giác ABC
- đường thẳng nối bvm cũng sẽ thuộc và mặt
- phẳng ABC
- hay là như thầy Nối A với M ở đây bị mờ
- thì em và cm cũng sẽ thuộc và mặt phẳng
- ABC
- như vậy việc mở rộng mặt phẳng sẽ khiến
- chúng ta có nhiều lựa chọn về đường
- thẳng trong mặt phẳng P hơn mặt phẳng P
- ở đây và mặt phẳng ABC ở trên hình với
- việc mở rộng mặt phẳng hay là kéo dài
- đường thẳng ta thấy áp dụng thường xuyên
- trong các bài toán tìm giao tuyến Hai
- các bài toán quy về tìm giao tuyến như
- là tìm giao điểm của đường thẳng với mặt
- phẳng Pantene thiết diện của hình chóp
- với mặt phẳng Tuy nhiên không phải bài
- toán dựng hình nào chúng ta cũng cố gắng
- kéo dài tất cả các đường thẳng có thể ra
- như thế rất là giỏi hình và cũng khó
- hình dung Và tiếp sau đây thời thế giới
- thiệu cho khai một số trường hợp mà
- chúng ta nên mở rộng mặt phẳng trước khi
- làm bài toán tìm giao tuyến hai phát bài
- toán quy về tìm giao tuyến
- ví dụ đầu tiên
- Cho hình chóp SABCD có đáy là hình bình
- hành
- M là điểm thuộc miền trong của tam giác
- SBC Mở ra
- đi và yêu cầu chúng ta tìm giao tuyến
- của Fa em anh vs DC
- đối với bài toán tìm giao tuyến của 2
- mặt phẳng thì sẽ có hai bức làm chính đó
- là tìm điểm chung thứ nhất và Bước tiếp
- theo là chọn ra hai đường thẳng đồng
- phẳng
- ở đây tiên tổng thống nhất thì chúng ta
- có điểm chung là điểm s
- p là điểm chung thứ nhất thì nên chúng
- ta sẽ không chọn những đường thẳng
- Ừ mà chửi ở trong hai mặt phẳng cụ thể
- hơn ở trong mặt phẳng SM chúng ta có
- đường thẳng a Mơ ở trong mặt phẳng SBC
- chúng ta có đường thẳng DC
- trên ta thấy An và DC là hai đường thẳng
- không đồng phẳng
- Chính vì thế đấy nước làm như bình
- thường thì chúng ta cần phải bỏ đi đường
- thẳng AM và cần dựng một đường thẳng nằm
- trong SM sao cho đồng phẳng với đường
- thẳng DC
- Tuy nhiên nếu như chúng ta áp dụng kỹ
- thuật mở rộng mặt phẳng trước khi chúng
- ta tìm giao tuyến thì có thể bước thứ 2
- của chúng ta sẽ được rút gọn đi khá là
- nhiều
- nhìn vào mặt phẳng m
- em y tá gợi ý mà khoảng cách m được biểu
- diễn bằng tam giác gồm 3 cạnh xa am và
- FM
- A và hơn nữa tao thấy mặt phẳng cách m
- cũng chưa chạm đến các phần điên tức là
- chạm đến các mặt phẳng tạo nên hình chóp
- sbcd
- Ừ thì chúng ta hoàn toàn có thể mở rộng
- mặt phẳng km
- bà cụ thể hơn chúng ta sẽ mở rộng mặt
- phẳng SM về hướng như thế nào
- về việc mở rộng mặt phẳng chẳng qua là
- kéo dài các đường thẳng
- ở dưới đây Chúng ta có 3 cạnh Sam và SM
- thì chúng ta sẽ kéo dài cạnh SM
- ở các đường thẳng bc tại điểm N
- A và Dao Đỏ
- Anh quay bị chúng ta tìm giao tuyến của
- mặt phẳng s AB với SC thì chúng ta sẽ có
- s l
- anh vs DC
- Ừ như vậy mà khoảng cái đam em sẽ được
- mở rộng thành mặt phẳng Bằng
- đến đây Chúng ta mở rộng mặt phẳng Sam
- thành mặt phẳng
- thì chúng ta sẽ có thêm 1 lựa chọn về
- đường thẳng của mặt phẳng nó sẽ đường
- thẳng n
- ở đây Al rõ ràng đồng phẳng với đường
- thẳng CD bởi vì chúng cũng nằm trong mặt
- phẳng ABCD
- ở đây chúng ta sẽ kéo dài l và c d
- sẽ cắt nhau tại E tính lại điểm Trung
- thứ hai của hai mặt phẳng
- A và AE sinh ra tuyến Cần tìm
- tự nhiên việc mở rộng mặt phẳng cũng sẽ
- phụ thuộc vào những mặt phẳng chúng ta
- đang xếp
- ở đây chúng ta đang xét mặt phẳng kết km
- thì nên chúng ta sẽ mở rộng theo chiều
- như thế nào chiều hướng xuống
- còn xanh ví dụ một phần và này yêu cầu
- chúng ta tìm giao tuyến giữa mặt phẳng
- ABM và mặt phẳng SCD
- a BM SCD
- nó đi ta thấy mà khoảng a BM hoàn toàn
- có thể mở rộng
- AE theo chiều như thế nào
- ở trong đoạn thẳng tạo bởi tam giác ABM
- chúng ta sẽ kéo dài cạnh BM
- sẽ cắt với đường thẳng SC đại ca
- chỉ có như vậy mặt phẳng AB ở chúng ta
- sẽ thành mặt phẳng apk
- vào đến nơi chúng ta mới tìm giao tuyến
- giữa mặt phẳng apk và mặt phẳng SBC
- máy bay tập này thì thấy dễ dàng cho cây
- làm xong Thần Bài tập
- sang đến kỹ thuật tiếp theo là về kinh
- nghiệm làm bài rất thiết diện đối với
- các bài toán tìm thiết diện thì chúng ta
- sẽ thường phải đối mặt với nhiều bài
- toán tìm giao tuyến như vậy Làm thế nào
- để chúng ta có thể tìm được ra bài toán
- nào làm bài toán dễ làm nhất
- thì sau phần là chúng ta sẽ nghiên cứu
- về vấn đề này đầu tiên thầy muốn nhắc
- lại ví dụ 2 ở trong bài giảng ôn tập cần
- thiết diện ví dụ 2 yêu cầu chúng ta phải
- hình chóp SABCD đáy là tứ giác có các
- cạnh đối không xong sao ah
- A M là điểm thuộc miền trong tam giác
- SCD tìm thiết diện của mob với hình chóp
- ở bài toán này để Dựng thiết diện của
- mặt phẳng bờ AB vẽ hình chóp SABCD thì
- chúng ta còn cần phải tìm giao tuyến
- Anh của mặt phẳng bờ AB với mặt phẳng
- SBD và mặt phẳng sau AB với mặt phẳng
- SBC và mặt phẳng trước
- Vàm AB và SCD là mặt phẳng bên phải này
- chúng ta sẽ đi qua từng bài toán tìm
- giao tuyến bài toán đầu tiên sẽ là bài
- toán tìm giao tuyến giữa bằng AB và mặt
- phẳng SBD
- em hẹn à ê ê
- Anh ta có ngay A điểm chung đầu tiên của
- hai mặt phẳng này
- ý nghĩa điểm trung đầu tiên thế nên ở
- bước thứ hai mặt phẳng bờ AB xếp còn lại
- đường thẳng BM và mặt phẳng SAD sẽ còn
- lại đường thẳng SD Tuy nhiên từ thẳng BM
- và đường thẳng SD là hai đường thẳng
- không đồng phẳng
- Vì thế nên chúng ta không thể cho hai
- đường thẳng này cắt nhau để tìm điểm
- chung thứ hai
- Vì sao lại còn thứ hai tìm giao tuyến
- của m a b với SBC
- SB BC
- Ừ thì tao thấy ngay bây giờ điểm chung
- đầu tiên
- do B điểm trung đầu tiên thì nên mặt
- phẳng mob sẽ còn lại đường thẳng AM là
- không chứa điểm B và mặt phẳng SBC sẽ
- còn lại đường thẳng SC là không chứa
- điểm B
- a-mei bằng FC
- từ đây ta không thấy m&a và SC cũng
- không phải là hai đường thẳng đồng phẳng
- và chúng ta cũng không thể cho chúng cắt
- nhau thì điểm Trung thứ hai và đến bài
- toán cuối cùng
- tìm giao tuyến giữa bằng AB và SCD
- tắt tiếng Anh mời điểm chung thứ nhất
- của hai mặt phẳng
- và ra mười là điểm chung đầu tiên thì
- lên mặt phẳng AB sẽ còn lại đường thẳng
- AB
- và đường thẳng AB đặt đồng phẳng và
- đường thẳng CD của mặt phẳng SCD
- lên bài toán tìm giao tuyến này chúng ta
- hoàn toàn thể cho a b cắt CD để tính
- điểm Trung thứ hai
- nếu bạn có điểm gì đặc biệt đối với 3
- bài toán tìm giao tuyến nay chúng ta đều
- thấy được Tìm điểm chung thứ nhất giữa 2
- mặt phẳng tiêu rất là dễ tìm sang đến
- bước thứ 2 chọn ra hai đường thẳng đồng
- phẳng Ừ thì rõ ràng mặt phẳng bờ AB phải
- gót ra một đường thẳng nằm trong nó
- cụ thể là BM macabê tương ứng với hình
- biểu diễn là ba cạnh của tam giác ABM
- hôm nay chúng ta để ý am và BM nằm ở vị
- trí khá là xấu bởi vì đoạn am và BM nằm
- lơ lửng ở trong hình chóp và không có
- mặt phẳng nào ngoài mặt phẳng ADM chứ am
- và BM cả
- còn lại đường thẳng AB thì nằm ở vị trí
- khá đẹp
- đứng thẳng AB phường nằm trong mặt phẳng
- đáy vừa làm xong mặt bên SAB của hình
- chóp như vậy rửa mặt phẳng AB chúng ta
- sẽ cố gắng giữ đường thẳng AB này cho
- tốt số 2 chọn ra hai đường thẳng đồng
- phẳng
- và do chúng ta giữ AB cho bớt số 2 thì m
- bắt buộc phải là điểm Trung thứ nhất anh
- mơ sẽ điểm chung thống nhất của bộ Abe
- và SCD
- như vậy chúng ta sẽ tìm giao tuyến giữa
- mặt phẳng bờ AB với mặt phẳng SCD trước
- cụ thể là chúng ta sẽ cho AB cắt CD
- Ừ tại điểm e e
- à à
- a tiếp theo chúng ta sẽ kết luận mới là
- giao tuyến của SD Maid
- và điện năng chúng ta sẽ lấy những phần
- thuộc Bình sót của cái dao từ nào ạ bà
- cụ thể hơn nó daika và đến nước chúng ta
- thấy ngay tiết diện sẽ là tứ giác aby ik
- Chúng ta thử áp dụng điều này
- vào ví dụ tiếp theo ví dụ 3
- Cho hình chóp s ABCD đáy ABCD là hình
- bình hành
- Gọi M là trung điểm AB A N là trung điểm
- bc P là trung điểm CD
- tìm thiết diện của hình chóp SABCD của
- mặt phẳng MNP ê
- ở đây để tìm thiết diện của hình chóp
- sbcd với mặt phẳng một nửa P
- Ừ thì chúng ta cần tìm giao tuyến của
- mặt phẳng MNP với các mặt của hình chóp
- cụ thể hơn ở đây là mặt phẳng đáy và bốn
- mặt bên
- người ta thấy nhanh giao tuyến giữa mặt
- phẳng MNP và ABCD là đường thẳng đường P
- ở đây thì chúng ta cần phải đối mặt với
- 4 bài toán tìm giao tuyến
- anh ta để biết được xem bài toán tìm
- giao tử nào là bài toán dễ làm hơn thì
- chúng ta cần phải nghiên cứu mặt phẳng
- MNP
- mặt phẳng MNP gọi trên hình đã được biểu
- diễn rồi tam giác MNP có 3 cạnh MP M N
- và p n e
- Ừ Thì trong ba phải này có hai cạnh đó
- là MP và M N là hai cạnh nằm ở vị trí
- không thuận lợi vì nó nằm lơ lượng ở
- trong hình chóp và không có mặt phẳng
- nào của hình chóp chứa đường thẳng MN
- hay là đường thẳng MP cả
- chúng ta sẽ giữ lại đường thẳng NP cho
- bước số 2 chọn ra hai đường thẳng đồng
- phẳng vì nó nằm ở vị trí thuận lợi và nó
- nằm trong mặt phẳng ABCD
- khi chúng ta cho đường thẳng NP cho bước
- thứ 2 thì chúng ta còn lại điểm m so với
- điểm Trung thứ nhất à
- Ừ chắc khỏe mờ là điểm chung thứ nhất
- của mặt phẳng MNP với mặt phẳng a b
- a&m quan điểm chung thứ nhất của mặt
- phẳng MNP với mặt phẳng SCD
- như vậy chúng ta sẽ làm hai bài toán tìm
- giao tuyến này trước thấy dễ làm với mặt
- phẳng SAB trước các thế nhanh m làm
- chung đầu tiên giữa hai mặt phẳng
- Anh bảo tiếp theo tìm em để sút đầu tiên
- thế nên mặt phẳng MNP sẽ còn lại đường
- thẳng pn ở trong nước hai đường thẳng
- đồng phẳng và rõ ràng BN đồng phẳng với
- đường thẳng AB của mặt phẳng SAB
- và trong mặt phẳng đáy thầy cho e b cắt
- pn
- tại điểm f
- và nối M với chúng ta sẽ có giao tuyến
- giữa mnp4 siyb
- có giao túi này rồi thì chúng ta sẽ giới
- hạn đó lại lấy những phần thuộc tính xót
- thôi
- vì thế gọi là đỉnh hát
- À thì ra tự giữ MNP và AV là MH
- từ tương tự Dự giao tuyến giữa M N P và
- s and M có điểm Trung thứ nhất có GM
- được trung đầu tiên thì nên chúng ta còn
- lại đường thẳng pn ở trong mặt phẳng MNP
- I TN2 đồng phẳng với đường thẳng Ad của
- mặt phẳng SCD Thế nên ta cho pn Với AD
- cắt nhau tại điểm E thì giao tuyến sẽ
- làm bờ e
- ở đây chúng ta cũng lấy những phần thuộc
- gia quyến nhưng mà cũng thuộc tỉnh shop
- tức là đoạn thẳng Mg đây là điểm của
- tao có thể thấy ngay giao tuyến của MNP
- với sdc SBC là GP
- còn giao tuyến của MNP và SBC là HN
- anh vào thiết diện của chúng ta là ngũ
- giác m
- h
- ntg3 này thì chúng ta thấy thiết diện là
- mình ngũ xác thì chúng ta lấy thằng Năm
- Giao tuyến của năm mặt phẳng của hình
- chóp với mặt cắt và không có sao thế nào
- Nằm hoàn toàn ở bên ngoài hình rõ cả tên
- chương trình bày thì các em chỉ cần nói
- ra cách dự và nêu ra các giao tuyến của
- mặt phẳng cách với từng mặt của hình
- chóp là sao cái có thể tham khảo trong
- bài giảng ôn tập phần thi diện
- như vậy về cái kinh nghiệm làm bài Dựng
- thiết diện mà thầy vừa nói cho các em
- thì nó chỉ khối khi chúng ta tìm thấy
- một đường thẳng nằm ở vị trí đêm tự là
- nó thuộc mặt phẳng của hình chóp ví dụ
- đây là đường thẳng b n thuộc BC D thì
- chúng ta sẽ giữ lại
- em còn đối với mày còn khó thì có thể
- mặt phẳng MNP sẽ không có đường thẳng
- nào nằm ở vị trí đẹp và đối với những
- bài toán thì tiết diện mà mặt phẳng cắt
- không có đường thẳng nào nằm ở vị trí
- thuận lợi
- đề thi chúng ta vẫn từ xây dựng giao
- tuyến giữa mặt phẳng cách với từng mặt
- của hình chóp như bình thường Tuy nhiên
- bài toán nào cũng sẽ khỏe như nhau cả và
- bài toán đó sẽ yêu cầu khi em phải có kỹ
- năng dựng hình và mở rộng mặt phẳng
- thông Phạm làm được các bạn như thế
- Mình chia sẻ kinh nghiệm của thời về bài
- toán dựng hình đến đây là hết cảm ơn các
- bạn đã lắng nghe
K
Khách
Bạn có thể đăng câu hỏi về bài học này ở đây
Chưa có câu hỏi thảo luận nào về bài giao này
OLMc◯2022
