Báo cáo học liệu
Mua học liệu
Mua học liệu:
-
Số dư ví của bạn: 0 coin - 0 Xu
-
Nếu mua học liệu này bạn sẽ bị trừ: 2 coin\Xu
Để nhận Coin\Xu, bạn có thể:

Một số bài tập về hình lăng trụ, hình hộp SVIP
Cho hình hộp ABCD.MNPQ. Gọi H là giao điểm của đường chéo BQ với (NCA). Tính tỉ số BQBH.
Cho các mệnh đề dưới đây:
(1): Mặt bên hình chóp cụt là những hình thang.
(2): Mặt bên hình lăng trụ là những hình bình hành.
(3): Hai đáy hình chóp cụt là những đa giác bằng nhau.
(4): Hình hộp là hình lăng trụ có mặt bên là những hình bình hành.
Số mệnh đề đúng là
Cho hình hộp ABCD.MNPQ. Gọi O,O′ lần lượt là tâm của ABNM và DCPQ. Khẳng định nào dưới đây sai?
Cho hình hộp chữ nhật ABCD.MNPQ. Gọi I là trung điểm của AB. Mặt phẳng (IMP) cắt hình hộp theo thiết diện là
Cho hình lăng trụ tam giác ABC.A1B1C1. Xác định giao tuyến của (BA1C1) và (B1AC).
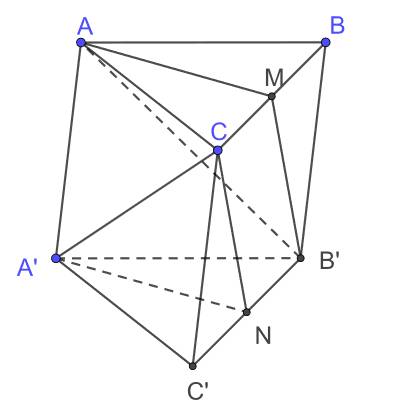
Cho hình lăng trụ tam giác ABC.A′B′C′. Gọi M là trung điểm BC, N là trung điểm B′C′ (tham khảo hình vẽ).
Kiểm tra tính đúng, sai của các khẳng định sau?
(Nhấp vào dòng để chọn đúng / sai)| (1) Đường thẳng MB′ song song với mặt phẳng (A′CN). |
|
| (2) A′N song song với mặt phẳng (AMB′). |
|
| (3) A′C cắt (AMB′) tại một điểm. |
|
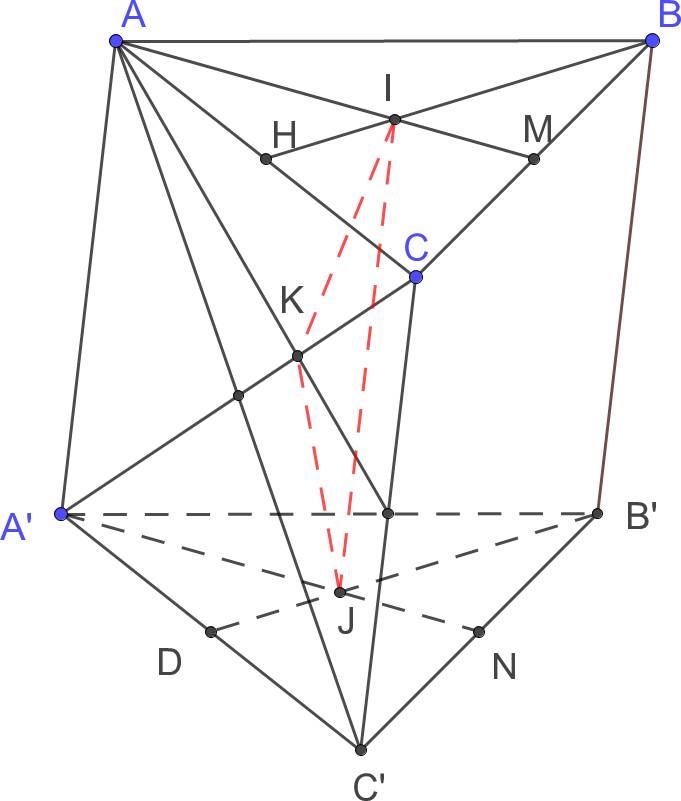
Cho lăng trụ tam giác ABC.A′B′C′. Gọi I,J,K lần lượt là trọng tâm △ABC, ΔA′B′C′,△ACC′. Gọi M,N,H lần lượt là trung điểm BC,B′C′,AC (tham khảo hình vẽ). Kiểm tra tính đúng, sai của các khẳng định sau?
(Nhấp vào dòng để chọn đúng / sai)| (1) Đường thẳng IJ song song với mặt phẳng (BB′C′C). |
|
| (2) Đường thẳng IK song song với đường thẳng BC′. |
|
| (3) Mặt phẳng (IJK) song song với mặt phẳng (BB′C′C). |
|
Cho hình lăng trụ ABC.A′B′C′ có đáy là tam giác đều cạnh a. Các mặt bên ABB′A′, ACC′A′ là hình vuông có tâm lần lượt là I và J. Gọi O là tâm đường tròn ngoại tiếp △ABC.
(Nhấp vào dòng để chọn đúng / sai)| Thiết diện của lăng trụ với mặt phẳng (IJO) là hình thang cân. |
|
| Đường thẳng IJ song song mặt phẳng (ABC). |
|
Cho hình chóp S.ABCD có đáy ABCD là hình bình hành tâm O. Gọi M,N lần lượt là trung điểm của SA và SD.
Xét tính đúng, sai của các khẳng định sau?
(Nhấp vào dòng để chọn đúng / sai)| (1) Đường thẳng MN song song với mặt phẳng (ABCD). |
|
| (2) Giao tuyến của hai mặt phẳng (OMN) và mặt phẳng (SBC) là đường thẳng đi qua O và song song với BC. |
|
| (3) Nếu P và Q lần lượt là trung điểm của AB và ON, thì PQ // (SBC). |
|
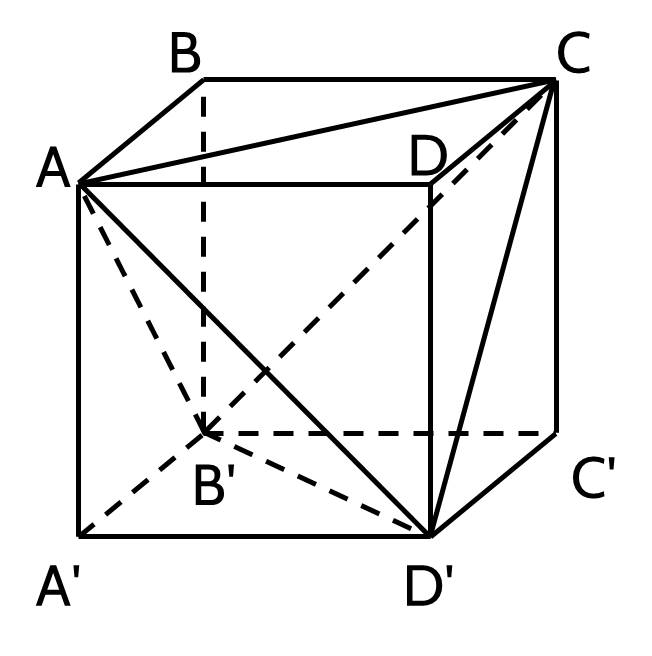
Cho hình lập phương ABCD.A′B′C′D′ cạnh a. Xét tứ diện AB′CD′. Cắt tứ diện đó bằng mặt phẳng đi qua tâm của hình lập phương và song song với mặt phẳng (ABC). Diện tích của thiết diện thu được là
(Tâm của hình lập phương là giao điểm của hai đường AC′ và A′C).

Bạn có thể đăng câu hỏi về bài học này ở đây
