Báo cáo học liệu
Mua học liệu
Mua học liệu:
-
Số dư ví của bạn: 0 coin - 0 Xu
-
Nếu mua học liệu này bạn sẽ bị trừ: 2 coin\Xu
Để nhận Coin\Xu, bạn có thể:

Dấu của nhị thức bậc nhất SVIP
1. Dấu của nhị thức bậc nhất
Định lý
Nhị thức bậc nhất $f(x) = ax+b$ ($a\ne 0$) có nghiệm \(x_0=-\dfrac{b}{a}\), $f(x)$ có giá trị:
+) cùng dấu với hệ số $a$ khi \(x\in\left(-\dfrac{b}{a};+\infty\right)\) hay \(x>x_0\);
+) cùng dấu với hệ số $a$ khi \(x\in\left(-\infty;-\dfrac{b}{a}\right)\) hay \(x< x_0\).
Bảng xét dấu
| $x$ | \(-\infty\) | \(-\dfrac{b}{a}\) | \(+\infty\) | ||
| $f(x) = ax+b$ | trái dấu với $a$ | $0$ | cùng dấu với $a$ |
Trục số
Nghiệm \(x_0=-\dfrac{b}{a}\) của nhị thức \(f\left(x\right)=ax+b\left(a\ne0\right)\) chia trục số thành hai khoảng.
Đồ thị
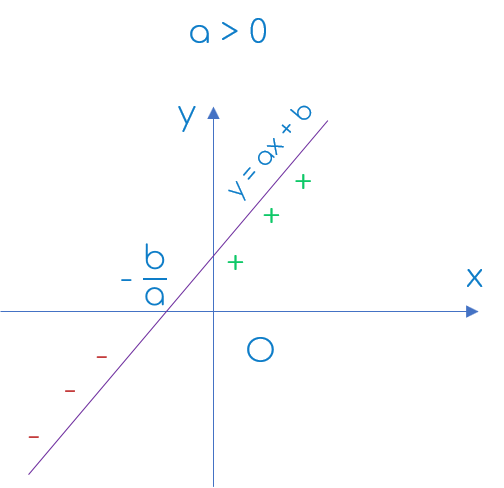 |
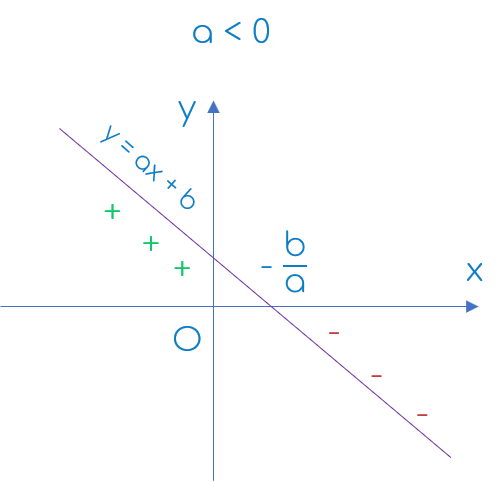 |
Ví dụ: Xét dấu nhị thức $g(x) = -2x + 4$.
$g(x)$ có nghiệm $x_0 = 2$ và có hệ số $a = -2 < 0$.
Bảng xét dấu:
| $x$ | \(-\infty\) | $2$ | \(+\infty\) | ||
| $g(x)$ | $+$ | $0$ | $-$ |
Dựa vào bảng xét dấu, kết luận: $g(x) < 0$ khi $x>2$; $g(x) > 0$ khi $x<2$.
2. Xét dấu tích thương các nhị thức bậc nhất
Xem video này để hiểu rõ hơn cách xét dấu biểu thức là tích thương các nhị thức bậc nhất.
Ví dụ: Xét dấu biểu thức \(f\left(x\right)=\dfrac{\left(4x-1\right)\left(x+2\right)}{-3x+5}\)
Giải:
$f(x)$ không xác định khi $x=\dfrac{5}{3}$.
Các nhị thức $4x - 1; x+2; -3x+5$ có các nghiệm lần lượt là \(\dfrac{1}{4};-2;\dfrac{5}{3}\). Các nghiệm này chia khoảng \(\left(-\infty;+\infty\right)\) thành bốn khoảng, trong mỗi khoảng các nhị thức đang xét có dấu hoàn toàn xác định.
| $x$ | $-\infty$ | $-2$ | $\dfrac{1}{4}$ | $\dfrac{5}{3}$ | $+\infty$ | |||||||
| $4x-1$ | $-$ | $-$ | $0$ | $+$ | $+$ | |||||||
| $x+2$ | $-$ | $0$ | $+$ | $+$ | $+$ | |||||||
| $-3x+5$ | $+$ | $+$ | $+$ | $0$ | $-$ | |||||||
| $f(x)$ | $+$ | $0$ | $-$ | $0$ | $+$ | $||$ | $-$ | |||||
Từ bảng xét dấu ta thấy:
$f(x) > 0$ khi $x \in (-\infty;-2)$ hoặc \(x\in\left(\dfrac{1}{4};\dfrac{5}{3}\right)\); $f(x) < 0$ khi \(x\in\left(-2;-\dfrac{1}{4}\right)\) hoặc \(x\in\left(\dfrac{5}{3};+\infty\right)\);
$f(x) = 0$ khi \(x=-2\) hoặc \(x=\dfrac{1}{4}\); $f(x)$ không xác định khi \(x=\dfrac{5}{3}\) (kí hiệu bởi || trong bảng).
3. Áp dụng vào giải bất phương trình
Bất phương trình tích/ chứa ẩn ở mẫu thức
Ví dụ: Giải bất phương trình \(\dfrac{1}{1-x}\ge1\quad\left(1\right)\).
Giải: Ta biến đổi bất phương trình ban đầu về dạng \(f\left(x\right)\ge0\), sau đó xét dấu biểu thức $f(x)$ để tìm ra khoảng mà $f(x)$ mang dấu dương hoặc bằng $0$.
\(\left(1\right)\Leftrightarrow\dfrac{1}{1-x}\ge1\Leftrightarrow\dfrac{1}{1-x}-1\ge0\Leftrightarrow\dfrac{x}{1-x}\ge0.\)
Xét dấu biểu thức \(f\left(x\right)=\dfrac{x}{1-x}\) ta suy ra nghiệm của bất phương trình $(1)$ là \(0\le x< 1\).
Bất phương trình chứa ẩn trong dấu giá trị tuyệt đối
Ví dụ: Giải bất phương trình \(\left|x-1\right|\le2\left|-x-4\right|+x-2\)
Giải: Khử dấu giá trị tuyệt đối
Xem video này để hiểu rõ hơn cách xét lập bảng khử dấu giá trị tuyệt đối.
| $x$ | $-\infty$ | $-4$ | $1$ | $+\infty$ | |||||
| $|x-1|$ | $-(x-1)$ | $-(x-1)$ | $0$ | $x-1$ | |||||
| $2|-x-4|$ | $2(-x-4)$ | $0$ | $-2(-x-4)$ | $-2(x-4)$ | |||||
Dựa vào bảng trên ta có
a) với $x \le -4$, bất phương trình thành
\(-x+1\le-2x-7+x-2\) hay \(1\le-10\),
do đó trong khoảng \(\left(-\infty;-4\right]\), bất phương trình vô nghiệm.
b) Với \(-4< x\le1\), bất phương trình trở thành
\(-x+1\le2x+8+x-2\)
\(\Leftrightarrow4x\ge-5\Leftrightarrow x\ge-\dfrac{5}{4}.\)
Do đó, trong khoảng \(\left(-4;1\right]\) phương trình có nghiệm \(-\dfrac{5}{4}\le x\le1\).
c) với $x>1$, bất phương trình trở thành
\(x-1\le2x+8+x-2\)
\(\Leftrightarrow2x\ge-7\Leftrightarrow x\ge-\dfrac{5}{2}.\)
Vậy mọi $x>1$ đều là nghiệm của bất phương trình.
Tổng hợp các kết quả ta được nghiệm của bất phương trình đã cho là
\(\left\{{}\begin{matrix}-\dfrac{5}{4}\le x\le1\\x>1\end{matrix}\right.\) hay \(x\ge-\dfrac{5}{4}.\)
Bạn có thể đăng câu hỏi về bài học này ở đây
