Bài học cùng chủ đề
- Phương trình đường thẳng. Vị trí tương đối giữa hai đường thẳng. Góc và khoảng cách
- Phương trình tổng quát của đường thẳng
- Phương trình tham số của đường thẳng
- Vị trí tương đối giữa hai đường thẳng
- Góc giữa hai đường thẳng
- Khoảng cách từ một điểm đến một đường thẳng
- Vectơ chỉ phương và vectơ pháp tuyến của đường thẳng
- Phương trình tham số của đường thẳng
- Phương trình tổng quát của đường thẳng (phần 1)
- Phương trình tổng quát của đường thẳng (phần 2)
- Vị trí tương đối giữa hai đường thẳng (Phần 1)
- Vị trí tương đối giữa hai đường thẳng (Phần 2)
- Góc giữa hai đường thẳng
- Khoảng cách (phần 1)
- Khoảng cách (phần 2)
- Luyện tập tổng hợp
Báo cáo học liệu
Mua học liệu
Mua học liệu:
-
Số dư ví của bạn: 0 coin - 0 Xu
-
Nếu mua học liệu này bạn sẽ bị trừ: 2 coin\Xu
Để nhận Coin\Xu, bạn có thể:

Phương trình đường thẳng. Vị trí tương đối giữa hai đường thẳng. Góc và khoảng cách SVIP
1. Phương trình đường thẳng
Vectơ chỉ phương và vectơ pháp tuyến của đường thẳng
Vectơ \(\overrightarrow{u}\) được gọi là vectơ chỉ phương của đường thẳng \(\Delta\) nếu \(\overrightarrow{u}\ne\overrightarrow{0}\) và giá của \(\overrightarrow{u}\) song song hoặc trùng với \(\Delta\).
Vectơ \(\overrightarrow{n}\) được gọi là vectơ pháp tuyến của đường thẳng \(\Delta\) nếu \(\overrightarrow{n}\ne\overrightarrow{0}\) và \(\overrightarrow{n}\) vuông góc với vectơ chỉ phương của \(\Delta\).
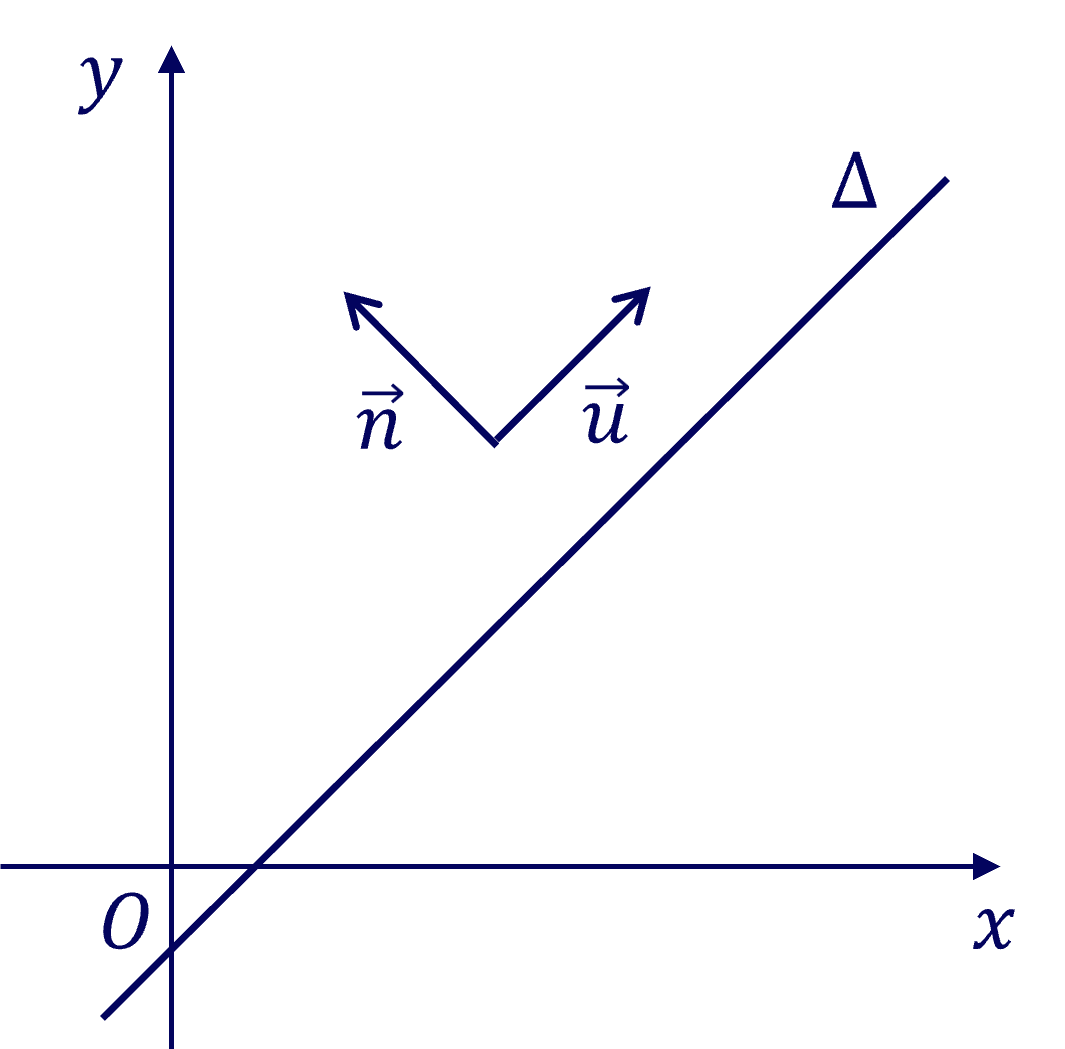
Chú ý:
- Nếu đường thẳng \(\Delta\) có vectơ pháp tuyến \(\overrightarrow{n}=\left(a;b\right)\) thì \(\Delta\) sẽ nhận \(\overrightarrow{u}=\left(b;-a\right)\) hoặc \(\overrightarrow{u}=\left(-b;a\right)\) là một vectơ chỉ phương.
- Nếu \(\overrightarrow{u}\) là vectơ chỉ phương của đường thẳng \(\Delta\) thì \(k\overrightarrow{u}\) (\(k\ne0\)) cũng là vectơ chỉ phương của \(\Delta\).
- Nếu \(\overrightarrow{n}\) là vectơ pháp tuyến của đường thẳng \(\Delta\) thì \(k\overrightarrow{n}\) (\(k\ne0\)) cũng là vectơ pháp tuyến của \(\Delta\).
Phương trình tham số của đường thẳng
Trong mặt phẳng \(Oxy\), ta gọi: \(\left\{{}\begin{matrix}x=x_0+tu_1\\y=y_0+tu_2\end{matrix}\right.\) (với \(u_1^2+u_2^2>0,t\inℝ\)) là phương trình tham số của đường thẳng \(\Delta\) đi qua điểm \(M_0\left(x_0;y_0\right)\) có vectơ chỉ phương \(\overrightarrow{u}=\left(u_1;u_2\right)\).
Chú ý: Cho \(t\) một giá trị cụ thể thì ta xác định được một điểm trên đường thẳng \(\Delta\) và ngược lại.
Phương trình tổng quát của đường thẳng
Trong mặt phẳng \(Oxy\), mỗi đường thẳng đều có phương trình tổng quát dạng
\(ax+by+c=0\),
với \(a\) và \(b\) không đồng thời bằng \(0\).
Chú ý:
- Mỗi phương trình \(ax+by+c=0\) (\(a\) và \(b\) không đồng thời bằng \(0\)) đều xác định một đường thẳng có vectơ pháp tuyến \(\overrightarrow{n}=\left(a;b\right)\).
- Khi cho phương trình đường thẳng \(ax+by+c=0\), ta hiểu \(a\) và \(b\) không đồng thời bằng \(0\).
Ví dụ: Trong mặt phẳng \(Oxy\), cho điểm \(A\left(2;3\right)\) và hai vectơ \(\overrightarrow{u}=\left(1;2\right)\), \(\overrightarrow{n}=\left(-2;1\right)\).
a) Lập phương trình tổng quát của đường thẳng \(A\) và nhận \(\overrightarrow{n}\) là vectơ pháp tuyến.
b) Lập phương trình tham số của đường thẳng đi qua \(A\) và nhận \(\overrightarrow{u}\) là vectơ chỉ phương.
c) Lập phương trình tổng quát và phương trình tham số của đường thẳng đi qua điểm \(A\) và điểm \(B\left(3;2\right)\).
Giải:
a) Phương trình tổng quát của đường thẳng cần tìm là
\(-2\left(x-2\right)+1\left(y-3\right)=0\Leftrightarrow-2x+y+1=0\).
b) Phương trình tham số của đường thẳng cần tìm là
\(\left\{{}\begin{matrix}x=2+t\\y=3+2t.\end{matrix}\right.\)
c) Đường thẳng \(AB\) nhận \(\overrightarrow{AB}\) là một vectơ chỉ phương.
\(\overrightarrow{AB}=\left(3-2;2-3\right)=\left(1;-1\right)\).
Phương trình tham số của đường thẳng \(AB\) là
\(\left\{{}\begin{matrix}x=2+t\\y=3-t.\end{matrix}\right.\)
Do \(\overrightarrow{AB}=\left(1;-1\right)\) là một vectơ chỉ phương của đường thẳng \(AB\) nên \(\overrightarrow{n_{AB}}=\left(1;1\right)\) là một vectơ pháp tuyến của đường thẳng \(AB\).
Phương trình tổng quát của đường thẳng \(AB\) là
\(1\left(x-2\right)+1\left(y-3\right)=0\Leftrightarrow x+y-5=0\).
2. Vị trí tương đối của hai đường thẳng
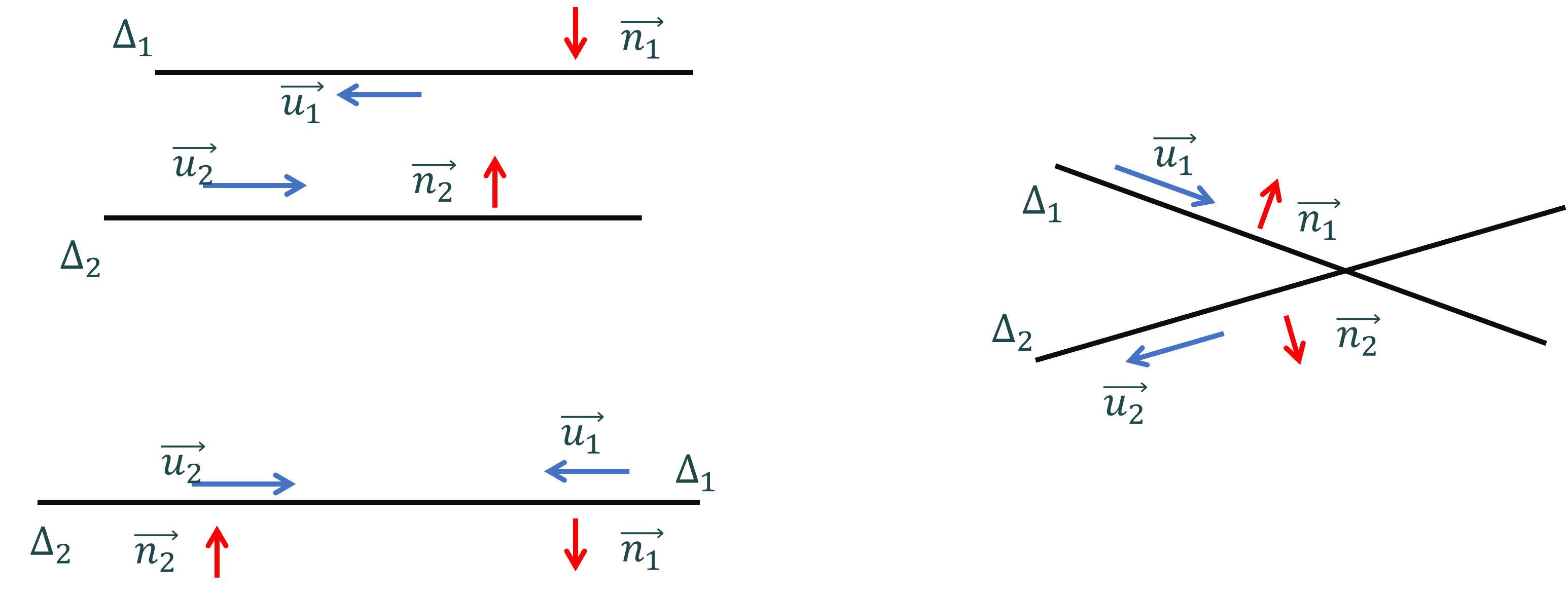
Nếu \(\overrightarrow{n_1}\) và \(\overrightarrow{n_2}\) cùng phương thì \(\Delta_1\) và \(\Delta_2\) song song hoặc trùng nhau. Lấy một điểm \(P\) tùy ý trên \(\Delta_1\).
- Nếu \(P\in\Delta_2\) thì \(\Delta_1\equiv\Delta_2\).
- Nếu \(P\notin\Delta_2\) thì \(\Delta_1//\Delta_2\).
Nếu \(\overrightarrow{n_1}\) và \(\overrightarrow{n_2}\) không cùng phương thì \(\Delta_1\) và \(\Delta_2\) cắt nhau tại một điểm \(M\left(x_0;y_0\right)\) với \(\left(x_0;y_0\right)\) là nghiệm của hệ phương trình:
\(\left\{{}\begin{matrix}a_1x+b_1y+c_1=0\\a_2x+b_2y+c_2=0.\end{matrix}\right.\)
Chú ý:
- Nếu \(\overrightarrow{n_1}.\overrightarrow{n_2}=0\) thì \(\overrightarrow{n_1}\perp\overrightarrow{n_2}\), suy ra \(\Delta_1\perp\Delta_2\).
- Để xét hai vectơ \(\overrightarrow{n_1}\left(a_1;b_1\right)\) và \(\overrightarrow{n_2}\left(a_2;b_2\right)\) cùng phương hay không cùng phương, ta xét biểu thức \(a_1b_2-a_2b_1\):
- Nếu \(a_1b_2-a_2b_1=0\) thì hai vectơ cùng phương.
- Nếu \(a_1b_2-a_2b_1\ne0\) thì hai vectơ không cùng phương.
Trong trường hợp tất cả các hệ số \(a_1\), \(a_2\), \(b_1\), \(b_2\) đều khác \(0\), ta có thể xét hai trường hợp:
- Nếu \(\dfrac{a_1}{a_2}=\dfrac{b_1}{b_2}\) thì hai vectơ cùng phương.
- Nếu \(\dfrac{a_1}{a_2}\ne\dfrac{b_1}{b_2}\) thì hai vectơ không cùng phương.
Ví dụ: Cho đường thẳng \(d\) có phương trình \(2x-y+1=0\). Xét vị trí tương đối của \(d\) với mỗi đường thẳng sau:
a) \(\Delta_1:\left\{{}\begin{matrix}x=1+t\\y=-1+2t.\end{matrix}\right.\)
b) \(\Delta_2:y=x+2\).
c) \(\Delta_3:\dfrac{x}{4}-\dfrac{y}{8}=-\dfrac{1}{8}\).
Giải:
a) \(\Delta_1:\left\{{}\begin{matrix}x=1+t\\y=-1+2t\end{matrix}\right.\) nên có một vectơ chỉ phương là \(\overrightarrow{u_{\Delta_1}}=\left(1;2\right)\) suy ra một vectơ pháp tuyến của đường thẳng này là \(\overrightarrow{n_{\Delta_1}}=\left(2;-1\right)\).
Ta lấy \(t=0\), ta được điểm \(M\left(1;-1\right)\in\Delta_1\).
Phương trình tổng quát của đường thẳng \(\Delta_1\) là \(2x-y-3=0\).
Hai đường thẳng \(d\) và \(\Delta_1\) có hai vectơ pháp tuyến là \(\overrightarrow{n_d}=\left(2;-1\right)\) và \(\overrightarrow{n_{\Delta_1}}=\left(2;-1\right)\) cùng phương nên \(d\) và \(\Delta_1\) song song hoặc trùng nhau.
Mà ta có \(M\left(1;-1\right)\) thuộc đường thẳng \(\Delta_1\) nhưng không thuộc đường thẳng \(d\) vì \(2.1-\left(-1\right)+1=4\ne0\).
Do đó hai đường thẳng này song song với nhau.
b) Đường thẳng \(\Delta_2\) có phương trình \(y=x+2\Leftrightarrow x-y+2=0\) nên có vectơ pháp tuyến \(\overrightarrow{n_{\Delta_2}}=\left(1;-1\right)\).
Ta có \(\dfrac{2}{1}\ne\dfrac{-1}{-1}\), do đó hai vectơ pháp tuyến của hai đường thẳng \(d\) và \(\Delta_2\) không cùng phương. Suy ra hai đường thẳng \(d\) và \(\Delta_2\) cắt nhau.
c) Đường thẳng \(\Delta_3\) có phương trình \(\dfrac{x}{4}-\dfrac{y}{8}=-\dfrac{1}{8}\Leftrightarrow2x-y+1=0\).
Vậy hai đường thẳng \(d\) và \(\Delta_3\) là một, hay chúng trùng nhau.
3. Góc giữa hai đường thẳng
Khái niệm góc giữa hai đường thẳng
Hai đường thẳng \(\Delta_1\) và \(\Delta_2\) cắt nhau tạo thành bốn góc. 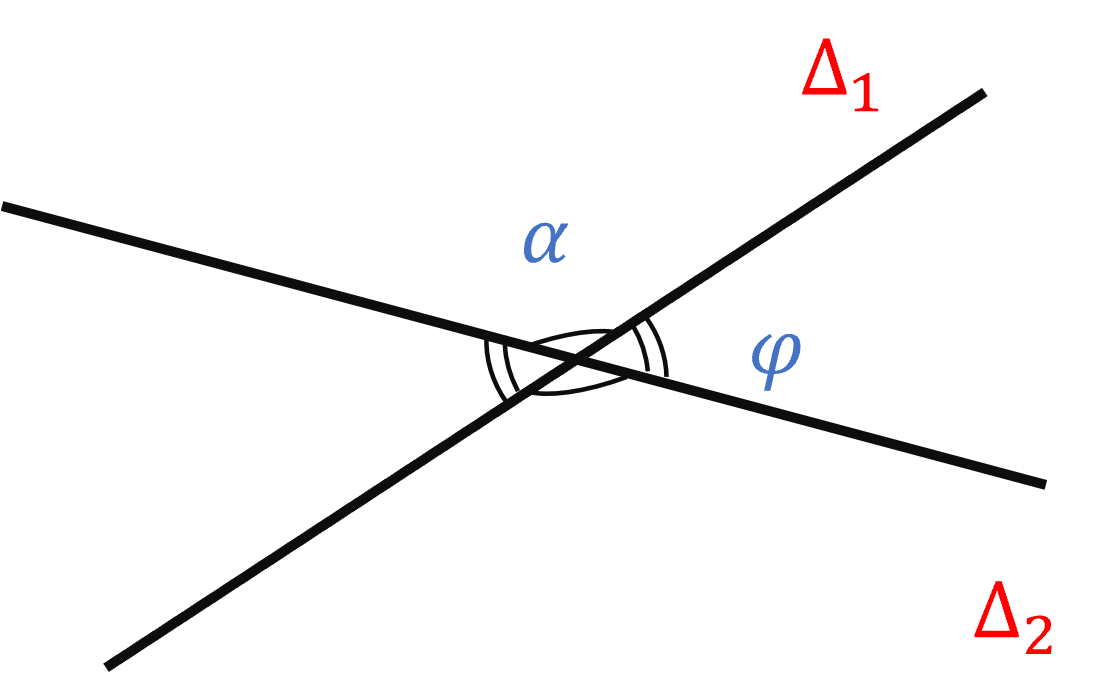
- Nếu \(\Delta_1\) không vuông góc với \(\Delta_2\) thì góc nhọn trong bốn góc đó được gọi là góc giữa hai đường thẳng \(\Delta_1\) và \(\Delta_2\).
- Nếu \(\Delta_1\) vuông góc với \(\Delta_2\) thì ta nói góc giữa \(\Delta_1\) và \(\Delta_2\) bằng \(90^o\).
Công thức tính góc giữa hai đường thẳng
Cho hai đường thẳng \(\Delta_1:a_1x+b_1y+c_1=0\) (\(a_1^2+b_1^2>0\)), \(\Delta_2:a_2x+b_2y+c_2=0\) (\(a_2^2+b_2^2>0\)) có vectơ pháp tuyến lần lượt là \(\overrightarrow{n_1}\) và \(\overrightarrow{n_2}\).
Ta có công thức: \(\cos\left(\Delta_1,\Delta_2\right)=\dfrac{\left|a_1a_2+b_1b_2\right|}{\sqrt{a_1^2+b_1^2}.\sqrt{a_2^2+b_2^2}}\).
Chú ý:
- Nếu \(\Delta_1\) và \(\Delta_2\) lần lượt có phương trình \(a_1x+b_1y+c_1=0\) và \(a_2x+b_2y+c_2=0\) thì ta có: \(\left(\Delta_1,\Delta_2\right)=90^o\Leftrightarrow a_1a_2+b_1b_2=0\).
- Nếu \(\Delta_1\) và \(\Delta_2\) lần lượt có phương trình \(y=k_1x+m_1\) và \(y=k_2x+m_2\) thì ta có: \(\left(\Delta_1,\Delta_2\right)=90^o\Leftrightarrow k_1k_2=-1\).
Ví dụ: Tính góc giữa các cặp đường thẳng sau:
a) \(d_1:\sqrt{3}x-y-4=0\) và \(d_2:x-\sqrt{3}y+2=0;\)
b) \(d_3:\left\{{}\begin{matrix}x=2+3t\\y=1+t\end{matrix}\right.\) và \(d_4:\left\{{}\begin{matrix}x=1+4t'\\y=5-2t';\end{matrix}\right.\)
c) \(d_5:\left\{{}\begin{matrix}x=3-3t\\y=2+2t\end{matrix}\right.\) và \(d_6:3x-2y+6=0\).
Giải:
a) Gọi \(\alpha\) là góc giữa hai đường thẳng \(d_1\) và \(d_2\).
Ta có \(\overrightarrow{n_{d_1}}=\left(\sqrt{3};-1\right)\), \(\overrightarrow{n_{d_2}}=\left(1;-\sqrt{3}\right)\).
Theo công thức tính góc giữa hai đường thẳng ta có
\(\cos\alpha=\left|\cos\left(\overrightarrow{n_{d_1}},\overrightarrow{n_{d_2}}\right)\right|=\dfrac{\left|\overrightarrow{n_{d_1}}.\overrightarrow{n_{d_2}}\right|}{\left|\overrightarrow{n_{d_1}}\right|.\left|\overrightarrow{n_{d_2}}\right|}=\dfrac{\left|\sqrt{3}.1+\left(-1\right).\left(-\sqrt{3}\right)\right|}{\sqrt{3+1}.\sqrt{1+3}}=\dfrac{\left|2\sqrt{3}\right|}{4}=\dfrac{\sqrt{3}}{2}\)
suy ra \(\alpha=30^o\).
Vậy góc giữa hai đường thẳng là \(\alpha=30^o\).
b) Gọi \(\beta\) là góc giữa hai đường thẳng \(d_3\) và \(d_4\).
Ta có \(\overrightarrow{u_{d_3}}=\left(3;1\right)\), \(\overrightarrow{u_{d_4}}=\left(4;-2\right)\).
Theo công thức tính góc giữa hai đường thẳng ta có
\(\cos\beta=\left|\cos\left(\overrightarrow{u_{d_3}},\overrightarrow{u_{d_4}}\right)\right|=\dfrac{\left|\overrightarrow{u_{d_3}}.\overrightarrow{u_{d_4}}\right|}{\left|\overrightarrow{u_{d_3}}\right|.\left|\overrightarrow{u_{d_4}}\right|}=\dfrac{\left|3.4+1.\left(-2\right)\right|}{\sqrt{3^2+1^2}.\sqrt{4^2+\left(-2\right)^2}}=\dfrac{\left|10\right|}{\sqrt{10}.\sqrt{20}}=\dfrac{\sqrt{2}}{2}\)
suy ra \(\beta=45^o\).
Vậy góc giữa hai đường thẳng là \(\beta=45^o\).
c) Gọi \(\gamma\) là góc giữa hai đường thẳng \(d_5\) và \(d_6\).
Ta có \(\overrightarrow{u_{d_5}}=\left(-3;2\right)\Rightarrow\overrightarrow{n_{d_5}}=\left(2;3\right)\), \(\overrightarrow{n_{d_6}}=\left(3;-2\right)\).
Theo công thức tính góc giữa hai đường thẳng ta có
\(\cos\gamma=\left|\cos\left(\overrightarrow{n_{d_5}},\overrightarrow{n_{d_6}}\right)\right|=\dfrac{\left|\overrightarrow{n_{d_5}}.\overrightarrow{n_{d_6}}\right|}{\left|\overrightarrow{n_{d_5}}\right|.\left|\overrightarrow{n_{d_6}}\right|}=\dfrac{\left|2.3+3.\left(-2\right)\right|}{\sqrt{2^2+3^2}.\sqrt{3^2+\left(-2\right)^2}}=0\)
suy ra \(\gamma=90^o\).
Vậy góc giữa hai đường thẳng là \(\gamma=90^o\).
Cách khác: Ta thấy \(\overrightarrow{n_{d_5}}.\overrightarrow{n_{d_6}}=2.3+3.\left(-2\right)=0\) do đó \(\gamma=90^o\).
4. Khoảng cách từ một điểm đến một đường thẳng
Trong mặt phẳng \(Oxy\), cho đường thẳng \(\Delta\) có phương trình \(ax+by+c=0\) (\(a^2+b^2>0\)) và điểm \(M_0\left(x_0;y_0\right)\). Khoảng cách từ điểm \(M_0\) đến đường thẳng \(\Delta\), kí hiệu là \(d\left(M_0;\Delta\right)\) được tính bởi công thức:
\(d\left(M_0;\Delta\right)=\dfrac{\left|ax_0+by_0+c\right|}{\sqrt{a^2+b^2}}\).
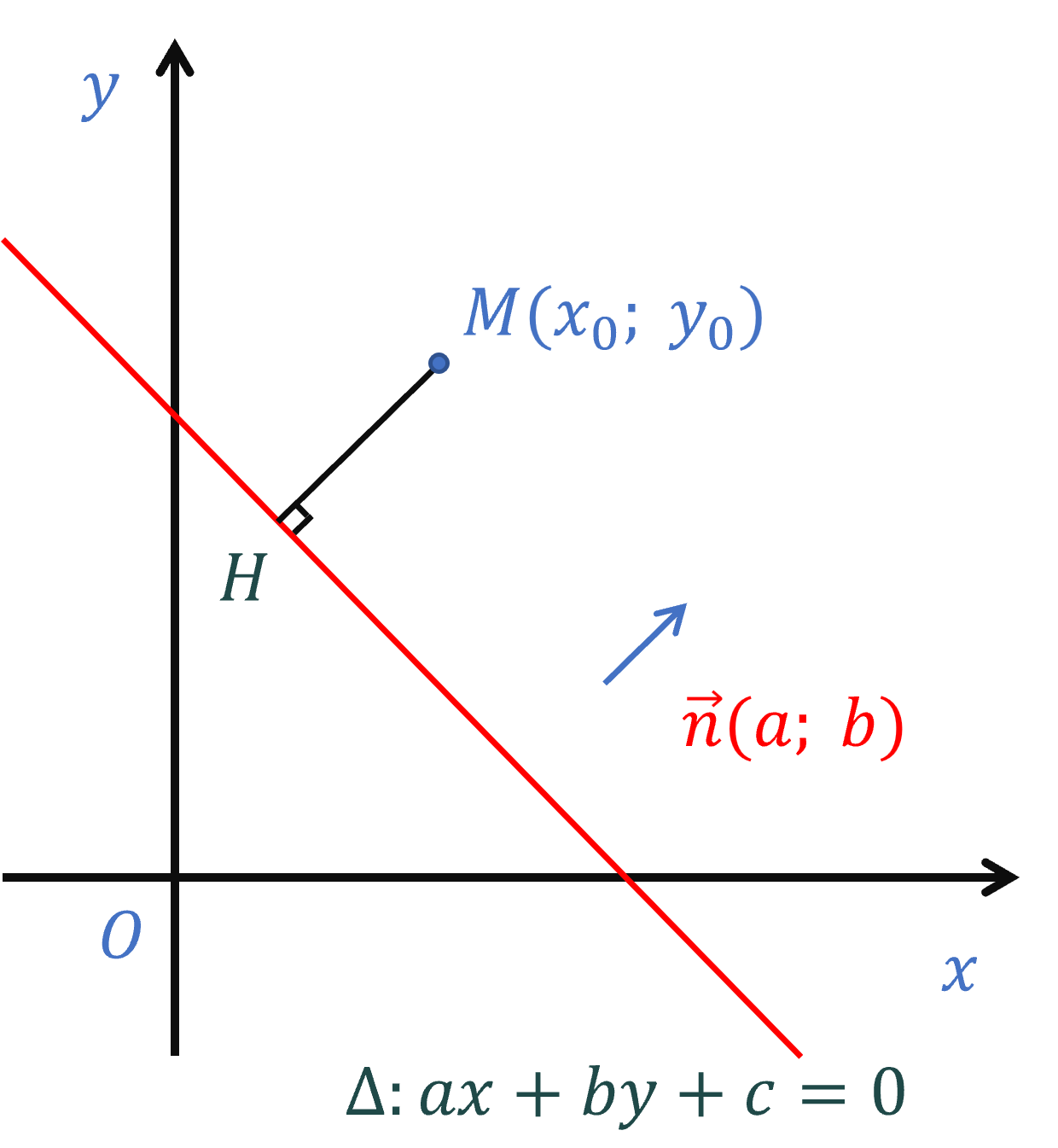
Ví dụ: Trong mặt phẳng tọa độ, cho tam giác \(ABC\) có \(A\left(1;0\right)\), \(B\left(3;2\right)\) và \(C\left(-2;-1\right)\).
Tính độ dài đường cao kẻ từ \(C\) của tam giác \(ABC\).
Giải:
Một vectơ chỉ phương của đường thẳng \(AB\) là \(\overrightarrow{AB}=\left(2;2\right)\) suy ra một vectơ pháp tuyến của đường thẳng \(AB\) là \(\overrightarrow{n_{AB}}=\left(1;-1\right)\).
Phương trình tổng quát của đường thẳng \(AB\) là \(x-y-1=0\).
Độ dài đường cao kẻ từ \(C\) của tam giác \(ABC\) là
\(d\left(C,AB\right)=\dfrac{\left|-2-\left(-1\right)-1\right|}{\sqrt{\left(-2\right)^2+\left(-1\right)^2}}=\dfrac{4\sqrt{5}}{5}\).
Bạn có thể đăng câu hỏi về bài học này ở đây
