Báo cáo học liệu
Mua học liệu
Mua học liệu:
-
Số dư ví của bạn: 0 coin - 0 Xu
-
Nếu mua học liệu này bạn sẽ bị trừ: 2 coin\Xu
Để nhận Coin\Xu, bạn có thể:

Chuyển động ném SVIP
I. Chuyển động ném ngang
1. Khái niệm chuyển động ném ngang
Chuyển động ném ngang là chuyển động có vận tốc ban đầu theo phương nằm ngang và chuyển động dưới tác dụng của trọng lực.
2. Thí nghiệm
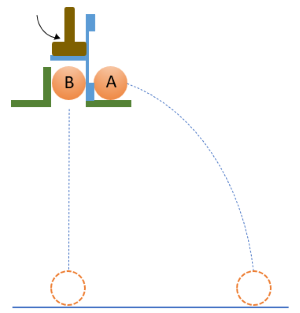
Bi B được thanh thép đàn hồi ép vào vật đỡ. Khi dùng búa đập nhẹ vào thanh thép, thanh thép không ép vào bi B nữa làm bi B rơi tự do, đồng thời đẩy bi A theo phương nằm ngang khỏi giá đỡ với vận tốc \(\text{v}_0\). Cả hai viên bi đều chạm đất cùng một lúc.

Phân tích ảnh chụp hoạt nghiệm trên giúp so sánh chuyển động rơi tự do của bi B (sự thay đổi vị trí của bi B theo phương thẳng đứng) với vận tốc ban đầu \(\text{v}_{0y}\) với sự thay đổi vị trí theo phương thẳng đứng của viên bi A bị ném ngang với vận tốc ban đầu theo phương nằm ngang \(\text{v}_{0x}=\text{v}_0\).
3. Phân tích kết quả thí nghiệm
Phân tích chuyển động của vật bị ném ngang thành hai chuyển động thành phần: chuyển động thành phần theo phương thẳng đứng và chuyển động thành phần theo phương nằm ngang. Hai chuyển động thành phần này độc lập với nhau.
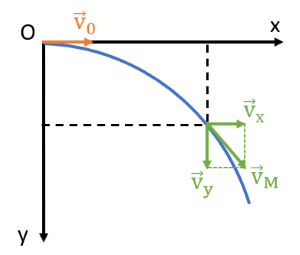
a. Thành phần chuyển động theo phương thẳng đứng
Nếu bỏ qua sức cản của không khí thì chuyển động thành phần theo phương thẳng đứng của vật là chuyển động rơi tự do với vận tốc ban đầu bằng 0.
Nếu chọn chiều dương là chiều từ trên xuống và gọi H là độ cao của vật khi bị ném ngang thì:
\(H=\dfrac{1}{2}.g.t^2\Rightarrow t=\sqrt{\dfrac{2H}{g}}\)
Công thức trên cho thấy:
- Thời gian rơi của vật bị ném ngang chỉ phụ thuộc độ cao H của vật khi bị ném, không phụ thuộc vận tốc ném.
- Nếu từ cùng một độ cao, đồng thời ném ngang các vật khác nhau với các vận tốc khác nhau thì chúng đều rơi xuống đất cùng một lúc.
b. Thành phần chuyển động theo phương nằm ngang
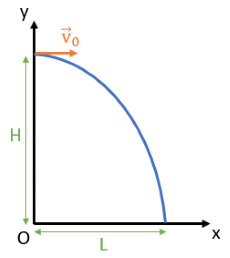
Nếu chọn chiều dương là chiều ném viên bi thì độ dịch chuyển trong chuyển động thành phần nằm ngang là:
\(d_x=v_x.t=v_0.t\)
Giá trị cực đại của độ dịch chuyển trong chuyển động thành phần nằm ngang được gọi là tầm xa L của chuyển động ném ngang:
\(L=d_{xmax}=v_0.t_{max}\),
Do đó: \(L=\text{v}_0\sqrt{\dfrac{2.H}{g}}\)
Công thức trên cho thấy:
- Tầm xa của vật bị ném ngang phụ thuộc vào độ cao H của vật khi bị ném và vận tốc ném. Nếu từ cùng một độ cao đồng thời ném các vật khác nhau với vận tốc khác nhau thì vật nào có vận tốc ném lớn hơn sẽ có tầm xa lớn hơn.
- Nếu từ các độ cao khác nhau ném ngang các vật với cùng vận tốc thì vật nào được ném ở độ cao lớn hơn sẽ có tầm xa lớn hơn.
II. Chuyển động ném xiên
Khi đá một quả bóng lên cao theo phương xiên góc với phương nằm ngang, người ta thấy quả bóng bay lên rồi rơi xuống theo một quỹ đạo có dạng hình parabol. Chuyển động của quả bóng trong trường hợp này gọi là chuyển động của vật bị ném xiên, gọi tắt là chuyển động ném xiên.
1. Phân tích chuyển động ném xiên
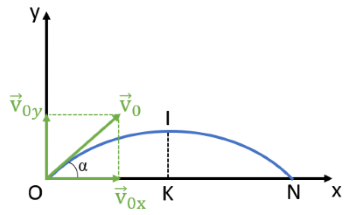
Phân tích chuyển động ném xiên thành hai chuyển động thành phần: chuyển động thành phần theo phương thẳng đứng và chuyển động thành phần theo phương nằm ngang.
2. Công thức xác định tầm cao và tầm xa của chuyển động ném xiên
Tầm cao: \(H=d_{ymax}=\dfrac{v_0^2sin^2\alpha}{2.g}\)
Tầm xa: \(L=d_{xmax}=\dfrac{v_0^2.sin2\alpha}{g}\)
1. Thời gian rơi và tầm xa của chuyển động ném ngang: \(t=\sqrt{\dfrac{2H}{g}}\); \(L=\text{v}_0\sqrt{\dfrac{2.H}{g}}\).
2. Tầm cao và tầm xa của chuyển động ném xiên: \(H=d_{ymax}=\dfrac{v_0^2sin^2\alpha}{2.g}\); \(L=d_{xmax}=\dfrac{v_0^2.sin2\alpha}{g}\).
Bạn có thể đăng câu hỏi về bài học này ở đây
