Xét sự truyền của một chùm tia sáng hẹp đơn sắc qua một lăng kính 

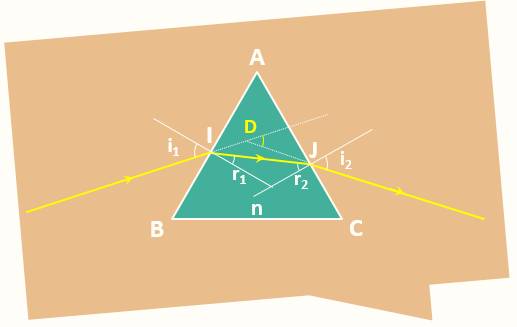
Chiếu đến mặt bên của lăng kính một chùm sáng hẹp đơn sắc SI. Khi có tia ló ra khỏi lăng kính thì tia ló bao giờ cũng lệch về phía đáy của lăng kính so với tia tới.

3. Các công thức của lăng kính

\( \begin{cases} \sin i_1 = n\sin r_1\\ \sin i_2 = n \sin r_2\\ A=r_1+r_2\\ D = i_1+i_2-A\\ \end{cases}\)

II. Thấu kính mỏng

Thấu kính là một khối chất trong suốt (thủy tinh, nhựa...) giới hạn bới hai mặt cong hoặc bởi một mặt cong và một mặt phẳng.

Theo hình dạng, thấu kính gồm hai loại:

• Thấu kính lồi (thấu kính rìa mỏng) gọi là thấu kính hội tụ

• Thấu kính lõm (thấu kính rìa dày) gọi là thấu kính phân kì

1. Các trường hợp tạo ảnh bởi thấu kính 

• Tính chất ảnh tạo bởi thấu kính hội tụ

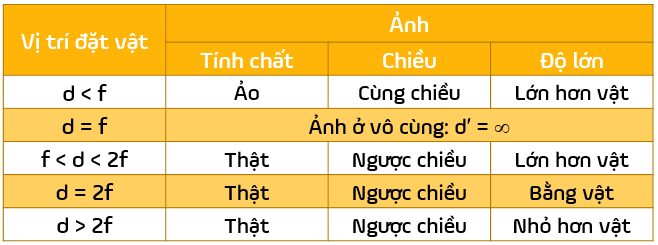
• Tính chất ảnh tạo bởi thấu kính phân kì 

Ảnh tạo bởi thấu kính phân kì luôn là ảnh áo, cùng chiều và nhỏ hơn vật.

2. Các công thức về thấu kính

Để thiết lập các công thức tổng quát áp dụng cho mọi trường hợp, người ta đặt các giá trị đại số cho khoảng cách như sau

\(\overline{OA}=d\)  với quy ước 

• \(d>0\) nếu vật thật
• \(d< 0\) nếu vật ảo (không xét)

\(\overline{OA'}=d'\)  với quy ước 

• \(d'>0\) nếu ảnh thật
• \(d'< 0\) nếu ảnh ảo 

Chiều và độ lớn của ảnh được xác định bởi tỉ số 

\(\frac{\overline{A'B'}}{\overline{AB}}=k\)

\(k\) gọi là số phóng đại ảnh

• \(k>0\): vật và ảnh cùng chiều
• \(k< 0\): vật và ảnh ngược chiều

a. Công thức xác định vị trí ảnh

\(\dfrac{1}{f}=\dfrac{1}{d}+\dfrac{1}{d'}\)

b. Công thức xác định số phóng đại ảnh

 \(k=-\dfrac{d'}{d}\)

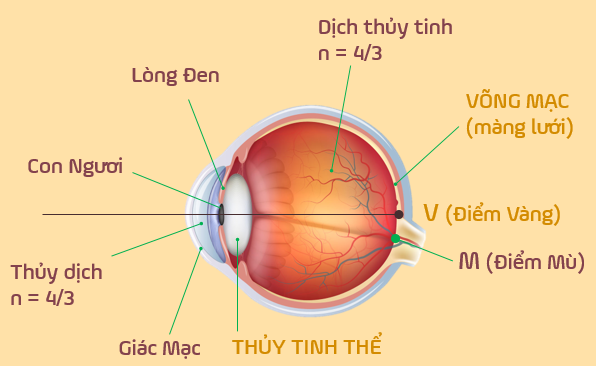
Hệ quang học của mắt được coi tương đương với một thấu kính hội tụ, gọi là thấu kính mắt.

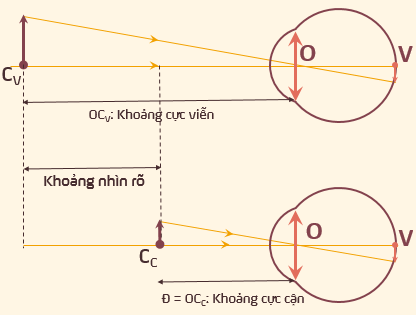
2. Điểm cực viễn. Điểm cực cận

3. Các tật của mắt và cách khắc phục 

a. Mắt cận và cách khắc phục

Đeo thấu kính phân kì có độ tụ thích hợp để có thể nhìn rõ vật ở vô cực mà mắt không phải điều tiết.

Tiêu cự của thấu kính cần đeo (nếu coi kính đeo sát mắt) là

 \({{f}_{k}}=-O{{C}_{V}}\)

b. Mắt viễn thị và cách khắc phục

Đeo một thấu kính hội tụ có tụ số thích hợp để:

• Hoặc nhìn rõ các vật ở xa mà không phải điều tiết mắt.
• Hoặc nhìn rõ được vật ở gần như mắt bình thường (ảnh ảo của điểm gần nhất muốn quan sát qua thấu kính hiện ra ở điểm cực cận của mắt).

c. Mắt lão và cách khắc phục

Khi tuổi cao khả năng điều tiết giảm vì cơ mắt yếu đi và thể thủy tinh cứng hơn nên điểm cực cận \(C_C\) dời xa mắt.

Để khắc phục tật lão thị, phải đeo kính hội tụ để nhìn rõ vật ở gần như mắt bình thường.

 Người có mắt cận khi lớn tuổi phải đeo kính hai tròng.

IV. Kính lúp

Kính lúp là dụng cụ quang bỗ trợ cho mắt để quan sát các vật nhỏ.

Kính lúp được cấu tạo bởi một thấu kính hội tụ (hoặc hệ ghép tương đương với thấu kính hội tụ) có tiêu cự nhỏ (cm).

Khi quan sát vật nhỏ qua kính lúp, mắt nhìn ảnh ảo của vật đó qua kính. Do đó cần đặt vật trong khoảng từ quang tâm đến tiêu điểm vật của kính lúp. Ngoài ra, ảnh phải có vị trí nằm trong khoảng nhìn rõ của mắt.

• Xét trường hợp ngắm chừng ở vô cực. Khi đó vật AB phải đặt ở tiêu diện vật của kính lúp.

Ta có: \(\tan \alpha =\dfrac{AB}{f}\) và \(\tan {{\alpha }_{0}}=\dfrac{AB}{O{{C}_{C}}}\)

\(\Rightarrow\) \({{G}_{\infty }}=\dfrac{\tan \alpha }{\tan {{\alpha }_{0}}}=\dfrac{O{{C}_{C}}}{f}\)

Người ta thường lấy khoảng cực cận \(O{{C}_{C}}\)= 25 cm. Khi sản xuất kính lúp người ta thường ghi giá trị \({{G}_{\infty }}\) ứng với khoảng cực cận này trên kính (5x, 8x, 10x, …).

V. Kính hiển vi

Kính hiển vi là dụng cụ quang học bỗ trợ cho mắt để nhìn các vật rất nhỏ, bằng cách tạo ra ảnh có góc trông lớn. Số bội giác của kính hiển vi lớn hơn nhiều so với số bội giác của kính lúp.

Kính hiển vi gồm hai bộ phận chính:

• Vật kính \(L_1\) là thấu kính hội tụ có tiêu rất nhỏ (vài mm)
• Thị kính \(L_2\) là một kính lúp dùng để quan sát ảnh của vật tạo bởi vật kính

Vật kính và thị kính đặt đồng trục, khoảng cách giữa chúng \({{O}_{1}}{{O}_{2}}=l\) không đổi.

Khoảng cách \(F_{1}^{'}{{F}_{2}}=\delta \) gọi là độ dài quang học của kính.

Khi ngắm chừng ở vô cực số bội giác của kính là:

 \({{G}_{\infty }}=\left| {{k}_{1}} \right|{{G}_{2}}=\dfrac{\delta .Đ}{{{f}_{1}}{{f}_{2}}}\)

  Với \(\delta ={Đ}-{{f}_{1}}-{{f}_{2}}\)

VI. Kính thiên văn

Kính thiên văn là dụng cụ quang bổ trợ cho mắt, có tác dụng tạo ảnh có góc trông lớn đối với các vật ở xa.

Kính thiên văn có hai bộ phận chính:

• Vật kính \(L_1\) là thấu kính hội tụ có tiêu cự lớn (có thể đến hàng chục mét)
• Thị kính \(L_2\) là một kính lúp để quan sát ảnh tạo bởi vật kính

Vật kính và thị kính đặt đồng trục, khoảng cách giữa chúng thay  đổi được.

Khi ngắm chừng ở vô cực:

Ta có:  \(\tan {{\alpha }_{0}}=\dfrac{{{A}_{1}}{{B}_{1}}}{{{f}_{1}}};\,\,\,\,\,\tan \alpha =\dfrac{{{A}_{1}}{{B}_{1}}}{{{f}_{2}}}\)

\(\Rightarrow\)\({{G}_{\infty }}=\dfrac{\tan \alpha }{\tan \,{{\alpha }_{0}}}=\dfrac{{{f}_{1}}}{{{f}_{2}}}\)

Số bội giác của kính thiên văn trong điều kiện này không phụ thuộc vị trí đặt mắt sau thị kính.