Bài học cùng chủ đề
Báo cáo học liệu
Mua học liệu
Mua học liệu:
-
Số dư ví của bạn: 0 coin - 0 Xu
-
Nếu mua học liệu này bạn sẽ bị trừ: 2 coin\Xu
Để nhận Coin\Xu, bạn có thể:

Kiểm tra cuối chương III SVIP
Yêu cầu đăng nhập!
Bạn chưa đăng nhập. Hãy đăng nhập để làm bài thi tại đây!
Tốc độ của 20 xe hơi khi đi qua một trạm kiểm tra tốc độ được thống kê lại như sau:
Tốc độ (km/h) | giá trị đại diện | Tần số |
[42;46) | 44 | 3 |
[46;50) | 48 | 7 |
[50;54) | 52 | 4 |
[54;58) | 56 | 3 |
[58;62) | 60 | 3 |
Biết tốc độ trung bình của 20 xe nói trên là 51,2 km/h. Phương sai của bảng số liệu ghép nhóm đã cho là
Bảng sau thống kê cân nặng của 30 quả đu đủ được lựa chọn ngẫu nhiên sau khi thu hoạch ở vườn nhà Lan.
| Cân nặng (g) | Số quả bưởi |
| [750;800) | 5 |
| [800;850) | 10 |
| [850;900) | 5 |
| [900;950) | 8 |
| [950;1000) | 2 |
Khoảng biến thiên của mẫu số liệu ghép nhóm trên là
Thống kê số thẻ vàng của mỗi câu lạc bộ trong giải ngoại hạng Anh mùa giải 2021 – 2022 cho kết quả sau:
| Số thẻ vàng | Tần số |
| [40;50) | 2 |
| [50;60) | 5 |
| [60;70) | 7 |
| [70;80) | 5 |
| [80;90) | 0 |
| [90;100) | 0 |
| [100;110) | 1 |
Khoảng biến thiên của mẫu số liệu trên là
Số tiết tự học tại nhà trong 1 tuần của 20 học sinh lớp 10 trường THPT A được ghi lại như sau:
9 | 15 | 11 | 12 | 16 | 12 | 10 | 14 | 14 | 15 |
16 | 13 | 16 | 8 | 9 | 11 | 10 | 12 | 18 | 18 |
Độ lệch chuẩn là
Tìm hiểu thời gian xem ti vi trong tuần của một số học sinh thu được kết quả sau:
Thời gian (giờ) | Số học sinh |
[0;5) | 8 |
[5;10) | 16 |
[10;15) | 4 |
[15;20) | 2 |
[20;25) | 2 |
Độ lệch chuẩn của mẫu số liệu được làm tròn đến chữ số thập phân thứ hai là
Thời gian truy cập Internet mỗi buổi tối của một số học sinh được thống kê ở bảng sau:
Thời gian | Số họ sinh |
[10,5;12,5) | 3 |
[12,5;14,5) | 12 |
[14,5;16,5) | 15 |
[16,5;18,5) | 24 |
[18,5;20,5) | 2 |
Phương sai của mẫu số liệu trên là
Trong thực hành đo hiệu điện thế của mạch điện, An và Bình đã dùng hai vôn kế khác nhau để đo, mỗi bạn tiến hành đo 10 lần và cho kết quả như sau:
Hiệu điện thế | Số lần An đo | Số lần Bình đo |
[3,85;3,90) | 1 | 1 |
[3,90;3,95) | 6 | 3 |
[3,95;4,00) | 2 | 4 |
[4,00;4,05) | 1 | 2 |
Độ lệch chuẩn của các mẫu số liệu ghép nhóm cho kết quả đo của An và Bình lần lượt là
Một cửa hàng cho thuê truyện đã thống kê số lượng truyện được thuê mỗi ngày trong ba tháng ở bảng sau.
Số truyện | Số ngày |
[16;21) | 3 |
[21;26) | 6 |
[26;31) | 15 |
[31;36) | 27 |
[36;41) | 22 |
[41;46) | 14 |
Phương sai của mẫu số liệu ghép nhóm là
Cho biểu đồ thống kê chiều cao của học sinh nữ lớp 12A:
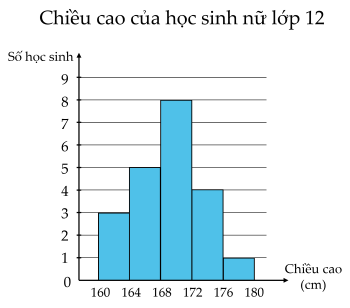
Phương sai của mẫu số liệu trên (làm tròn đến chữ số hàng phần trăm) bằng
Thống kê độ tuổi tập thể dục thể thao hàng ngày trong một cụm dân cư có bảng số liệu sau:
Độ tuổi | Số người |
[10;20) | 10 |
[20;30) | 6 |
[30;40) | 15 |
[40;50) | 19 |
[50;60) | 25 |
Phương sai của mẫu số liệu trên (kết quả làm tròn đến hàng phần trăm) là
Bảng sau thống kê cân nặng của 30 học sinh lớp 12A1.
| Cân nặng | Số học sinh |
| [45;50) | 5 |
| [50;55) | 10 |
| [55;60) | 5 |
| [60;65) | 8 |
| [65;70) | 2 |
Khoảng biến thiên của mẫu số liệu ghép nhóm trên là
Hằng ngày ông Thắng đều đi xe buýt từ nhà đến cơ quan. Dưới đây là bảng thống kê thời gian của 100 lần ông Thắng đi xe buýt từ nhà đến cơ quan.
|
Thời gian (phút) |
Số lần |
| [15;18) | 22 |
| [18;21) | 38 |
| [21;24) | 27 |
| [24;27) | 8 |
| [27;30) | 4 |
| [30;33) | 1 |
Khoảng tứ phân vị của mẫu số liệu ghép nhóm trên (làm tròn đến hàng phần trăm) bằng
Người ta ghi lại tốc độ của 40 ô tô khi đi qua một trạm đo tốc độ và có được bảng số liệu sau:
48,5 | 43 | 50 | 55 | 45 | 60 | 53 | 55,5 |
44 | 65 | 51 | 62,5 | 41 | 44,5 | 57 | 57 |
68 | 49 | 46,5 | 53,5 | 61 | 49,5 | 54 | 62 |
59 | 56 | 47 | 50 | 60 | 61 | 49,5 | 52,5 |
57 | 47 | 50 | 55 | 45 | 47,5 | 48 | 61,5 |
Ghép nhóm bảng số liệu trên thành các nhóm có độ rộng bằng nhau và nhóm đầu tiên là nửa khoảng [40;45) thì khoảng biến thiên của mẫu số liệu ghép nhóm nói trên là
Khảo sát thời gian chơi thể thao trong một ngày của 40 học sinh lớp 10A giáo viên thu được một mẫu dữ liệu ghép nhóm như sau:
| Thời gian (phút) | Số học sinh |
| [30;40) | 2 |
| [40;50) | 10 |
| [50;60) | 16 |
| [60;70) | 8 |
| [70;80) | 2 |
| [80;90) | 2 |
Khoảng tứ phân vị của bảng số liệu ghép nhóm trên là
Thời gian chờ khám bệnh của các bệnh nhân tại phòng khám X được cho trong bảng sau:
| Thời gian (phút) | Số bệnh nhân |
| [0;5) | 3 |
| [5;10) | 12 |
| [10;15) | 15 |
| [15;20) | 8 |
Khoảng tứ phân vị của mẫu số liệu ghép nhóm này (làm tròn đến chữ số hàng phần trăm) là
Mẫu số liệu ghép nhóm thống kê mức lương của một công ty (đơn vị: triệu đồng) được cho trong bảng dưới đây:
| Nhóm | Tần số |
| [10;15) | 15 |
| [15;20) | 18 |
| [20;25) | 10 |
| [25;30) | 10 |
| [30;35) | 5 |
| [35;40) | 2 |
| n=60 |
Khoảng tứ phân vị của mẫu số liệu ghép nhóm trên là
Bảng sau thống kê cân nặng của 50 quả xoài được lựa chọn ngẫu nhiên sau khi thu hoạch ở một nông trường.
Cân nặng (g) | Số quả xoài |
[250;290) | 3 |
[290;330) | 13 |
[330;370) | 18 |
[370;410) | 11 |
[410;450) | 5 |
| a) Số quả xoài nặng có cân nặng trên 330 g là 34. |
|
| b) Quả xoài nặng nhất có thể có cân nặng 450 g. |
|
| c) Quả xoài nhẹ nhất có thể có cân nặng 250 g. |
|
| d) Trong 50 quả xoài trên, hiệu số cân nặng của hai quả xoài bất kì không vượt quá 200 g. |
|
Một giống cây xoan đào được trồng tại hai địa điểm A và B. Người ta thống kê đường kính thân của một số cây xoan đào 5 năm tuổi ở bảng sau:
Đường kính (cm) | Số cây trồng ở địa điểm A | Số cây trồng ở địa điểm B |
[30;32) | 25 | 0 |
[32;34) | 38 | 22 |
[34;36) | 20 | 26 |
[36;38) | 10 | 19 |
[38;40) | 7 | 14 |
| a) Số cây đường kính nằm trong khoảng [36;38) của địa điểm B lớn hơn số cây ở điểm A. |
|
| b) Khoảng biến thiên của đường kính cây trồng ở địa điểm A là 10. |
|
| c) Khoảng biến thiên của đường kính cây trồng ở địa điểm B là 10. |
|
| d) So sánh khoảng biến thiên, đường kính cây trồng ở địa điểm B phân tán hơn so với đường kính cây trồng ở địa điểm A. |
|
Thời gian chạy tập luyện cự li 100 m của hai vận động viên được cho trong bảng sau:
Thời gian (giây) | Số lần chạy của A | Số lần chạy của B |
[10;10,3) | 2 | 3 |
[10,3;10,6) | 10 | 7 |
[10,6;10,9) | 5 | 9 |
[10,9;11,2) | 3 | 6 |
| a) Thời gian trung bình của vận động viên A lớn hơn thời gian trung bình của vận động viên B. |
|
| b) Phương sai của mẫu số liệu thời gian chạy của vận động viên A nằm lớn hơn 0,05. |
|
| c) Độ lệch chuẩn của mẫu số liệu thời gian chạy của vận động viên B nhỏ hơn 0,3. |
|
| d) Dựa trên độ lệch chuẩn, vận động viên A có thành tính luyện tập ổn định hơn vận động viên B. |
|
Thống kê điểm trung bình cuối năm của các học sinh lớp 11A và 11B ở bảng sau:
Điểm | 11A (học sinh) | 11B (học sinh) |
[5;6) | 1 | 0 |
[6;7) | 0 | 6 |
[7;8) | 11 | 8 |
[8;9) | 22 | 14 |
[9;10) | 6 | 12 |
| a) Khoảng biến thiên của điểm số học sinh lớp 11A là 5. |
|
| b) Nếu so sánh theo khoảng biến thiên thì điểm trung bình của các học sinh lớp 11B ít phân tán hơn điểm trung bình của các học sinh lớp 11A. |
|
| c) Xét mẫu số liệu của lớp 11A ta có độ lệch chuẩn của mẫu số liệu ghép nhóm là 0,51. |
|
| d) Nếu so sánh theo độ lệch chuẩn thì học sinh lớp 11A có điểm trung bình ít phân tán hơn học sinh lớp 11B. |
|
An tìm hiểu hàm lượng chất béo (đơn vị: g) có trong 100 g mỗi loại thực phẩm. Sau khi thu thập dữ liệu về 60 loại thực phẩm, An lập được bảng thống kê.
| Hàm lượng chất béo (g) | Tần số |
| [2;6) | 2 |
| [6;10) | 6 |
| [10;14) | 10 |
| [14;18) | 13 |
| [18;22) | 16 |
| [22;26) | 13 |
Tính khoảng tứ phân vị của mẫu số liệu trên. (Làm tròn đến chữ số thập phân thứ nhất)
Trả lời: .
Bảng thống kê cân nặng của 50 quả xoài được lựa chọn ngẫu nhiên sau khi thu hoạch ở nông trường như sau:
| Cân nặng (g) | Số quả xoài |
| [250;290) | 2 |
| [290;330) | 12 |
| [330;370) | 19 |
| [370;410) | 12 |
| [410;450) | 5 |
Tìm khoảng tứ phân vị của mẫu số liệu ghép nhóm trên.
Trả lời: .
Cho bảng mẫu số liệu ghép nhóm sau:
| Nhóm | Tần số |
| [20;26) | 7 |
| [26;32) | 9 |
| [32;38) | 5 |
| [38;44) | 4 |
| [44;50) | 11 |
Tính độ lệch chuẩn của mẫu số liệu ghép nhóm trên. (Làm tròn kết quả đến chữ số hàng phần trăm)
Trả lời:
Cho biểu đồ thống kê chiều cao của học sinh nữ lớp 12A:

Tính độ lệch chuẩn của mẫu số liệu trên. (Làm tròn kết quả đến chữ số hàng phần trăm)
Trả lời: .
