Bài học cùng chủ đề
Báo cáo học liệu
Mua học liệu
Mua học liệu:
-
Số dư ví của bạn: 0 coin - 0 Xu
-
Nếu mua học liệu này bạn sẽ bị trừ: 2 coin\Xu
Để nhận Coin\Xu, bạn có thể:

Kiểm tra cuối chương II SVIP
Yêu cầu đăng nhập!
Bạn chưa đăng nhập. Hãy đăng nhập để làm bài thi tại đây!
Trong không gian Oxyz cho a=i−2k. Tọa độ a là
Trong không gian Oxyz, cho A(1;2;−3),B(3;−5;2). Tọa độ vectơ AB là
Trong không gian Oxyz, cho điểm M(4;−1;7), Gọi M′ là điểm đối xứng với M qua trục Ox. Độ dài đoạn MM′ bằng bao nhiêu?
Trong không gian với hệ toạ độ Oxyz, cho vectơ u=2i−3j+6k. Độ dài của vectơ u là
Trong không gian với hệ tọa độ Oxyz, cho hình chữ nhật OKMN.
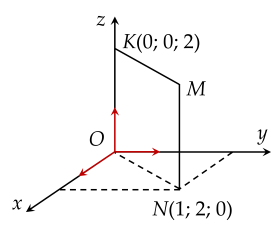
Tọa độ đỉnh M của hình chữ nhật là
Trong không gian với hệ tọa độ Oxyz, cho OM=(1;5;2), ON=(3;7;−4). Gọi P là điểm đối xứng với M qua N. Tọa độ điểm P là
Trong không gian với hệ tọa độ Oxyzcho A(−1;2;3), B(1;0;2). Tọa độ điểm M thỏa mãn AB=2.MA là điểm nào dưới đây?
Trong không gian Oxyz, cho các vectơ a=(1;−1;2), b=(3;0;−1) và c=(−2;5;1). Toạ độ của vectơ u=a+b−c là:
Cho hình lập phương ABCD.A1B1C1D1 có tâm O. Đẳng thức nào sau đây đúng?
Trong không gian, cho hình hộp ABCD.A′B′C′D′. Mệnh đề nào dưới đây sai?
Cho hai vectơ u,v có ∣u∣=3,∣v∣=4 và góc giữa hai vectơ u,v bằng 60∘. Tích vô hướng u.v bằng
Trong không gian cho a và b là hai vectơ cùng hướng và đều khác vectơ 0. Mệnh đề nào sau đây đúng?
Trong không gian với hệ toạ độ Oxyz, cho a=(2;3;1), b=(−1;5;2), c=(4;−1;3) và x=(−3;22;5). Đẳng thức nào đúng trong các đẳng thức sau?
Trong không gian Oxyz, cho tọa độ điểm A(3;−2;1). Gọi H là hình chiếu của điểm A trên trục Ox. Độ dài đoạn thẳng AH bằng
Trong không gian với hệ trục tọa độ Oxyz, cho tam giác ABC có ba đỉnh A(−1;1;−3), B(4;2;1), C(3;0;5). Tọa độ trọng tâm G của tam giác ABC là
Cho hình lăng trụ ABC.A′B′C′. Gọi M là trung điểm của cạnh BB′. Đặt CA=a, CB=b, AA′=c. Khẳng định nào sau đây đúng?
Trong không gian Oxyz, cho M(8;4;3).
(Nhấp vào ô màu vàng để chọn đúng / sai)| a) Hình chiếu vuông góc của M trên trục Ox là điểm (0;4;3). |
|
| b) Hình chiếu vuông góc của M trên trục Oz là điểm (0;0;3). |
|
| c) Hình chiếu vuông góc của M trên mặt phẳng Oxz là điểm (8;0;3). |
|
| d) OM=8i+4j+3k. |
|
Cho hình hộp ABCD.A′B′C′D′. Gọi I và K lần lượt là tâm của hình bình hành ABB′A′ và BCC′B′.

| a) IK=21AC. |
|
| b) IK=21A′C′. |
|
| c) BD+2IK=BC. |
|
| d) Ba vectơ BD;IK;B′C′ không đồng phẳng. |
|
Cho tứ diện OABC có các cạnh OA,OB,OC đôi một vuông góc và OA=OB=OC=a. Gọi M,N lần lượt là trung điểm các cạnh AB,OC.
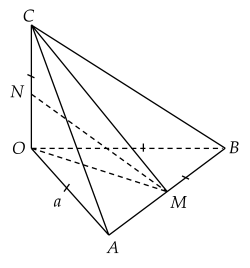
| a) MN=21(OA+BC). |
|
| b) cos(OM,CM)=33. |
|
| c) MN.OA=−2a2. |
|
| d) ∣CB+OA∣=a2. |
|
Trong không gian Oxyz, một viên đạn được bắn ra từ vị trí A(1;2;3) hướng đến vị trí B(0;1;−6), bia chắn là mặt phẳng (P):4x−y+2z+13=0, đơn vị là kilômét.
(Nhấp vào ô màu vàng để chọn đúng / sai)| a) Hình chiếu vuông góc của A trên (Oxy) là H(0;2;3). |
|
| b) Góc giữa đường thẳng AB và mặt phẳng (P) (làm tròn đến hàng đơn vị) là 60∘. |
|
| c) Điểm B thuộc mặt phẳng (P). |
|
| d) Giả sử viên đạn chuyển động thẳng đều theo hướng vectơ v(−2;−2;−18) với vận tốc 800 m/s (bỏ qua mọi lực cản và chướng ngại vật), sau một phút bắn ra đi qua điểm B. |
|
Trong không gian, cho hình lập phương ABCD.A′B′C′D′. Gọi N là điểm thỏa mãn C′N=2NB′, M là trung điểm của A′D′, I là giao điểm của A′N và B′M. Biết AI=aAA′+bAB+cAD. Tính a+b+c. (kết quả viết dưới dạng số thập phân)
Trả lời:
Cho hình hộp ABCD.A′B′C′D′ có các cạnh đều bằng a và B′A′D′=60∘,B′A′A=D′A′A=120∘. Tính số đo (đơn vị độ) của góc giữa hai đường thẳng AB với A′D.
Trả lời:
Trong không gian chọn hệ trục tọa độ cho trước, đơn vị đo lấy kilômét, ra đa phát hiện một máy bay chiến đấu của Anh di chuyển với vận tốc và hướng không đổi từ điểm M(500;200;10) đến điểm N(800;300;10) trong 20 phút. Nếu máy bay tiếp tục giữ nguyên vận tốc và hướng bay thì tọa độ của máy bay sau 4 phút tiếp là Q(a;b;c). Khi đó a+b+c bằng bao nhiêu?
Trả lời:
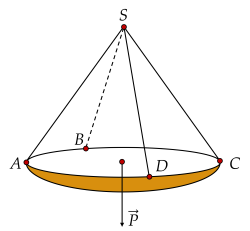
Một chiếc đèn chùm treo có khối lượng m=7 kg được thiết kế với đĩa đèn được giữ bởi bốn đoạn xích SA,SB,SC,SD sao cho S.ABCD là hình chóp tứ giác đều có ASC=60∘. Tính độ lớn của lực căng cho mỗi sợi xích khi đèn đứng yên. (Làm tròn kết quả đến chữ số thập phân thứ nhất, đơn vị N)
Trả lời:
