Báo cáo học liệu
Mua học liệu
Mua học liệu:
-
Số dư ví của bạn: 0 coin - 0 Xu
-
Nếu mua học liệu này bạn sẽ bị trừ: 2 coin\Xu
Để nhận Coin\Xu, bạn có thể:

Khoảng biến thiên và khoảng tứ phân vị SVIP

Lưu ý: Ở điểm dừng, nếu không thấy nút nộp bài, bạn hãy kéo thanh trượt xuống dưới.
Bạn phải xem đến hết Video thì mới được lưu thời gian xem.
Để đảm bảo tốc độ truyền video, OLM lưu trữ video trên youtube. Do vậy phụ huynh tạm thời không chặn youtube để con có thể xem được bài giảng.
Nội dung này là Video có điểm dừng: Xem video kết hợp với trả lời câu hỏi.
Nếu câu hỏi nào bị trả lời sai, bạn sẽ phải trả lời lại dạng bài đó đến khi nào đúng mới qua được điểm dừng.
Bạn không được phép tua video qua một điểm dừng chưa hoàn thành.
Dữ liệu luyện tập chỉ được lưu khi bạn qua mỗi điểm dừng.
Qua bài học này học sinh sẽ nắm được:
- Định nghĩa khoảng biến thiên và khoảng tứ phân vị.
- Ý nghĩa của khoảng biến thiên và khoảng tứ phân vị trong việc đo độ phân tán của mẫu số liệu.
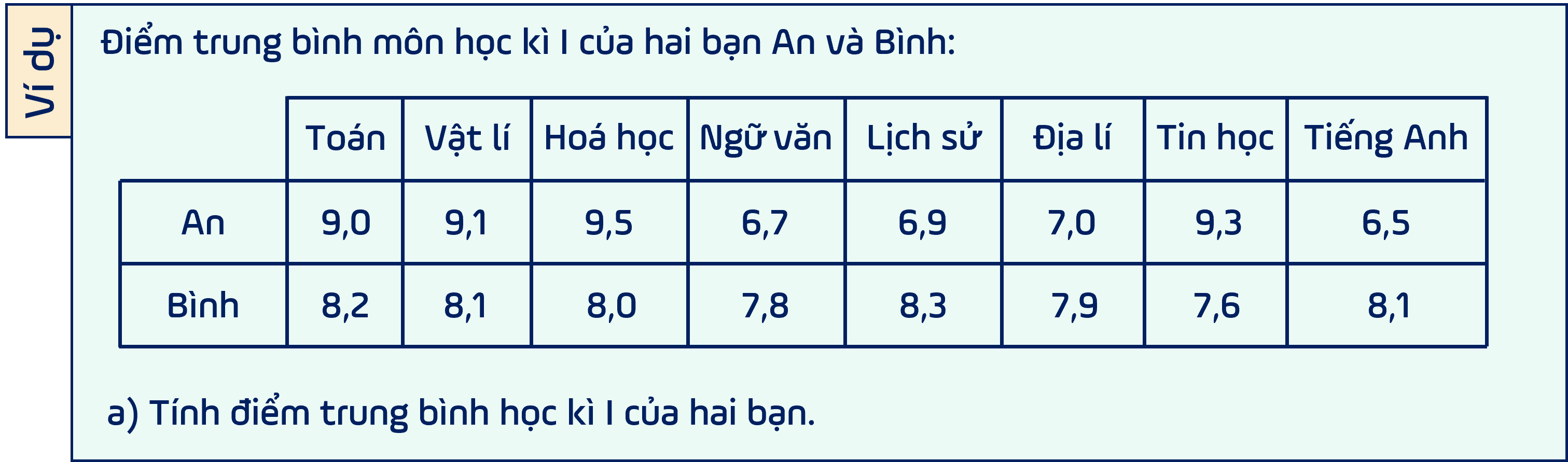
Điểm trung bình tất cả các môn học của bạn An là .
Điểm trung bình tất cả các môn học của bạn Bình là .
Cho kết quả tính điểm trung bình của hai bạn.

Từ kết quả trên, ta có thể đánh giá xem bạn nào học đều hơn không?
Cho bảng điểm của hai bạn.

Trong hàng điểm của bạn An, điểm phẩy cao nhất của An là , thấp nhất của An là .
Cho bảng điểm và công thức tính khoảng biến thiên.
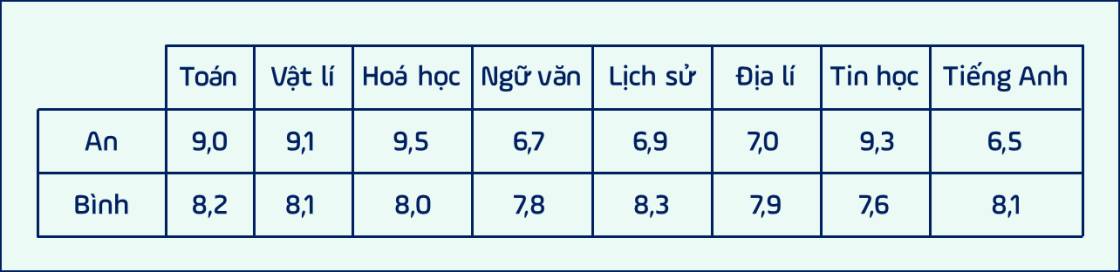

Khoảng biến thiên của mẫu số liệu điểm trung bình môn học của Bình là .

Khoảng biến thiên của mẫu số liệu trên là .

Các tứ phân vị của mẫu số liệu trên là:
Q1 = ;
Q2 = ;
Q3 = .

Ta đã tính được các tứ phân vị của mẫu số liệu trên:
Q1=36,5;
Q2=40;
Q3=43,5.
Khoảng tứ phân vị của mẫu số liệu trên là .
Văn bản dưới đây là được tạo ra tự động từ nhận diện giọng nói trong video nên có thể có lỗi
- Chào mừng các em đã quay trở lại với bài
- học mới trên trang web olm.vn và trong
- bài giảng lần này chúng ta sẽ cùng nhau
- tìm hiểu về các số đặc trưng đo độ phân
- tán
- từ khóa mà chúng ta cần chú ý ở đây là
- độ phân tán
- chúng ta sẽ đến với số đặc trưng đo độ
- phân tán đầu tiên khoảng biến thiên
- để hiểu như thế nào là khoảng biến thiên
- thì chúng ta sẽ cùng nhau đi vào ví dụ ở
- trên màn hình là điểm trung bình môn học
- kỳ 1 của hai bạn An và Bình được cho
- dưới dạng bảng như sau
- đề bài yêu cầu chúng ta tính điểm trung
- bình học kì 1 của hai bạn
- sử dụng máy tính thì chúng ta tính được
- điểm trung bình của hai bạn đều là 8
- nhưng chúng ta đã biết được bài trước số
- trung bình là một số để đo xu thế trung
- tâm
- Tuy nhiên thì liệu chúng ta có thể Căn
- cứ vào điểm trung bình để đánh giá bạn
- An và bạn bình học ngang nhau hay không
- Để hiểu hơn về vấn đề này thì chúng ta
- sẽ cùng nhau đến với câu hỏi số 2 điểm
- trung bình có thể so sánh mức độ học đều
- của hai bạn hay không Và bạn đang học
- đều hơn
- nếu như chỉ dựa vào điểm trung bình với
- điểm trung bình của hai bạn đều bằng 8
- thì ta sẽ đánh giá lực học của hai bạn
- làm ăn nhau tuy nhiên về mức độ học đều
- thì điểm trung bình không thể so sánh
- mức độ học để của hai bạn
- nếu như chúng ta Để ý kỹ vào bảng điểm
- nhìn vào bảng điểm của bạn An thì chúng
- ta có thể thấy một số môn học của bạn An
- học rất tốt
- và những môn này đều có điểm phẩy ở trên
- 9 phẩy Tuy nhiên thì bên cạnh đó một số
- môn học lại chưa được tốt lắm và điểm
- phẩy của các môn này lại không vượt quá
- 7 phẩy
- đến đây Thầy có nhận xét như sau sự
- chênh lệch điểm số của bạn An dựa những
- môn học khá là cao
- còn khi chúng ta nhìn vào bảng điểm của
- bạn mình thì sự chênh lệch điểm số giữa
- các môn học là không cao
- và Như vậy chúng ta có thể kết luận là
- bạn bình học đều hơn
- vì bạn cảm nhận là như vậy Còn nếu như
- chúng ta muốn đưa mức độ học đều về dưới
- dạng con số thì chúng ta đi vào khái
- niệm khoảng biến thiên
- khỏi biến thiên được ký hiệu là R
- là Hiệu giữa giá trị lớn nhất và giá trị
- nhỏ nhất trong mẫu số liệu
- bây giờ chúng ta sẽ cùng nhau Tính
- khoảng biến thiên của mẫu số liệu về
- điểm trung bình môn học của hai bạn An
- và Bình
- nhìn vào bảng điểm của bạn An thì chúng
- ta thấy điểm cao nhất của bạn An là điểm
- hóa học 9,5 còn điểm thấp nhất là điểm
- tiếng Anh 6,5
- như vậy khoảng biến thiên của bạn An sẽ
- là 9,5 - 6,5 bằng 3 và Điều này chứng tỏ
- điểm số của bạn An sẽ phân tán ở trên
- đoạn thẳng có độ dài bằng 3
- tương tự Chúng ta sẽ tìm khoảng biến
- thiên của điểm trung bình môn học kỳ 1
- của bạn Bình
- chúng ta có thể thấy điểm phẩy cao nhất
- của bạn Bình là điểm phẩy lịch sử
- và điểm phải thấp nhất là điểm phải tin
- học và như vậy khoảng mấy Thiên ở trong
- trường hợp này chúng ta sẽ tính được rb
- bằng 8,3 - 7,6 bằng 0,7
- và chúng ta có thể thấy điểm số của bạn
- Bình sẽ phân tán ở trên đoạn thẳng có độ
- dài bằng 0,7
- và nhìn vào các giá trị của khoảng biến
- thiên thì chúng ta có thể thấy khi
- khoảng biến thiên càng lớn thì mẫu số
- liệu sẽ càng phân tán Còn khi khoảng
- biến thiên càng nhỏ thì mẫu số liệu càng
- ít phân tán ta có nhận xét sau đây
- khoảng mấy Thiên càng lớn mẫu số liệu
- càng phân tán
- khoảng biến thiên rất dễ tính toán chúng
- ta chỉ cần tìm hiệu giữ giá trị lớn nhất
- và giá trị nhỏ nhất trong mẫu số liệu
- tuy nhiên thì việc dễ tính này có thể sẽ
- dẫn tới một điểm yếu
- và sau đây chúng ta sẽ cùng nhau đến với
- một ví dụ để chỉ ra điểm yếu của khoảng
- biến thiên
- cho mốt số liệu về lương với đơn vị là
- triệu đồng của nhân viên công ty B như
- sau
- bây giờ thầy muốn các em tính cho thầy
- khoảng mấy Thiên của mẫu số liệu này
- chúng ta thấy khoảng biến thiên của mẫu
- số liệu này sẽ là hiệu của 80 và 2 chúng
- ta sẽ được r = 78
- nếu như để ý một chút thì chúng ta có
- thể thấy là 2 và 80 là hai giá trị bất
- thường do số 2 là một số quá nhỏ so với
- phần đông của mẫu số liệu và 80 là một
- số quá lớn so với phần đông của mẫu số
- liệu
- để nhìn rõ hơn về vấn đề này thì thầy
- muốn chúng ta đến với trục số Nếu như
- thầy biểu diễn mẫu số liệu lên trên trục
- số thì ta có trục số như sau nhìn trên
- trục số thì chúng ta có thể thấy hai số
- liệu bất thường đó là 2 và 80 cách quá
- xa với phần đông của mẫu số liệu
- cụ thể hơn khi chúng ta nhìn vào hai
- đoạn từ 2 đến 35 ta thấy không có giá
- trị nào của mẫu số liệu xuất hiện trong
- khoảng này cũng tương tự với khoảng từ
- 45 cho đến 80 không có giá trị nào của
- mẫu số liệu nằm ở trên đoạn này
- như vậy chúng ta rút ra nhận xét sau đây
- khoảng biến thiên rất dễ tính nhưng cũng
- dễ bị ảnh hưởng bởi các giá trị bất
- thường
- và để hạn chế vấn đề này thì chúng ta sẽ
- đến với số đặc trưng đo độ phân tán thứ
- hai
- khoảng từ phân vị
- [âm nhạc]
- khoảng từ phân vị được ký hiệu là Delta
- Q là Hiệu giữa từ phân vị thứ ba và từ
- phân vị thứ nhất trong mẫu số liệu
- nếu như khoảng biến thiên cho chúng ta
- biết độ dài của đoạn thẳng chứa mẫu số
- liệu thì khoảng từ phân vị là Hiệu giữa
- q3 và Q1 cho chúng ta biết độ dài căng
- thẳng từ từ phân vị thứ nhất cho đến từ
- phân vị thứ ba chứa 50% mẫu số liệu đứng
- ở chính giữa
- và ta có nhận xét sau đây khoảng từ phân
- vị là khoảng biến thiên của 50% số liệu
- đường chính giữa của mẫu số liệu đã được
- sắp xếp
- và nhìn vào sơ đồ chúng ta có thể thấy
- là khoảng từ phân vị sẽ không bị ảnh
- hưởng bởi giá trị bất thường quá lớn
- hoặc quá nhỏ so với phần đông mẫu số
- liệu
- bây giờ chúng ta sẽ cùng nhau tìm khoảng
- từ phân vị của mẫu số liệu về lương của
- nhân viên công ty B
- trước khi đi tính khoảng từ phân vị thì
- chúng ta cần phải tìm từ phân vị thứ ba
- và từ phân vị thứ nhất hay nói cách khác
- Chúng ta cần phải xác định 3 từ phân vị
- của mẫu số liệu
- chúng ta tìm được 3 từ phân vị là 36,5
- 40 và 43,5 đến đây chúng ta sẽ áp dụng
- công thức tính khoảng từ phân vị là giữa
- từ phân vị thứ ba và từ phân vị thứ nhất
- q3 - Q1
- và ta được kết quả khoảng từ phân vị
- bằng 7
- ở đây cũng là nội dung cuối cùng ở trong
- phần này
Bạn có thể đăng câu hỏi về bài học này ở đây
