Báo cáo học liệu
Mua học liệu
Mua học liệu:
-
Số dư ví của bạn: 0 coin - 0 Xu
-
Nếu mua học liệu này bạn sẽ bị trừ: 2 coin\Xu
Để nhận Coin\Xu, bạn có thể:
CHÚC MỪNG
Bạn đã nhận được sao học tập

Chú ý:
Thành tích của bạn sẽ được cập nhật trên bảng xếp hạng sau 1 giờ!
Hướng dẫn ôn tập: Các đường đồng quy của tam giác (Phần 1) SVIP

Nếu video không chạy trên Zalo, bạn vui lòng Click vào đây để xem hướng dẫn
Lưu ý: Ở điểm dừng, nếu không thấy nút nộp bài, bạn hãy kéo thanh trượt xuống dưới.
Bạn phải xem đến hết Video thì mới được lưu thời gian xem.
Để đảm bảo tốc độ truyền video, OLM lưu trữ video trên youtube. Do vậy phụ huynh tạm thời không chặn youtube để con có thể xem được bài giảng.
Nội dung này là Video có điểm dừng: Xem video kết hợp với trả lời câu hỏi.
Nếu câu hỏi nào bị trả lời sai, bạn sẽ phải trả lời lại dạng bài đó đến khi nào đúng mới qua được điểm dừng.
Bạn không được phép tua video qua một điểm dừng chưa hoàn thành.
Dữ liệu luyện tập chỉ được lưu khi bạn qua mỗi điểm dừng.
Lưu ý: Ở điểm dừng, nếu không thấy nút nộp bài, bạn hãy kéo thanh trượt xuống dưới.
Bạn phải xem đến hết Video thì mới được lưu thời gian xem.
Để đảm bảo tốc độ truyền video, OLM lưu trữ video trên youtube. Do vậy phụ huynh tạm thời không chặn youtube để con có thể xem được bài giảng.
Nội dung này là Video có điểm dừng: Xem video kết hợp với trả lời câu hỏi.
Nếu câu hỏi nào bị trả lời sai, bạn sẽ phải trả lời lại dạng bài đó đến khi nào đúng mới qua được điểm dừng.
Bạn không được phép tua video qua một điểm dừng chưa hoàn thành.
Dữ liệu luyện tập chỉ được lưu khi bạn qua mỗi điểm dừng.
Theo dõi OLM miễn phí trên Youtube và Facebook:
Đây là bản xem trước câu hỏi trong video.
Hãy
đăng nhập
hoặc
đăng ký
và xác thực tài khoản để trải nghiệm học không giới hạn!
Câu 1 (1đ):
Cho tam giác ABC cân tại A và các trung tuyến BD, CE như hình vẽ.
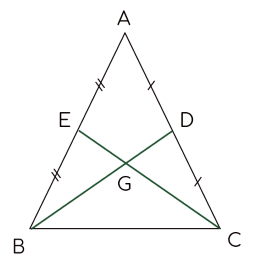
Khẳng định nào sau đây đúng?
EBC=DCB.
AB=BC.
ABC=BAC.
AE=AB.
Câu 2 (1đ):
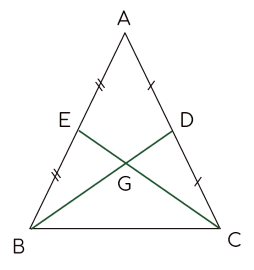
Xét ΔBCE và ΔCBD có:
BC là cạnh chung;
EBC=DCB;
Để hai tam giác trên bằng nhau theo trường hợp c.g.c, ta cần thêm yếu tố bằng nhau nào sau đây?
BEC=CDB=90∘.
BE=CD.
EC=BD.
ECB=DBC.
Câu 3 (1đ):
Cho tam giác ABC cân tại A có hai đường trung tuyến BD và CE cắt nhau tại G.
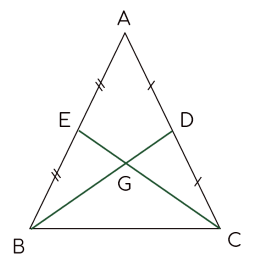
Khi đó, G là của tam giác ABC và BG = .BD.
31 trọng tâm 32 trực tâm 2 23
(Kéo thả hoặc click vào để điền)
Câu 4 (1đ):
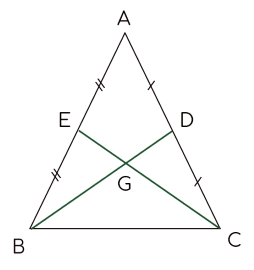
Ta có GB = 32.BD thì GD = .BD suy ra GD = .GB.
23 3 2 31 21
(Kéo thả hoặc click vào để điền)
Câu 5 (1đ):
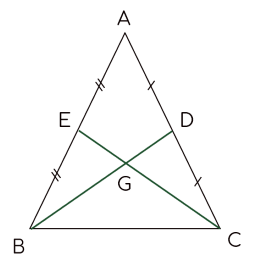
Trong tam giác GBC ta có:
GB + GC BC.
Văn bản dưới đây là được tạo ra tự động từ nhận diện giọng nói trong video nên có thể có lỗi
- Xin
- [âm nhạc]
- chào mừng em đã quay trở lại với khóe
- trên cho học trực tuyến org.vn
- trong buổi học tuần này thầy Park em sẽ
- tiếp tục ôn tập các nội dung liên quan
- tới tam giác cụ thể là các đường đồng
- quy của tam giác bao gồm có đường trung
- tuyến đường cao AH đường phân giác và
- đường trung trực
- ban học của chúng ta sẽ bao gồm 2 phần
- trong phần đầu tiên thời sẽ nhắc lại cho
- kèm các nội dung quan trọng về lý thuyết
- Sau đó chúng ta sẽ đến với các đường
- trung tuyến trong tam giác
- trước khi tới tối các đường đồng quy thì
- thay sẽ nhắc lại cho kem về 3 nội dung
- sau đây thứ nhất là bất đẳng thức trong
- tam giác trong một tam giác tổng độ dài
- hai cạnh bất kỳ thì luôn lớn hơn độ dài
- cạnh còn lại kể cả là tam giác nhọn dằng
- dặc tù hay là các tam giác đặc biệt như
- là thật cần ra đều chúng ta đều có điều
- này cho ví dụ như tam giác abc trên hình
- vẽ thì AB + AC sẽ lớn hơn BC
- bất đẳng thức trong tam giác này sẽ là
- một công cụ hiệu quả để kem giải các bài
- toán yêu cầu chứng minh các bất đẳng
- thức liên quan tới độ dài của các cách
- nội dung số hay là về đường trung trực
- đường trung trực trong tam giác thì có
- tính chất sau đây tập hợp các điểm mà
- cách đều hai đầu mút của một đoạn thẳng
- sẽ cho ta đường trung trực của đoạn
- thẳng đó ví dụ như với luận thẳng bc
- tất cả các điểm cách đều 2 đầu bút B và
- C sẽ cho ta đường thẳng d chính là đường
- trung trực của đoạn thẳng bc
- khi đó lấy một điểm A bất kỳ ở trên
- đường thẳng d ta cũng có ab bằng ac như
- vậy AB = AC kìa sẽ thụt vào đường trung
- trực của BC và ngược lại nếu những a
- thuộc vào đường trung trực D thì ib cũng
- sẽ = AC I từ
- tương tự như thấy ta có tính chất với
- đường phân giác trong tập hợp các điểm
- nằm bên trong của góc này và cách đều
- hai cạnh của góc sẽ cho ta tia phân giác
- của góc đó ví dụ trên hình vẽ góc Bac có
- điểm D điểm D nằm trong góc bé
- c&p chính là khoảng cách từ D cho đến
- cạnh AB DC là khoảng cách từ D đến cạnh
- AC Nếu BD = DC thì ID chính là tia phân
- giác của góc B AC và ngược lại nếu ta có
- AD là tiệm giác thì D sẽ cách đều hai
- cạnh AB AC tức là BB cũng bằng để xây
- đây là bà tính chất rất quan trọng và
- kem cũng cần phải nhớ nếu bạn nào còn
- chưa Nhớ những nội dung đang thì các bạn
- hãy tải file tổng hợp lý thuyết ở trên m
- để chúng ta đã qua sử dụng trong quá
- trình làm bài nhất phần tiếp theo chính
- là nội dung chính trong bài học ngày hôm
- nay thầy sẽ nhắc lại cho kem về các
- đường đồng quy của tam giác
- đầu tiên là trung tuyến ba đường trung
- tuyến của một tam giác cắt nhau tại một
- điểm Điểm đó chính là trọng tâm của tam
- giác ví dụ tam giác ABC có 3 đường trung
- tuyến AM be và CF cùng cắt nhau tại điểm
- g thì G là trọng tâm của tam giác ABC
- điểm G còn có một tính chất đó là ogg
- bằng 2/3 m tương tự như vậy trên trung
- tuyến CS chẳng hạn thì ta có c g bằng
- 2/3 CF
- tiếp theo là với đường phân giác ba
- đường phân giác của tam giác cũng cắt
- nhau tại một điểm điểm này có đặc điểm
- là cách đều 3 cạnh của tam giác đó ba
- đường phân giác
- api cùng cắt nhau tại điểm i i
- It is và im sẽ bằng nhau
- tiếp theo là ba đường trung trực
- ở ba đường trung trực của tam giác cùng
- đi qua một điểm và điểm này cách đều ba
- đỉnh của tam giác đó ba đều màu xám này
- là ba đường trung trực ứng với ba cạnh
- của tam giác chúng cùng đi qua điểm D
- điểm D sẽ cách đều ba đình ABC tức là
- đây A = DB = DC
- các bạn chú ý phân biệt nội dung số 2 và
- số 3 nhát dao của ba đường phân giác thì
- cách đều ba cạnh còn giao của ba đường
- trung trực thì cách đều ba đình
- và cuối cùng là giao điểm ba đỉnh cao sẽ
- cắt nhau tại trực tâm của tam giác
- ví dụ tam giác ABC có 3 đường cao AD be
- và CF thì chúng sẽ đồng qui tại điểm H H
- người ta gọi là trực tâm của tam giác
- ABC
- font nhìn vào cả 4 nội dung này các bạn
- chú ý phân biệt cho thành Giao ở biển là
- trọng tâm còn rọc ba đỉnh cao là trực
- tâm trọng tâm trực tâm là hai tên gọi
- đặc biệt mà các bạn cần phải nhớ tiếp
- theo phân biệt Trực tâm là giao của ba
- đường cao chứ không phải là giao của ba
- đường trung trực nhưng nhiều bạn vẫn
- nhầm lẫn nghé
- từ những nội dung lý thuyết này thầy và
- kem sẽ củng cố thông qua 4 bài tập bài
- đầu tiên Cho tam giác ABC cân tại A có
- hai đường trung tuyến BD CE cắt nhau tại
- g
- kem sẽ cùng thầy đọc để tới đâu chúng ta
- sẽ vẽ hình từ đó nhất thứ nhất và vẽ
- thần sắc ABC cân tại A này hai đường
- trung tuyến là BD và CE cắt nhau tại G D
- là trung điểm của AC ta sẽ ký hiệu nhiều
- chiến hình tương tự như vậy hay là trung
- điểm của AB và chúng cắt nhau tại điểm G
- câu a yêu cầu chứng minh BD = C
- tí bey là chứng minh tam giác remix ê ê
- chỉ cần và cuối cùng chính mình tờ đi +
- e lớn hơn 1/2 BC
- quý đầu tiên để mà chứng minh được BD =
- CE
- BD = CE
- cũng suy luận như thầy đã hướng dẫn được
- từng chữ thôi ta sẽ áp hai cạnh này vào
- hai tam giác bằng nhau
- hai tam giác có thể bằng nhau mà chứa
- pdc chính là tam giác BCD
- và tam giác
- cbd nếu như thời xét hai tam giác đó thì
- các bạn sẽ cho thầy biết giả thiết đã
- cho ta những yếu tố bằng nhau nào của
- hai tam giác trên
- chính xác rồi ta đã cổ BC là cạnh trung
- và hai góc ABC góc ABC = góc BC b bởi
- vịt đó là hai góc ở đáy của tam giác cân
- abc có một cạnh có một em chỉ ta của hai
- hướng một là sử dụng trường hợp cạnh góc
- cạnh hay là trường hợp góc-cạnh-góc thấy
- sẽ suy nghĩ theo hướng cạnh-góc-cạnh
- trước
- các bạn phát hiện cho chính xác để có
- thể sử dụng trường hợp cạnh góc cạnh ta
- cần thêm hai cạnh bằng nhau đó là be và
- CD Vậy thì pe và C D có liên quan gì tới
- giả thiết tam giác ABC cân tại A và các
- trung tuyến BD không
- tam giác ABC cân tại A thì trước tiên là
- xui được AB = AC đã sau đó E là trung
- điểm của cạnh AB thì ib sẽ bằng E hay
- nói cách khác AB sẽ bằng 2 lần b
- tương tự như vậy đây là trung điểm của
- đoạn AC thì kaycee cũng bằng hai lần CD
- mà AB thì = AC nên kem Sẽ suy ngay ra
- được be và CD bằng nhau như vậy em muốn
- đủ các yếu tố để xét hai tam giác bce và
- cbd chúng bằng nhau theo trường hợp cạnh
- góc cạnh Từ đó suy ra lượng BD = C Đây
- là hai cạnh tương ứng như vậy Ý là chúng
- ta đã giải quyết xong và kem chú ý khi
- người ta cho các giả thiết là các trung
- tuyến thì ta sẽ được phép sử dụng ngay
- các trung điểm
- A B Chứng minh tam giác gpc là tam giác
- cân
- trong đó cô Ba ta đã có thêm giả thiết
- là BD = c e Em cần gì nhớ nhá á
- ạ bây giờ để mà tam giác rồi PC cân đấy
- thì cách dễ nhất là ta đã có công an tam
- giác BCD bằng tam giác cbd nên góc ACB +
- IC B nhất và góc dbc sẽ bằng nhau vì là
- hai góc tương ứng nên suy nhanh được tam
- giác BCD là tam giác cân tại điểm G
- Ngoài ra thì còn một cách nữa là ta
- Chứng minh tam giác gpc cần Ngưng sử
- dụng yếu tố hình thành tức là ta Chứng
- minh c g = b g trong đó nhờ là giao điểm
- của hai đường trung tuyến
- thì
- các bạn trả lời rất chính xác thì g sẽ
- là trọng tâm của tam giác ABC
- và ta sử dụng tính chất của trọng tâm là
- PG sẽ bằng hai phần ba BD tương tự như
- thế CG sẽ bằng 2/3 xe mà b d và C chính
- xác rồi chúng đã bằng nhau theo câu a
- dẫn tới cgdg sẽ bằng nhau hai cạnh này
- bằng nhau thì ta có ngày tham giác gbc
- cần tại g và chúng ta đã hoàn thành ý b
- là chính mình gj + gửi lớn hơn 1/2 BC
- như thầy cũng đã chú ý khi nhắc lại phần
- lý thuyết Nếu như bài toán yêu cầu chứng
- minh liên quan tới bất đẳng thức giữa độ
- dài các cạnh các đoạn thẳng thì chúng ta
- có một công cụ có thể đi tới đó là bất
- đẳng thức trong tam giác Em gửi đi Gửi
- ABC chúng trước cùng thuộc phòng của tam
- giác vậy thì ta sẽ tìm cách đưa chúng về
- trong cùng một tam giác để sử dụng bất
- đẳng thức tam giác đó
- thì lag sẽ có liên quan tới g c g là
- trọng tâm tương tự gd liên quan tới BG
- vậy Các em có thể xét trong tam giác gbc
- nhưng trước tiền ta sẽ tìm ra mối liên
- hệ thầy đã có của b là vợ mê bằng 2/3 BD
- chính sách ta sẽ suy ra được gd khi đó
- sẽ bằng một phần ba BD chia BC thành 3
- phần cơ B chiếm hai phần thì gd Còn Lại
- Một phần như vậy gd sẽ bằng 1/2 của GB
- tương tự như thế các bạn cũng sẽ chứng
- minh được rồi E bằng 1/2 GC khi đó tính
- tổng gd + e gd + e axit có 1 phần 2 GB ở
- phần heigl save vật thể đặt một phần hay
- ra ngoài bên trong còn lại GB + GC
- Vậy thì này đưa về điều phải chứng minh
- ta sẽ xét trong tam giác rồi PC
- rất chính xác theo bất đẳng thức trong
- tam giác thì GB + GC sẽ lớn hơn BC như
- vậy một phần 2 GB + GC sẽ lớn hơn 1/2 BC
- và ta có điều phải chứng minh
K
Khách
Bạn có thể đăng câu hỏi về bài học này ở đây
Chưa có câu hỏi thảo luận nào về bài giao này
OLMc◯2022
