Hệ toạ độ không gian. Phương trình mặt cầu (nâng cao) SVIP

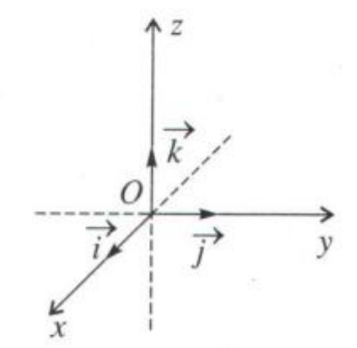
Trong không gian, cho ba trục $x'Ox, y'Oy, z'Oz$ vuông góc với nhau từng đôi một. Gọi $\overrightarrow{i}$, $\overrightarrow{i}$, $\overrightarrow{k}$ lần lượt là các vectơ đơn vị trên các trục $x'Ox, y'Oy, z'Oz$ (xem hình vẽ trên). Một điểm $M$ trong không gian thỏa mãn $\overrightarrow{OM}=-6\overrightarrow{j}+3\overrightarrow{k}$. Trong các khẳng định sau, khẳng định nào đúng?

Trong không gian $Oxyz$ cho tam giác $ABC$ với $A(4;-4;-1)$, $B(7;2;3)$ và $C(-20;5;-11)$. Tọa độ trọng tâm $G$ của tam giác $ABC$ là

Trong không gian cho hai điểm $M(2;-1;3)$ và $N(2;1;4)$. Khoảng cách $MN$ bằng

Cho vector $\overrightarrow{u}=(-2;3;-1)$. Côsin của góc tạo bởi vectơ $\overrightarrow{u}$ với vectơ đơn vị $\overrightarrow{j}$ của trục $Oy$ bằng

Phương trình mặt cầu có tâm $A(3;1;-1)$ và tiếp xúc với mặt phẳng $zOx$ là

Phương trình mặt cầu có tâm là $A(3;0;2)$ và đi qua gốc tọa độ là:

Trong không gian $Oxyz$ cho hai điểm $A(5;2;5)$ và $B(2;3;1)$. Tọa độ điểm $A'$ đối xứng với $A$ qua $B$ là

Cho hình bình hành $ABCD$, biết tọa độ ba điểm $A(1;-2;1)$, $B(4;-5;3)$ và $C(6;-2;6)$. Tọa độ đỉnh $D$ là

Trong không gian $Oxyz$ cho hai điểm $A(0;-2:0)$ và $B(-1;0:-3)$. Tọa độ điểm $C\in Ox$ sao cho $AC \perp AB$ là

Phương trình mặt cầu có tâm là $A(2;0;-1)$ và đi qua điểm $B(-2;1;0)$ là: