Báo cáo học liệu
Mua học liệu
Mua học liệu:
-
Số dư ví của bạn: 0 coin - 0 Xu
-
Nếu mua học liệu này bạn sẽ bị trừ: 2 coin\Xu
Để nhận Coin\Xu, bạn có thể:

Hai tam giác đồng dạng SVIP
1. ĐỊNH NGHĨA TAM GIÁC ĐỒNG DẠNG
Định nghĩa

Tam giác $ABC$ gọi là đồng dạng với tam giác $DEF$ nếu:
$\widehat A = \widehat D$; $\widehat B = \widehat E$; $\widehat C = \widehat F$;
$\dfrac{AB}{DE} = \dfrac{AC}{DF} = \dfrac{BC}{EF}$.
Kí hiệu
$\Delta ABC \backsim \Delta DEF$ (viết đúng thứ tự cặp đỉnh tương ứng).
Tỉ số đồng dạng
Với $\dfrac{AB}{DE} = \dfrac{AB}{DE} = \dfrac{AB}{DE} = k$ thì $k$ là tỉ số đồng dạng của $\Delta ABC$ và $\Delta DEF$.
Ví dụ 1.
Chứng minh hai tam giác $ABC$ và $MNP$ đồng dạng.
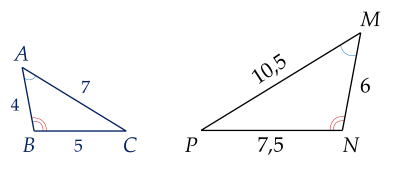
Lời giải
Xét tam giác $ABC$ và tam giác $MNP$:
$\widehat A = \widehat M$; $\widehat B = \widehat N$; $\widehat C = \widehat P$;
$\dfrac{AB}{MN} = \dfrac{BC}{NP} = \dfrac{AC}{MP}$.
Do đó, $\Delta ABC \backsim \Delta DEF$.
Nhận xét
+ Nếu $A'B'C'$ với tỉ số đồng dạng $k$ thì $\Delta A'B'C' \backsim \Delta ABC$ với tỉ số $\dfrac1k$.
+ Hai tam giác bằng nhau thì đồng dạng với nhau theo tỉ số đồng dạng $k = 1$. Đặc biệt, mọi tam giác đồng dạng với chính nó.
+ Nếu $\Delta ABC \backsim \Delta A'B'C'$ với tỉ số đồng dạng $k$ và $\Delta A'B'C' \backsim \Delta A''B''C''$ với tỉ số đồng dạng $h$ thì $\Delta ABC \backsim \Delta A''B''C''$ với tỉ số đồng dạng: $m = k . h$.
Câu hỏi:
@202305450483@
2. ĐỊNH LÍ VỀ TAM GIÁC ĐỒNG DẠNG
Định lí
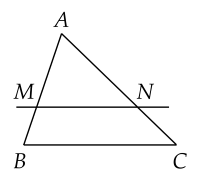
Nếu một đường thẳng cắt hai cạnh của một tam giác và song song với cạnh còn lại thì nó tạo thành một tam giác với đồng dạng với tam giác đã cho.
Chú ý
Định lí trên vẫn đúng nếu đường thẳng cắt phần kéo dài của hai cạnh tam giác. Chẳng hạn:
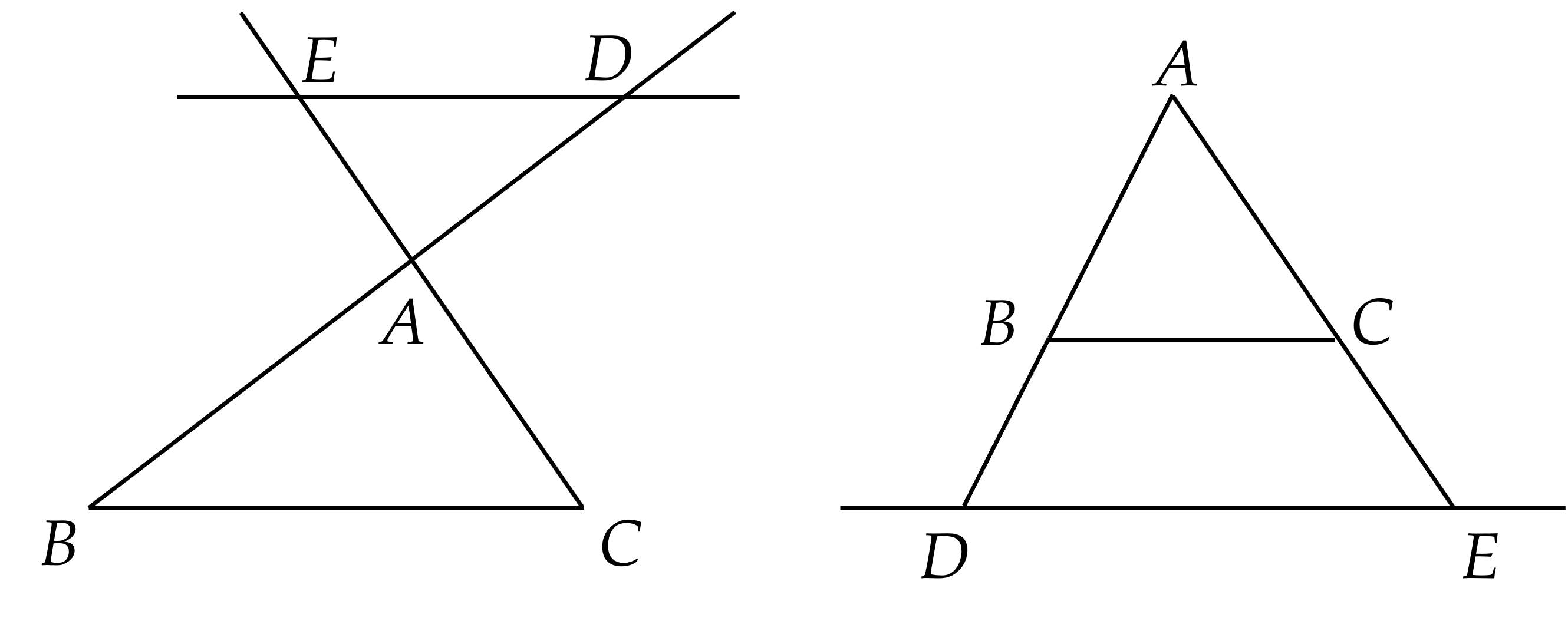
Ví dụ 2.
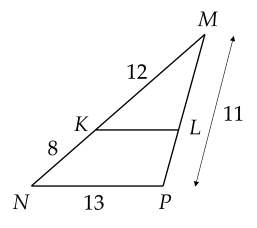
Cho hình vẽ, biết $KL$ // $NP$. Tính độ dài cạnh $KL$ và $ML$.
Lời giải
Xét tam giác $\Delta MNP$ có $KL$ // $NP$.
Suy ra $\Delta MKL \backsim \Delta MNP$.
Do đó, $\dfrac{KL}{NP}=\dfrac{ML}{MP}=\dfrac{MK}{MN}=\dfrac{12}{8+12}=\dfrac{3}{5}$
Vậy
$\dfrac{KL}{NP}=\dfrac{3}{5}$.
Suy ra $KL=\dfrac{3}{5} . NP=\dfrac{3}{5} . 13=\dfrac{39}{5}$
$\dfrac{M L}{M P}=\dfrac{3}{5}$.
Suy ra $M L=\dfrac{3}{5} . M P=\dfrac{3}{5} . 11=\dfrac{33}{5}$.
Câu hỏi:
@202305521308@
Bạn có thể đăng câu hỏi về bài học này ở đây
