Hai tam giác bằng nhau. Trường hợp bằng nhau thứ nhất SVIP

1. Hai tam giác bằng nhau

Khái niệm:

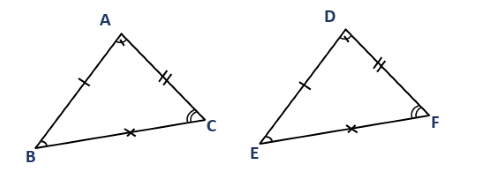
Hai tam giác \(ABC\) và \(DEF\) bằng nhau nếu chúng có các cạnh tương ứng bằng nhau và các góc tương ứng bằng nhau, nghĩa là:

$\left\{\begin{aligned}&AB=DE, \, AC=DF, \, BC=EF\\&\widehat{A}=\widehat{D}, \, \widehat{B}=\widehat{E}, \, \widehat{C}=\widehat{F}\\ \end{aligned}\right.$

Khi đó ta viết \(\Delta ABC=\Delta DEF\).

Ví dụ 1:

Cho tam giác \(ABC\) và \(MNP\) có $AB=MN, \, AC=MP, \, BC=NP$ và $\widehat{A}=\widehat{M}, \, \widehat{B}=\widehat{N}$. Chứng minh rằng:

a, $\widehat{C}=\widehat{P}$

b, \(\Delta ABC=\Delta MNP\)

Lời giải

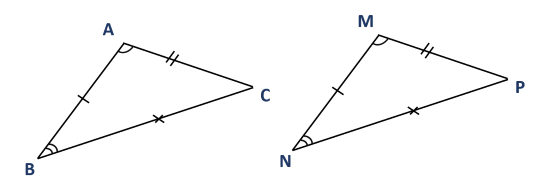
a, Trong tam giác \(ABC\) có:

\(\widehat{A}+\widehat{B}+\widehat{C}=180^o\) (định lí tổng ba góc trong một tam giác)

Suy ra \(\widehat{C}=180^o-\widehat{A}-\widehat{B}\)    (1)

Trong tam giác \(MNP\) có:

\(\widehat{M}+\widehat{N}+\widehat{P}=180^o\) (định lí tổng ba góc trong một tam giác)

Suy ra \(\widehat{P}=180^o-\widehat{M}-\widehat{N}\)    (2)

Theo đề bài ta có $\widehat{A}=\widehat{M}, \, \widehat{B}=\widehat{N}$ và kết hợp với (1), (2) ta được: \(\widehat{C}=\widehat{P}\)

b, Xét hai tam giác \(ABC\) và \(MNP\) có:

$AB=MN, \, AC=MP, \, BC=NP$ (giả thiết)

$\widehat{A}=\widehat{M}, \, \widehat{B}=\widehat{N}$ (giả thiết), \(\widehat{C}=\widehat{P}\) (chứng minh trên)

Các cặp cạnh và cặp góc tương ứng của hai tam giác bằng nhau.

Vậy \(\Delta ABC=\Delta MNP\)

2. Trường hợp bằng nhau thứ nhất của tam giác: cạnh-cạnh-cạnh (c.c.c)

Định lí:

Nếu ba cạnh của tam giác này bằng ba cạnh của tam giác kia thì hai tam giác đó bằng nhau.

Ví dụ 2:

Chứng minh \(\Delta ABC=\Delta A'B'C'\)

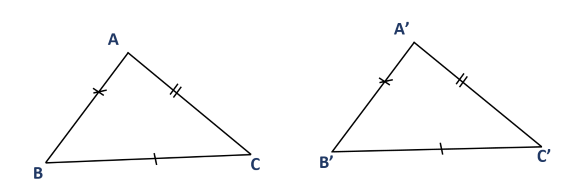
Lời giải

Xét tam giác \(ABC\) và tam giác \(A'B'C'\) có:

\(AB=A'B'\)

\(AC=A'C'\)

\(BC=B'C'\)

Vậy \(\Delta ABC=\Delta A'B'C'\) (c.c.c)

Ví dụ 3:

Cho hình dưới đây biết: $AB=AC, \, BH=HC$. 

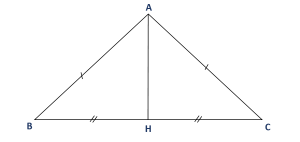
Chứng minh rằng: \(\Delta ABH=\Delta ACH\) 

Lời giải

Xét tam giác \(ABH\) và tam giác \(ACH\) có:

\(AB=AC\) (theo giả thiết)

\(BH=CH\) (theo giả thiết)

\(AH\) là cạnh chung

Vậy \(\Delta ABH=\Delta ACH\) (c.c.c).

@202189710652@