Báo cáo học liệu
Mua học liệu
Mua học liệu:
-
Số dư ví của bạn: 0 coin - 0 Xu
-
Nếu mua học liệu này bạn sẽ bị trừ: 2 coin\Xu
Để nhận Coin\Xu, bạn có thể:

Hai mặt phẳng song song, định lí Thales trong không gian SVIP
1. Hai mặt phẳng song song
🔹Hai mặt phẳng $(\alpha)$ và $(\beta)$ được gọi là song song với nhau nếu chúng không có điểm chung, kí hiệu $(\alpha)$ // $(\beta)$ hay $(\beta)$ // $(\alpha)$.
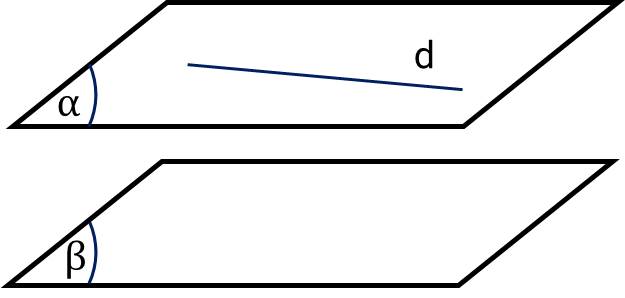
Nhận xét. Nếu hai mặt phẳng $(\alpha)$ và $(\beta)$ song song với nhau và đường thẳng $d$ nằm trong $(\alpha)$ thì $d$ và $(\beta)$ không có điểm chung, tức là $d$ song song với $(\beta)$.
Như vậy, nếu một đường thẳng nằm trong một trong hai mặt phẳng song song thì đường thẳng đó song song với mặt phẳng còn lại.
2. Điều kiện và tính chất của hai mặt phẳng song song
🔹 Nếu mặt phẳng $(\alpha)$ chứa hai đường thẳng cắt nhau và hai đường thẳng này song song với mặt phẳng $(\beta)$ thì $(\alpha)$ và $(\beta)$ song song với nhau.
🔹 Qua một điểm nằm ngoài một mặt phẳng cho trước có một và chỉ một mặt phẳng song song với mặt phẳng đã cho.
🔹 Cho hai mặt phẳng song song. Nếu một mặt phẳng cắt mặt phẳng này thì cũng cắt mặt phẳng kia và hai giao tuyến song song.
3. Định lí Thales (Ta - lét) trong không gian
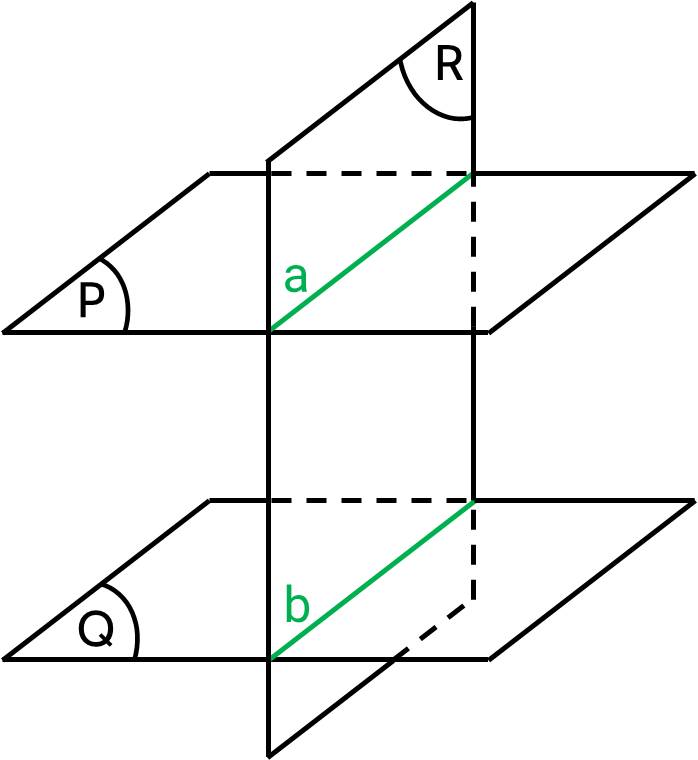
Ba mặt phẳng đôi một song song chắn trên hai cát tuyến phân biệt bất kì những đoạn thẳng tương ứng tỉ lệ.

Trong hình vẽ, ta có $\dfrac{AB}{A'B'}=\dfrac{BC}{B'C'}=\dfrac{AC}{A'C'}$.
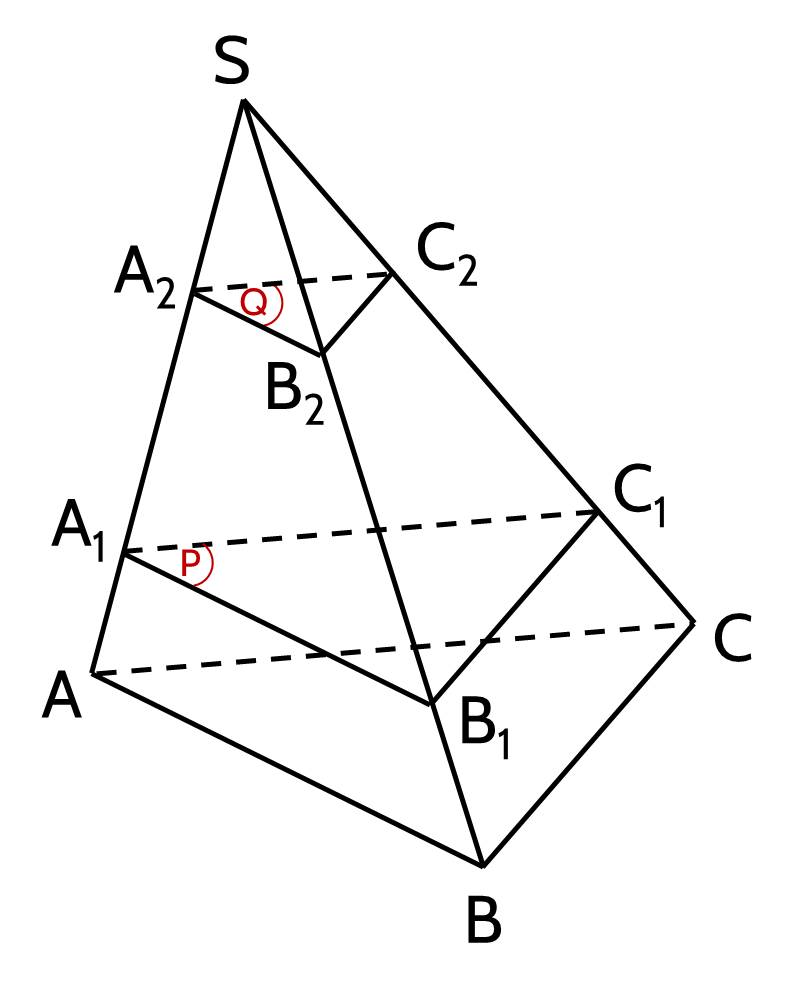
Ví dụ 4: Cho hình tứ diện $S A B C$. Trên cạnh $S A$ lấy các điểm $A_1, A_2$ sao cho $A_2 A_1=2 A_1 A$. Gọi $(P)$ và $(Q)$ là hai mặt phẳng song song với mặt phẳng $(A B C)$ và lần lượt đí qua $A_1, A_2$. Mặt phẳng $(P)$ cắt các cạnh $S B, S C$ lần lượt tại $B_1, C_1$. Mặt phẳng $(Q)$ cắt các cạnh $S B, S C$ lần lượt tại $B_2, C_2$ (xem hình vẽ). Chứng minh $B_2 B_1=2 B_1 B$ và $C_2 C_1=2 C_1 C$.
Giải
Áp dụng định lí Thalès cho ba mặt phẳng đôi một song song $(P),(Q),(A B C)$ và hai cát tuyến $S A, S B$, ta có $\dfrac{A_2 A_1}{A_1 A}=\dfrac{B_2 B_1}{B_1 B}$. Vì $A_2 A_1=2 A_1 A$ nên $B_2 B_1=2 B_1 B$.
Tương tự với hai cát tuyến $S A,\, S C$ suy ra $C_2 C_1=2 C_1 C$.
Bạn có thể đăng câu hỏi về bài học này ở đây
