Hai đường thẳng song song SVIP

1. DẤU HIỆU NHẬN BIẾT HAI ĐƯỜNG THẲNG SONG SONG

a) Hai góc so le trong và hai góc đồng vị

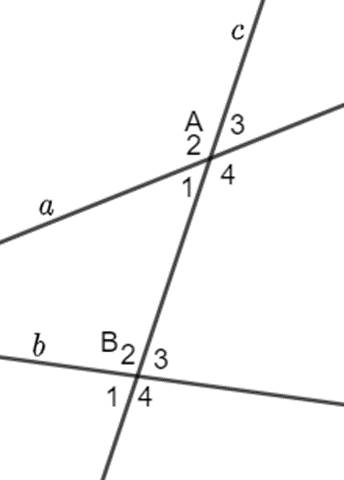
Hai góc $\widehat A_1$ và $\widehat B_3$ (tương tự $\widehat A_4$ và $\widehat B_2$) gọi là hai góc so le trong.

Hai góc $\widehat A_1$ và $\widehat B_1$ (tương tự $\widehat A_2$ và $\widehat B_2$; $\widehat A_3$ và $\widehat B_3$; $\widehat A_4$ và $\widehat B_4$) gọi là hai góc đồng vị.

Ta thừa nhận tính chất sau: 

Nếu đường thẳng $c$ cắt hai đường thẳng $a$, $b$ và trong các góc tạo thành có một cặp góc so le trong bằng nhau (hoặc một cặp góc đồng vị bằng nhau) thì $a$ và $b$ song song với nhau.

Chú ý: Hai đường thẳng phân biệt cùng vuông góc với một đường thẳng thứ ba thì chúng song song với nhau.

b) Cách vẽ hai đường thẳng song song

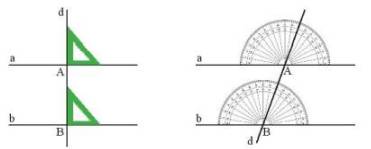
1. Cách 1: Vẽ a, b cùng vuông góc với một đường thẳng d.
2. Cách 2: Vẽ a, b cùng tạo với đường thẳng d những góc so le trong hoặc đồng vị bằng nhau.

2. TIÊN ĐỀ EUCLID VỀ ĐƯỜNG THẲNG SONG SONG

Tiên đề Euclid: 

Qua một điểm nằm ngoài một đường thẳng chỉ có một đường thẳng song song với đường thẳng đó.

Ví dụ: Cho hai đường thẳng phân biệt $a$ và $b$ cùng song song với đường thẳng $c$. Hãy giải thích tại sao $a$ // $b$.

Giải

Ta có $a$ // $c$ và $b$ // $c$ ($a$ khác $b$). Nếu $a$ có điểm chung M với $b$ thì qua điểm M ta vẽ được hai đường thẳng là $a$ và $b$ cùng song song với $c$, điều này trái với tiên đề Euclid. Vậy $a$ không có điểm chung với $b$, suy ra $a$ // $b$.

Chú ý: Hai đường thẳng phân biệt cùng song song với một đường thẳng thứ ba thì song song với nhau.

3. TÍNH CHẤT CỦA HAI ĐƯỜNG THẲNG SONG SONG

Từ tiên đề Euclid, ta có các tính chất sau: 

Nếu một đường thẳng cắt hai đường thẳng song song thì:

a) Hai góc so le trong bằng nhau;

b) Hai góc đồng vị bằng nhau.

Chú ý: Một đường thẳng vuông góc với một trong hai đường thẳng song song thì nó cũng vuông góc với đường thẳng còn lại.