Bài học cùng chủ đề
Báo cáo học liệu
Mua học liệu
Mua học liệu:
-
Số dư ví của bạn: 0 coin - 0 Xu
-
Nếu mua học liệu này bạn sẽ bị trừ: 2 coin\Xu
Để nhận Coin\Xu, bạn có thể:
CHÚC MỪNG
Bạn đã nhận được sao học tập

Chú ý:
Thành tích của bạn sẽ được cập nhật trên bảng xếp hạng sau 1 giờ!
Giới thiệu tứ giác SVIP

Nếu video không chạy trên Zalo, bạn vui lòng Click vào đây để xem hướng dẫn
Lưu ý: Ở điểm dừng, nếu không thấy nút nộp bài, bạn hãy kéo thanh trượt xuống dưới.
Bạn phải xem đến hết Video thì mới được lưu thời gian xem.
Để đảm bảo tốc độ truyền video, OLM lưu trữ video trên youtube. Do vậy phụ huynh tạm thời không chặn youtube để con có thể xem được bài giảng.
Nội dung này là Video có điểm dừng: Xem video kết hợp với trả lời câu hỏi.
Nếu câu hỏi nào bị trả lời sai, bạn sẽ phải trả lời lại dạng bài đó đến khi nào đúng mới qua được điểm dừng.
Bạn không được phép tua video qua một điểm dừng chưa hoàn thành.
Dữ liệu luyện tập chỉ được lưu khi bạn qua mỗi điểm dừng.
Lưu ý: Ở điểm dừng, nếu không thấy nút nộp bài, bạn hãy kéo thanh trượt xuống dưới.
Bạn phải xem đến hết Video thì mới được lưu thời gian xem.
Để đảm bảo tốc độ truyền video, OLM lưu trữ video trên youtube. Do vậy phụ huynh tạm thời không chặn youtube để con có thể xem được bài giảng.
Nội dung này là Video có điểm dừng: Xem video kết hợp với trả lời câu hỏi.
Nếu câu hỏi nào bị trả lời sai, bạn sẽ phải trả lời lại dạng bài đó đến khi nào đúng mới qua được điểm dừng.
Bạn không được phép tua video qua một điểm dừng chưa hoàn thành.
Dữ liệu luyện tập chỉ được lưu khi bạn qua mỗi điểm dừng.
Theo dõi OLM miễn phí trên Youtube và Facebook:
https://youtu.be/GA7ikM3LZNs
Đây là bản xem trước câu hỏi trong video.
Hãy
đăng nhập
hoặc
đăng ký
và xác thực tài khoản để trải nghiệm học không giới hạn!
Câu 1 (1đ):
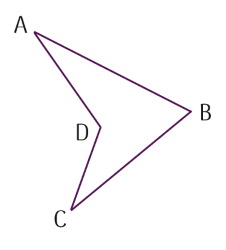
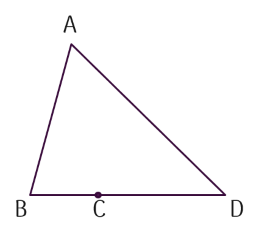
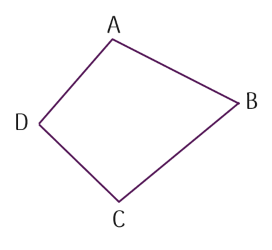
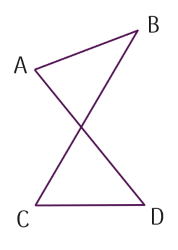
Những hình nào sau đây có hai đoạn thẳng bất kì nào cũng không cùng nằm trên một đường thẳng?



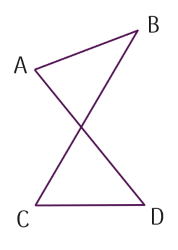
Câu 2 (1đ):
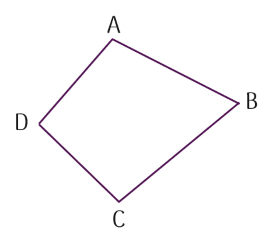
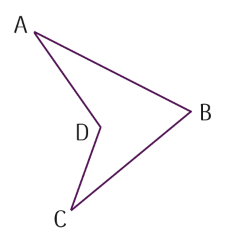
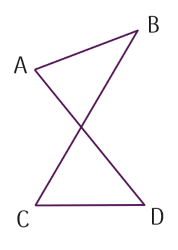
Chọn một cạnh bất kì của mỗi tứ giác. Tứ giác nào luôn nằm trong một nửa mặt phẳng có bờ là đường thẳng chứa cạnh đã chọn?


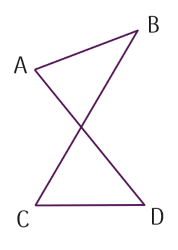
Câu 3 (1đ):
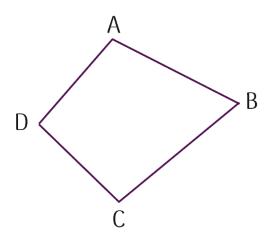
Tứ giác ABCD có cặp đỉnh kề nhau là A và B; B và C;
Câu 4 (1đ):
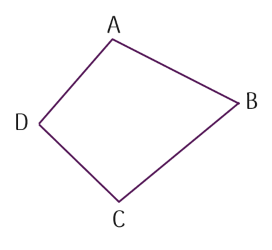
Tứ giác ABCD có hai cặp cạnh đối nhau là AB với CD và
BD với AC.
BC với AD.
BD với AD.
BC với AB.
Câu 5 (1đ):
Cho hình vẽ:
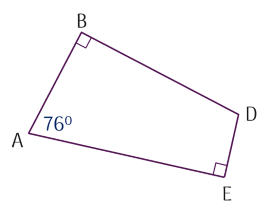
Số đo góc BDE bằng
76∘.
104∘.
106∘.
114∘.
Văn bản dưới đây là được tạo ra tự động từ nhận diện giọng nói trong video nên có thể có lỗi
- Xin
- [âm nhạc]
- chào mừng ghép đã quay trở lại với khóe
- chị newart.vn khi kết thúc tuổi học
- trước khi thay cổ nhắc lại cho các bạn
- về một nội dung liên quan tới hình học
- đó là tổng ba góc trong tam giác nội
- dung đó liên quân trực tiếp từ bài học
- đầu tiên trong chương trình học lớp 8 đó
- là tứ giác và trong bài học tuần này
- thay sẽ giới thiệu qua cho các em về tự
- giác hay nội dung chính ở trong bài học
- ngày hôm nay một thế nào là tứ giác và
- hay là tổng 4 góc trong tứ giác Tuy
- nhiên đây không phải là những nội dung
- mới đâu bởi vì chúng ta đều đã được học
- những kiến thức nên tàng ở cầu lập dưới
- rồi Vậy thì kèm sẽ cùng thầy khởi động
- với câu hỏi đầu tiên thầy cho bộ hình vẽ
- các bạn sẽ xác định cho thấy mỗi hình vẽ
- được tạo thành bởi bao nhiêu đoạn thẳng
- ý với câu này thì chắc chắn là các bạn
- sẽ trả lời được ngay thôi hình đầu tiên
- của bốn gạch tạo bởi bật thẳng hình thứ
- hai là ba hình thứ ba là năm và hình
- cuối cùng là 4 trong đó hình số 2 gồm 3
- cạnh người ta còn gọi là tam giác hình 5
- cạnh còn gọi là ngũ sắc và hai hình đó
- không phải là nội dung mà chúng ta tìm
- hiểu trong bài học ngày hôm nay mà hai
- hình còn lại cùng có bốn cạnh hay nói
- khác chúng được tạo thành từ 4 đoạn
- thẳng Đó là hình ảnh của các tứ giác vậy
- có phải cứ hình nào mà gồm 4 đoạn thẳng
- nối lại với nhau đều là tứ giác hay
- không Chúng ta sẽ đi Tìm câu trả lời
- thông qua có hỏi sau đây cho các hình
- gồm 4 đoạn thẳng là AB BC CD và D cả bố
- hình này đều gồm 4 đoạn thẳng như thế
- vẫn Những hình nào mà thầy chọn ra hai
- đoạn thẳng bất kỳ thì chúng đều không
- cùng nằm trên một đường thẳng
- thì các bạn quan sát và trả lời rất
- chính xác trong hình đầu tiên thầy cô
- chọn đây với PC hay là ad với AB thì
- chúng đều không cùng nằm trên một đường
- thẳng Bởi vì trong bốn điểm A B C D đó
- không có ba điểm nào thẳng hàng cả hình
- thứ 2 và hình thứ ba đều như thế nhưng
- hình cuối cùng các bạn sẽ thấy là
- bc&d quan điểm này thẳng hàng hay nói
- cách khác loại PC và đoạn c d cùng nằm
- trên đường thẳng BD khi đó hình cuối
- cùng của chúng ta không phải là một tứ
- giác mà muốn là tứ giác bên cạnh việc
- gồm 4 đoạn thẳng thì không có hai đoạn
- thẳng bất kỳ nào cùng nằm trên một đường
- thẳng ta có khái niệm về tứ giác như sau
- tứ giác ABCD là hình gồm 4 đoạn thẳng AB
- BC CD d a trong đó bất kì hai đoạn thẳng
- nào cũng không cùng nằm trên 1 A và trên
- đây Các bạn thấy được ba ví dụ về các
- thử xác
- trong các tứ giác đó
- ABCD được gọi là các đỉnh và AB BC CD 3
- 4 đoạn thẳng này chính là các cạnh của
- tứ giác Tuy nhiên trong chương trình lớp
- 8 tới chúng ta không đi tìm hiểu tất cả
- các tứ giác đó mà tập trung vào một loại
- đó là loại nào thì các bạn tiếp tục trả
- lời cho thành câu hỏi sau đây các bạn sẽ
- quan sát thật kỹ vào bài giảng trên bà
- tứ giác trên cho thể biết nếu như thì
- chọn một cạnh bất kỳ của một thứ rác
- những tứ giác nào luôn nằm trong một nửa
- mặt phẳng có bờ là đường thẳng mà thầy
- đã chọn
- thế Quan sát hình đổi tiền nhất tứ giác
- ABCD này thể chọn cạnh ab ad các bạn có
- thể chọn cạnh khác cũng được khi đó
- đường thẳng chứa cạnh AB chính là đường
- thẳng này thì ta sẽ thấy cả ê ê ABCD nằm
- trong một nửa mặt phẳng với bờ là đường
- thẳng AB chính là nửa mặt phẳng này khi
- đó hình thứ nhất thỏa mãn yêu cầu của
- chúng ta
- những hình số 2 thầy chọn một cạnh ví dụ
- cạnh AD đi và đường thẳng chứa cạnh AB
- là đường thẳng màu xanh này thì một phần
- của tứ giác nằm ở bên này Phân tứ giác
- còn lại lại nằm ở nửa mặt phẳng còn lại
- có bờ là đường thẳng chúng ta vừa kẻ cho
- nên hình số 2 là một hình không thỏa mãn
- vậy hình cuối cùng có thỏa mãn hay không
- Ví dụ đây thể chọn đường thẳng chứa cạnh
- AD thì tứ giác của chúng ta cũng có một
- phần nằm ở nửa mặt phẳng này một phần
- nằm ở nửa mặt phẳng còn lại có bờ là
- đường thẳng vừa vẽ nên hình cuối cùng
- cũng không thỏa mãn yêu cầu
- ạ và chúng ta sẽ quan tâm vào hình thỏa
- mãn hai yêu cầu trên tứ sắc ABCD này
- được gọi là tứ giác lồi và Đó cũng là
- đối tượng mà chúng ta sẽ tìm hiểu trong
- chương trình lớp 8 cũng như phần hình
- học sau này
- ở bên cạnh khái niệm tứ giác ta có thêm
- khái niệm tứ giác lồi tứ giác lồi là tứ
- giác luôn nằm trong một nửa mặt phẳng có
- bờ là đường thẳng chứa cạnh bất kỳ của
- tứ giác các bạn có thể lấy cạnh AB BC CD
- hay đĩa thì tứ giác này luôn nằm trong
- một nửa mặt phẳng có bờ là đường thẳng
- chứa cạnh Vừa chọn cho nên từ bây giờ
- túi xách mà người ta không nói gì thêm
- thì ta coi đó là tứ giác lồi và chủ yếu
- các bạn làm việc với tứ giác lồi nhất
- vậy tứ giác lồi ABCD này có những đặc
- điểm gì thì cả bạn sẽ cùng thấy tìm hiểu
- ở phần tiếp theo đây là một nội dung mà
- chúng ta cũng đã tìm hiểu rồi tứ giác
- ABCD thì bên cạnh các đỉnh các cách ta
- đã nhắc đến ở phần trước con có hai mình
- về nhau ví dụ trên hình có A B là hai
- định kề nhau chung chính là hai đầu mút
- của một đoạn thẳng tạo nên tự giác đó
- Vậy tương tự ta có ở đây cũng là hai
- đỉnh kè nhau phá
- có phải chính xác rồi c d đ đó là hai
- cặp đỉnh kỳ nhau còn lại Cùng với đó là
- hai đỉnh đối nhau Ví dụ như a&c vị trí
- của chúng như thế này như là chúng không
- cùng nằm trên một cách Vậy tương tự ta
- sẽ có hai mình đối nhau tiếp theo sẽ là
- B phải D sau đỉnh thì ta cạnh hai cạnh
- kề nhau và hai cạnh đối nhau ví dụ hai
- cạnh kề nhau sẽ là ab và bc A B và B C
- cùng chung nhau một đỉnh tương tự như
- thế BC CD
- cd-r và iap ta có 4 Cặp cạnh kề nhau em
- còn hai cặp cạnh đối nhau là hai cặp
- cạnh mà chúng không có định chung nào cả
- ví dụ như a b thì CD là hai cặp cạnh đối
- nhau
- vậy trên tứ giác này còn cặp cạnh đối
- nhau nào khác hay không
- chính xác ID và PC chỉ là cặp cạnh đối
- nhau còn lại và từ hai mình đối nhau
- Chúng ta có các đường chéo đường chéo
- chính là đoạn thẳng Nối hai đỉnh đối
- nhau lại Nối A với c ta được đường chéo
- AC
- Nội bay với d ta được đường chéo BD và
- một tứ giác thì có hai đường chéo các
- bạn nhất ứng với mỗi đình ta cổ các góc
- và có bún góc là góc A góc B góc C góc D
- thì các bạn sẽ hiểu học ở đây chính là
- góc dab nhá góc B là góc ABC góc B C D
- và góc C D a độ là bốn góc của tứ giác
- trên và hai góc đối nhau sẽ là góc A và
- góc C là hai góc ứng với hai đỉnh đối
- nhau vậy thì hai góc đối nhau còn lại
- chính lá góc B và góc D lại chú ý vào
- hình vẽ của tứ giác ABCD thấy có các
- điểm M N P Q như trên hình thì nằm hoàn
- toàn bên trong tứ giác ABCD các gọi đó
- là các điểm nằm trong tứ giác hay gọi
- tắt là điểm trong của tứ giác chính là
- điểm M và p tương tự ta có các điểm nằm
- ngoài tứ giác chính là điểm N và điểm
- quy hay còn gọi là điểm ngoài của tứ
- giác
- Ở trên đây là các đặc điểm của tứ giác
- ABCD mà các bạn cần phải nắm được đó là
- nội dung của phần số một phân số 2 liên
- quan trực tiếp tới phần cuối thầy đã có
- một bài toán lại yêu cầu kem tính tổng
- số đo các góc
- và các bạn tìm được tổng số 54 gốc bằng
- 360 độ tổng số đó 4 góc 4 góc đó chính
- là bốn góc của một tứ giác hay như trên
- hình 4 Gấp a abc
- góc C và góc CDA chúng sẽ có tổng bằng
- 360 độ việc chứng minh các bạn có thể
- Xem lại video tuần trước hoặc thầy tóm
- tắt như sau
- khi sử dụng tổng ba góc trong một tam
- giác sách tam giác a b
- thì góc A + góc D1 + góc B1 ở đây bằng
- 180 độ
- từ tương tự với tam giác cdp thì góc C +
- góc D 2 + góc B2 bằng 180° + tất cả các
- góc đó lại thì ta sẽ thu được tổng 4 góc
- này bằng 180° cộng 180 độ và bằng 360 độ
- tổng quát với một tứ giác bất kỳ tay ta
- sẽ có tổng các góc của một tứ giác bằng
- 360 độ đó là định lý mà các bạn cần phải
- nhiều nhá và vận dụng chúng ta sẽ đến
- với câu hỏi sau đây thấy Cho hình vẽ
- Cho tứ giác ABCD E yêu cầu tính số đo
- góc B D E biết Ngọc k = 76 độ
- chính xác rồi kiến thức chúng ta sử dụng
- chính là định lý trên xếp trong tứ giác
- abde thì ta có tổng các góc A + góc B +
- góc D + E bằng 360 độ pháp 3 góc đã biết
- với các ký hiệu như này thì ta sẽ biết
- được góc B bằng góc e cùng bằng 90° cho
- nên góc D cần tính sẽ bằng 360° - tổng
- của 76 đấy 90 này và 90 độ hai góc D
- bằng 104 độ đó là kết quả của câu hỏi
- này cũng là nội dung cuối cùng trong bài
- học tuần này của chúng ta trong bài học
- tuần này thầy đã giới thiệu cho các bạn
- về tứ giác cũng như định lí tổng 4 góc
- của một tứ giác sau đây các bạn sẽ luyện
- tập phần trắc nghiệm khóa làm việc tự
- luận chỉ có lần đầu chấm vn Em cảm ơn
- chị thường rõ của kem hẹn gặp lại các em
- trong các bài học tiếp theo trên còn là
- một ít tiền nhá á
K
Khách
Bạn có thể đăng câu hỏi về bài học này ở đây
Chưa có câu hỏi thảo luận nào về bài giao này
OLMc◯2022
