Giới hạn tại vô cực SVIP

Giới hạn hữu hạn tại vô cực

Lưu ý: Định nghĩa $\lim\limits _{x \rightarrow-\infty} f(x)=L$ được phát biểu hoàn toàn tương tự.

Ví dụ 1: Tính $\underset{x\to -\infty }{\mathop{\text{lim}}}\,\dfrac{{{x}^{2}}+x+1}{2{{x}^{3}}+2x+5}$.

Giải: Do \(x\rightarrow-\infty\) nên cách giải tương tự như tính giới hạn của dãy số.

$\lim\limits_{x \rightarrow-\infty} \dfrac{x^2+x+1}{2 x^3+2 x+5}=\lim\limits_{x \rightarrow-\infty} \dfrac{x^2\left(1+\dfrac{1}{x}+\dfrac{1}{x^2}\right)}{x^3\left(2+\dfrac{2}{x^2}+\dfrac{5}{x^3}\right)}=\lim\limits_{x \rightarrow-\infty} \dfrac{\left(1+\dfrac{1}{x}+\dfrac{1}{x^2}\right)}{x\left(2+\dfrac{2}{x^2}+\dfrac{5}{x^3}\right)}=0$.

Giới hạn vô cực tại vô cực

Lưu ý: Các định nghĩa: $\lim\limits _{x \rightarrow-\infty} f(x)=+\infty, \lim\limits _{x \rightarrow+\infty} f(x)=-\infty, \lim\limits _{x \rightarrow-\infty} f(x)=-\infty$ được phát biểu hoàn toàn tương tự.

Một số giới hạn đặc biệt

🔸$\lim\limits _{x \rightarrow \pm \infty} \dfrac{c}{x^k}=0$ ( $c$ là hằng số, $k$ nguyên dương $)$.

🔸$\lim\limits _{x \rightarrow+\infty} x^k=+\infty$ với $k$ nguyên dương.

🔸$\lim\limits _{x \rightarrow-\infty} x^k=-\infty$ nếu $k$ là số nguyên lẻ; $\lim\limits _{x \rightarrow-\infty} x^k=+\infty$ nếu $k$ là số nguyên chẵn.

Nhận xét: $\lim\limits _{x \rightarrow+\infty} f(x)=+\infty \Leftrightarrow \lim\limits _{x \rightarrow+\infty}[-f(x)]=-\infty$.

Ví dụ 1: Tính $\lim\limits _{x \rightarrow-\infty}\left(3 x^4-2 x^2+1\right)$

Giải

Cách 1: Theo nhận xét trên thì $\lim\limits _{x \rightarrow-\infty}\left(3 x^4-2 x^2+1\right)=+\infty\left(x \rightarrow-\infty, k\right.$ chẵn và $\left.a_k>0\right)$.

Thật vậy, ta có $3 x^4-2 x^2+1=x^4\left(3-\dfrac{2}{x^2}+\dfrac{1}{x^4}\right)$.

Vì $\lim\limits _{x \rightarrow-\infty} x^4=+\infty$ và $\lim\limits _{x \rightarrow \infty}\left(3-\dfrac{2}{x^2}+\dfrac{1}{x^4}\right)=3>0$ nên $\lim\limits _{x \rightarrow-\infty}\left(3 x^4-2 x^2+1\right)=+\infty$.

Nhận xét:

🔹 Giới hạn tại vô cực của hàm đa thức là vô cực, chỉ phụ thuộc vào số hạng chứa lũy thừa bậc cao nhất.

🔹 Giới hạn của hàm đa thức tại $+\infty$ phụ thuộc vào hệ số của lũy thừa bậc cao nhất. (Giống với giới hạn của dãy số dạng đa thức).

🔹 Giới hạn của hàm đa thức tại $-\infty$ phụ thuộc vào bậc và hệ số của lũy thừa bậc cao nhất.

Cách 2:(trắc nghiệm)

Sử dụng MTCT tính giá trị hàm số $f(x)=3 x^4-2 x^2+1$ tại $x=-10^{20}$, ta được kết quả như hình:

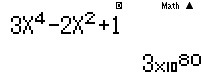
Kết quả là một số dương rất lớn nên có thể suy ra giới hạn bằng $+\infty$.

Ví dụ 3: Cho hàm số $f(x)=\sqrt{x^2-2 x+5}$. Tính $\lim\limits_{x \rightarrow-\infty} f(x)$

Giải

Hàm số $f(x)=\sqrt{x^2-2 x+5}$ xác định trên $\mathbb{R}$.

Có thể giải nhanh như sau : Vì $x^2-2 x+5$ là một hàm đa thức của $x$ nên có giới hạn tại vô cực. Mà $\sqrt{x^2-2 x+5}>0$ với mọi $x$ nên giới hạn của $f(x)=\sqrt{x^2-2 x+5}$ tại $-\infty$ chắc chắn là $+\infty$.

Thật vậy, ta có $\sqrt{x^2-2 x+5}=\sqrt{x^2\left(1-\dfrac{2}{x}+\dfrac{5}{x^2}\right)}=|x| \sqrt{1-\dfrac{2}{x}+\dfrac{5}{x^2}}$.

Vì $\lim\limits_{x \rightarrow-\infty}|x|=+\infty$ và $\lim\limits_{x \rightarrow-\infty} \sqrt{1-\dfrac{2}{x}+\dfrac{5}{x^2}}=1>0$ nên $\lim\limits_{x \rightarrow-\infty} \sqrt{x^2-2 x+5}=+\infty$.

Hoặc ta có thể sử dụng MTCT để tính giá trị của $f(x)$ tại một giá trị âm rất nhỏ của $x$, chẳng hạn tại $x=-10^{20}$ ta được kết quả như hình:

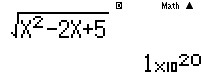
Kết quả này là một số dương rất lớn. (Dễ thấy kết quả hiển thị trên máy tính như trên chỉ là kết quả gần đúng do khả năng tính toán hạn chế của MTCT. Tuy nhiên kết quả đó cũng giúp ta lựa chọn được đáp án chính xác).

Lưu ý:

Ta có $\lim\limits_{x \rightarrow \pm \infty}|x|=+\infty$.

Với $x<0$ ta có $\sqrt{x^2}=|x|=-x$.

Ví dụ 4:

$\lim\limits _{x \rightarrow-\infty}\left(\sqrt{x^2-x}-\sqrt{4 x^2+1}\right)$

Lời giải

Cách 1: Ta có:

$  \begin{aligned}  \sqrt{x^2-x}-\sqrt{4 x^2+1} & \left.=\sqrt{x^2\left(1-\dfrac{1}{x}\right)}-\sqrt{x^2\left(4+\dfrac{1}{x^2}\right.}\right)=|x| \sqrt{1-\dfrac{1}{x}}-|x| \sqrt{4+\dfrac{1}{x^2}} \\  & =|x|\left(\sqrt{1-\dfrac{1}{x}}-\sqrt{4+\dfrac{1}{x^2}}\right)  \end{aligned}  $

Mà $\lim\limits _{x \rightarrow-\infty}|x|=+\infty$ và $\lim\limits _{x \rightarrow \infty}\left(\sqrt{1-\dfrac{1}{x}}-\sqrt{4+\dfrac{1}{x^2}}\right)=1-2=-1<0$.

Vậy $\lim\limits _{x \rightarrow-\infty}\left(\sqrt{x^2-x}-\sqrt{4 x^2+1}\right)=\lim\limits _{x \rightarrow-\infty}\left[|x|\left(\sqrt{1-\dfrac{1}{x}}-\sqrt{4+\dfrac{1}{x^2}}\right)\right]=-\infty$.

Lưu ý: Tại sao ta lại không nhân liên hợp để khử căn thức, lí do như sau:

Vì $\lim\limits _{x \rightarrow-\infty} \sqrt{x^2-x}=+\infty ; \lim\limits _{x \rightarrow-\infty} \sqrt{4 x^2+1}=+\infty$.

Mà hệ số của $x^2$ trong $4 x^2+1$ lớn hơn hệ số của $x^2$ trong $x^2-x$ nên suy ra

$\lim\limits _{x \rightarrow-\infty}\left(\sqrt{x^2-x}-\sqrt{4 x^2+1}\right)=-\infty$.

Cách 2: Sử dụng MTCT tính giá trị hàm số tại $x=-10^{10}$ ta được kết quả như hình:

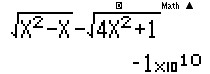
Kết quả rất nhỏ nên có thể kết luận hàm số tiến tới $-\infty $.