Bài học cùng chủ đề
- Giải tam giác
- Một số công thức tính diện tích tam giác
- Giải tam giác và ứng dụng trong thực tế
- Giải tam giác
- Ứng dụng giải tam giác vào thực tế
- Diện tích tam giác
- Tính bán kính đường tròn ngoại tiếp và nội tiếp trong tam giác qua diện tích
- Bài tập tự luận (nâng cao)
- Phiếu bài tập: Diện tích tam giác
Báo cáo học liệu
Mua học liệu
Mua học liệu:
-
Số dư ví của bạn: 0 coin - 0 Xu
-
Nếu mua học liệu này bạn sẽ bị trừ: 0 coin\Xu
Để nhận Coin\Xu, bạn có thể:

Giải tam giác SVIP
I. TÍNH CÁC CẠNH VÀ GÓC CỦA TAM GIÁC DỰA TRÊN MỘT SỐ ĐIỀU KIỆN CHO TRƯỚC
Một tam giác hoàn toàn xác định nếu biết một trong các dữ kiện sau:
- Biết độ dài hai cạnh và độ lớn góc xen giữa hai cạnh đó;
- Biết độ dài ba cạnh;
- Biết độ dài một cạnh và độ lớn hai góc kề với cạnh đó.
Giải tam giác là tính các cạnh và các góc của tam giác dựa trên những dữ kiện cho trước.
Ví dụ. Cho tam giác \(ABC\) có \(\widehat{B}=60^\circ,\widehat{C}=45^\circ,AB=5\). Tính:
a) Số đo góc \(\widehat{A}\)?
b) Tính độ dài cạnh \(AC\) và \(BC\)?
Giải:
a) Áp dụng tổng ba góc trong một tam giác \(180^0\) , ta có: \(\widehat{A}+\widehat{B}+\widehat{C}=180^\circ\)
suy ra \(\widehat{A}=180^\circ-\widehat{B}-\widehat{C}=180^\circ-60^\circ-45^\circ=75^\circ\).
b) Áp dụng định lí sin trong tam giác \(ABC\) ta được:
\(\dfrac{BC}{\sin A}=\dfrac{AC}{\sin B}=\dfrac{AB}{\sin C}\) do đó:
\(AC=\dfrac{AB.\sin B}{\sin C}=\dfrac{5.\sin60^\circ}{\sin45^\circ}\approx6,12\) ;
\(BC=\dfrac{AB.\sin B}{\sin A}=\dfrac{5.\sin60^\circ}{\sin75^\circ}\approx4,48\).
II. DIỆN TÍCH TAM GIÁC
Cho tam giác \(ABC\) có \(BC=a,CA=b,AB=c\). Khi đó diện tích \(S\) của tam giác \(ABC\) là:
- \(S=\dfrac{1}{2}bc\sin A=\dfrac{1}{2}ca\sin B=\dfrac{1}{2}ab\sin C.\)
- \(S=\sqrt{p\left(p-a\right)\left(p-b\right)\left(p-c\right)}\) (\(p=\dfrac{a+b+c}{2}\) là nửa chu vi của tam giác)
Chú ý. Trong tam giác \(ABC\), ta kí hiệu:
- \(A,B,C\) là các góc của tam giác tại các đỉnh tương ứng.
- \(a,b,c\) tương ứng là độ dài của các cạnh đối diện với đỉnh \(A,B,C\).
- \(p\) là nửa chu vi.
- \(S\) là diện tích.
- \(R,r\) tương ứng là bán kính đường tròn ngoại tiếp, nội tiếp tam giác.
- \(m_a,m_b,m_c\) là độ dài các đường trung tuyến lần lượt xuất phát từ các đỉnh \(A,B,C\).
Khi đó:
- \(m^2_a=\dfrac{b^2+c^2}{2}-\dfrac{a^2}{4};m^2_b=\dfrac{c^2+a^2}{2}-\dfrac{b^2}{4};m^2_c=\dfrac{a^2+b^2}{2}-\dfrac{c^2}{4}.\)
- \(r=\dfrac{S}{p}\).
- \(R=\dfrac{abc}{4S}\).
III. ÁP DỤNG VÀO BÀI TOÁN THỰC TIỄN
Vận dụng giải tam giác giúp ta giải quyết được rất nhiều bài toán trong thực tế, đặc biệt là trong thiết kế và xây dựng.
Ví dụ. Từ vị trí \(A\) người ta quan sát một cây cao (hình vẽ). Biết \(AH=4\) m, \(HB=20\) m, \(\widehat{BAC}=45^\circ\). Tính chiều cao của cây?
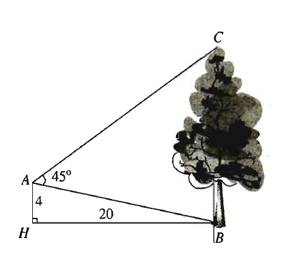
Giải
Trong tam giác vuông \(AHB\) có \(\tan\widehat{ABH}=\dfrac{AH}{BH}=\dfrac{4}{20}=\dfrac{1}{5}\Rightarrow\widehat{ABH}\approx11^\circ19'\)
Ta có \(\widehat{ABH}+\widehat{ABC}=90^\circ\Rightarrow\widehat{ABC}=90^\circ-\widehat{ABH}\approx90^\circ-11^\circ19'\approx78^\circ41'\)
suy ra \(\widehat{ACB}=180^\circ-\left(\widehat{ABC}+\widehat{BAC}\right)\approx56^\circ19'\).
Áp dụng định lí sin cho tam giác \(ABC\) ta được:
\(\dfrac{BC}{\sin\widehat{BAC}}=\dfrac{AB}{\sin\widehat{ACB}}\Rightarrow BC=\dfrac{AB.\sin\widehat{BAC}}{\sin\widehat{ACB}}\approx17\) m.
Vậy chiều cao của cây là \(17\) m.
Bạn có thể đăng câu hỏi về bài học này ở đây
