Đường tròn, sự xác định đường tròn SVIP

Hướng dẫn giải:

a) Nối F và E với D. Vì FD và ED là các đường trung tuyến ứng với cạnh huyền BC của các tam giác vuông BFC và CEB nên: DB = DF = DE = DC. Do đó, bốn điểm B, F, E, C nằm trên đường tròn $\left(D;\frac{BC}{2}\ \right)$.

b) Tam giác ABC cân tại A nên đường trung tuyến AD cũng là đường cao, do đó AD đi qua H và $\widehat{ADC}={90}^\circ$. Gọi I là trung điểm của HC thì DI và EI là các đường trung tuyến ứng với cạnh huyền HC của các tam giác vuông HDC và HEC. Ta có ID = IH = IE = IC nên bốn điểm D, H, E, C nằm trên đường tròn $\left(I\ ;\frac{HC}{2}\right)$.

c) Gọi K là trung điểm của AC. Tương tự câu a) ta có bốn điểm A, F, D, C nằm trên đường tròn $\left(K;\frac{AC}{2}\right)$.

Hướng dẫn giải:

a) Chứng minh được BF = DH $\Rightarrow$ BFDH là hình bình hành (vì BF // DH). Do đó O thuộc FH (vì O phải là giao điểm của hai đường chéo).

b) Dễ thấy $\Delta BEF=\Delta CFG$ (cgv – cgv) nên EF = FG.

Tương tự, FG = GH, GH = HE $\Rightarrow$ EF = FG = GH = HE. Suy ra EFGH là hình vuông.

Tương tự phần a) ta chứng minh được O thuộc EG. Từ đó, O là giao điểm hai đường chéo của hình vuông EFGH nên O cách đều E, F, G, H.

c) $BE=BC .\cot{{60}^\circ}=\frac{6\sqrt3}{3}=2\sqrt3$.

Hướng dẫn giải:

Do \(\widehat{ABC}=90^o\), suy ra AC là đường kính nên A, O, C thẳng hàng và O là trung điểm AC.
Do ​\(\widehat{ABD}=90^o\)​, suy ra AD là đường kính nên A, O', D thẳng hàng và O là trung điểm AD..

Xét tam giác ACD, có AO = OC, AO= OD nên OO' là đường trung bình của tam giác ACD.

Vậy nên \(OO'=\dfrac{1}{2}CD\).

Hướng dẫn giải:

a) Ta thấy: OB = OC = R; DB = DC = R.

Vậy nên tứ giác OBDC là hình thoi.
b) Tam giác OBD và tam giác OCD đều là tam giác đều, suy ra:
 \(\widehat{OBD}=\widehat{DCO}=\widehat{BOD}=\widehat{BDO}=\widehat{DOC}=\widehat{ODC}=60^o\).
Tứ giác OBDC là hình thoi nên BC là đường phân giác của góc DBO.
Vì vậy \(\widehat{OBC}=\widehat{CBD}=30^o\).
Có \(\widehat{ABD}=90^o\) và \(\widehat{ADB}=60^o\).
Suy ra \(\widehat{OAB}=\widehat{DAB}=180^o-90^o-60^o=30^o\).
c) Tương tự ta cũng có \(\widehat{CAD}=30^o\).
\(\widehat{BAC}=\widehat{BAD}+\widehat{CAD}=30^o+30^o=60^o\).
\(\Delta ADB=\Delta ADC\left(g.c.g\right)\) suy ra \(AB=AC\).
Tam giác ABC cân tại A (AB = AC) có \(\widehat{BAC}=60^o\) nên tam giác ABC đều.

Hướng dẫn giải:

a) Kẻ \(OH\perp AC,OK\perp CB\).

Ta có \(AM=BN\) nên \(OH=OK\).
Do đó:
\(\Delta OHC=\Delta OKC\) (Cạnh huyền - cạnh góc vuông)

\(\Rightarrow\widehat{O_1}=\widehat{O_2}\).
\(\Delta OHC=\Delta OKC\) (Cạnh huyền - cạnh góc vuông)

 \(\Rightarrow\widehat{O_3}=\widehat{O_4}\).
Suy ra \(\widehat{O_1}+\widehat{O_3}=\widehat{O_2}+\widehat{O_4}\)  hay \(\widehat{AOC}=\widehat{BOC}\) nên OC là tia phân giác của góc AOB.
b) Tam giác AOB cân tại O có OC là tia phân giác nên OC đồng thời là đường cao. Vậy nên \(OC\perp AB\).

Hướng dẫn giải:

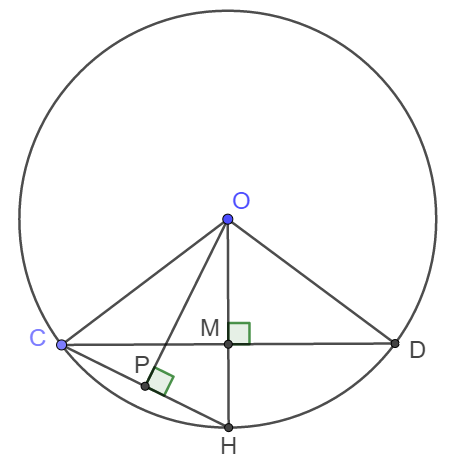
Theo sự liên hệ giữa đường kính và dây cung, ta có H là điểm chính giữa cung CD và M là trung điểm của CD.
Suy ra \(CM=MD=16:2=8\left(cm\right)\).
Áp dụng định lý Pi-ta-go: \(CH=\sqrt{CM^2+HM^2}=\sqrt{8^2+4^2}=4\sqrt{5}\left(cm\right)\).
Kẻ \(OP\perp CH\). Suy ra P là trung điểm của CH.
Vậy thì \(PH=\dfrac{CH}{2}=2\sqrt{5}\left(cm\right)\)
Mà \(\widehat{MCH}=\widehat{POH}\) nên \(sin\widehat{MCH}=sin\widehat{POH}\).
\(\dfrac{PH}{OH}=\dfrac{HM}{CH}\Rightarrow OH=\dfrac{2\sqrt{5}.4\sqrt{5}}{4}=10\left(cm\right)\)
Vậy \(R=10\left(cm\right)\).

Hướng dẫn giải:

a) Qua O, kẻ đường thẳng vuông với với DC và EF, cắt CD và EF lần lượt tại H và K.
Theo tính chất dây cung và đường kính thì H và K lần lượt là trung điểm của DC và EF.
Do M, N lần lượt là trung điểm của OA, OB nên O là trung điểm của MN.
Từ đó ta chứng minh được \(\Delta OHM=\Delta OKN\) (ch - gn).
Suy ra OH = OK vì vậy DC = EF (Liên hệ khoảng cách từ tâm tới dây).

Theo giả thiết thì DC // EF, suy ra tứ giác CDFE là hình bình hành.
Suy ra DE, CF, MN, HK đều cắt nhau tại trung điểm của mỗi đường. 
Mà các đoạn thẳng MN và KH đều có O là trung điểm nên O cũng là trung điểm của DE và CF.
DE và CF lần lượt là đường kính của hình tròn (O) nên \(\widehat{ECD}=90^o\).
Hình bình hành CDFE có một góc vuông nên nó là hình chữ nhật.
b) Có M, N lần lượt là trung điểm của OA và OB.
Suy ra \(OM=MA=ON=NB=\dfrac{R}{2}\).
Do AB và DC tạo với AB một góc nhọn \(30^o\).
Suy ra \(\widehat{AMD}=30^o\Rightarrow\widehat{HMO}=30^o\).
Áp dụng tỉ số lượng giác của góc nhọn, ta có: \(OH=OM.sin30^o=\dfrac{R}{2}.\dfrac{1}{2}=\dfrac{R}{4}\).
Suy ra \(HK=2OH=\dfrac{R}{2}\).
Suy ra \(HK=CE=DF=\dfrac{R}{2}\).
Áp dụng định lý Pi-ta-go ta có:\(DC=\sqrt{DE^2-CE^2}=\sqrt{4R^2-\dfrac{R^2}{4}}=\dfrac{\sqrt{15}}{2}R\).
Diện tích hình chữ nhật CDFE là:  \(CE.DC=\dfrac{R}{2}.\dfrac{\sqrt{15}R}{2}=\dfrac{\sqrt{15}}{4}R^2.\)

Hướng dẫn giải:

Quan sát: Điểm G cách trung điểm M của BC (cố định) một khoảng cố định bằng $\dfrac{m}{3}$.

Kết luận: quỹ tích trọng tâm G của tam giác ABC là đường tròn $(G , \dfrac{m}{3})$ trừ các giao điểm của đường tròn với BC (do G không thể thuộc BC).

Hướng dẫn giải:

Ý tưởng: Cần tìm điểm cố định sao cho C cách điểm đó một khoảng cố định.

Dựng điểm D đối xứng với B qua A, khi đó D là điểm cố định, AM là đường trung bình của tam giác BCD, CD = 2AM = 2m (cố định)

Kết luận: Quỹ tích điểm C là đường tròn (D ; 2m), trừ các giao điểm của nó với đường thẳng AB (khi đó tam giác ABC trở thành đoạn thẳng)