Bài học cùng chủ đề
- Đề và đáp án tuyển sinh vào lớp 10 sở GD&ĐT Nam Định năm 2022 - 2023 (Trắc nghiệm)
- Đề và đáp án tuyển sinh vào lớp 10 sở GD&ĐT Nam Định năm 2022 - 2023 (Tự luận)
- Đề và đáp án tuyển sinh vào lớp 10 thành phố Hà Nội năm 2022 - 2023
- Đề và đáp án tuyển sinh vào lớp 10 thành phố Hồ Chí Minh năm 2022 - 2023
- Đề và đáp án tuyển sinh vào lớp 10 thành phố Đà Nẵng năm 2022 - 2023
- Đề và đáp án tuyển sinh vào lớp 10 tỉnh Vĩnh Phúc năm 2022 - 2023
- Đề thi thử trường THCS & THPT Lương Thế Vinh - Hà Nội 2022-2023
- Đề thi tuyển sinh vào lớp 10 THPT Nghệ An năm 2022-2023
- Đề và đáp án tuyển sinh vào lớp 10 sở GD&ĐT Huế năm 2022 - 2023
- Đề và đáp án tuyển sinh vào lớp 10 sở GD&ĐT Thanh Hóa năm 2022 - 2023
Báo cáo học liệu
Mua học liệu
Mua học liệu:
-
Số dư ví của bạn: 0 coin - 0 Xu
-
Nếu mua học liệu này bạn sẽ bị trừ: 2 coin\Xu
Để nhận Coin\Xu, bạn có thể:

Đề và đáp án tuyển sinh vào lớp 10 thành phố Đà Nẵng năm 2022 - 2023 SVIP
Tính $A=\sqrt{9}+\sqrt{16}+2 \sqrt{2}-\sqrt{8}$.
Hướng dẫn giải:
$\quad A=\sqrt{9}+\sqrt{16}+2 \sqrt{2}-\sqrt{8}$
$A=\sqrt{3^{2}}+\sqrt{4^{2}}+2 \sqrt{2}-\sqrt{2^{2} \cdot 2}$
$ A=3+4+2 \sqrt{2}-2 \sqrt{2}=7$
Rút gọn biểu thức $B=\left(\dfrac{\sqrt{x}}{\sqrt{x}+1}+\dfrac{1}{\sqrt{x}-1}\right): \dfrac{x+1}{x-1}$ với $x \geq 0$ và $x \neq 1$.
Hướng dẫn giải:
Với $x \geq 0$ và $x \neq 1$, ta có:
$ \begin{aligned} B & =\left(\frac{\sqrt{x}}{\sqrt{x}+1}+\frac{1}{\sqrt{x}-1}\right): \frac{x+1}{x-1} \\B & =\left[\frac{\sqrt{x}(\sqrt{x}-1)}{(\sqrt{x}+1)(\sqrt{x}-1)}+\frac{\sqrt{x}+1}{(\sqrt{x}+1)(\sqrt{x}-1)}\right]: \frac{x+1}{x-1} \\B & =\frac{x-\sqrt{x}+\sqrt{x}+1}{(\sqrt{x}+1)(\sqrt{x}-1)} \cdot \frac{x-1}{x+1} \\ B & =\frac{x+1}{x-1} \cdot \frac{x-1}{x+1}=1 \end{aligned} $
Cho hai hàm số $y=-x^{2}$ và $y=2 x-3$.
a) Vẽ đồ thị của các hàm số này trên cùng một mặt phẳng tọa độ.
b) Tìm tọa độ các giao điểm $A$ và $B$ của hai đồ thị đó. Tính diện tích tam giác $O A B$, với $O$ là gốc tọa độ và đơn vị đo trên các trục tọa độ là xentimét.
Hướng dẫn giải:
a) Vẽ đồ thị của các hàm số $y=-x^{2}$ và $y=2 x-3$
* Đồ thị hàm số $y=-x^{2}$ :
Hệ số $a=-1<0$ nên đồ thị hàm số $y=-x^{2}$ là parabol có bề lõm quay xuống dưới.
Bảng giá trị:
| $x$ | -2 | -1 | 0 | 1 | 2 |
| $y=-x^2$ | -4 | -1 | 0 | -1 | -4 |
Suy ra parabol $y=-x^{2}$ đi qua các điểm $(-2 ;-4),(-1 ;-1),(0 ; 0),(1 ;-1),(2 ;-4)$.
* Đồ thị hàm số $y=2 x-3$ :
Bảng giá trị:
| $x$ | 0 | $\dfrac32$ |
| $y = 2x - 3$ | -3 | 0 |
Suy ra đồ thị hàm số $y=2 x-3$ là đường thẳng đi qua hai điểm $(0 ;-3)$ và $\left(\dfrac{3}{2} ; 0\right)$.
* Vẽ đồ thị của các hàm số $y=-x^{2}$ và $y=2 x-3$ :
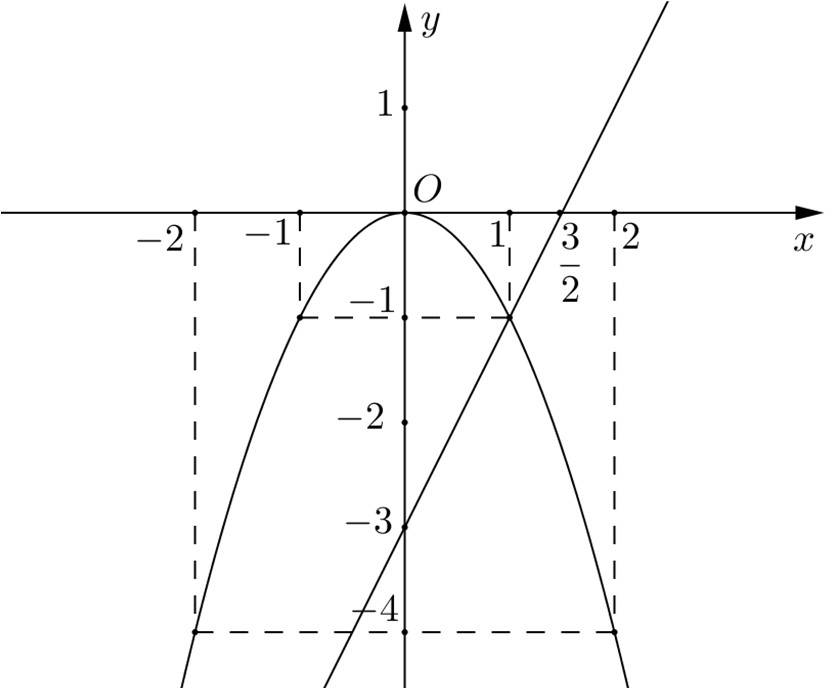
b) Hoành độ giao điểm của đồ thị hàm số $y=-x^{2}$ và $y=2 x-3$ là nghiệm của phương trình: $-x^{2}=2 x-3 \Leftrightarrow-x^{2}-2 x+3=0 \Leftrightarrow x_{1}=1 ; x_{2}=-3$.
Với $x=1 \Rightarrow y=-1 ; x=-3 \Rightarrow y=-9$. Do đó 2 giao điểm là $A(1 ;-1), B(-3 ;-9)$.
Gọi $H, K$ lần lượt là hình chiếu vuông góc của $A, B$ trên trục $O x$.
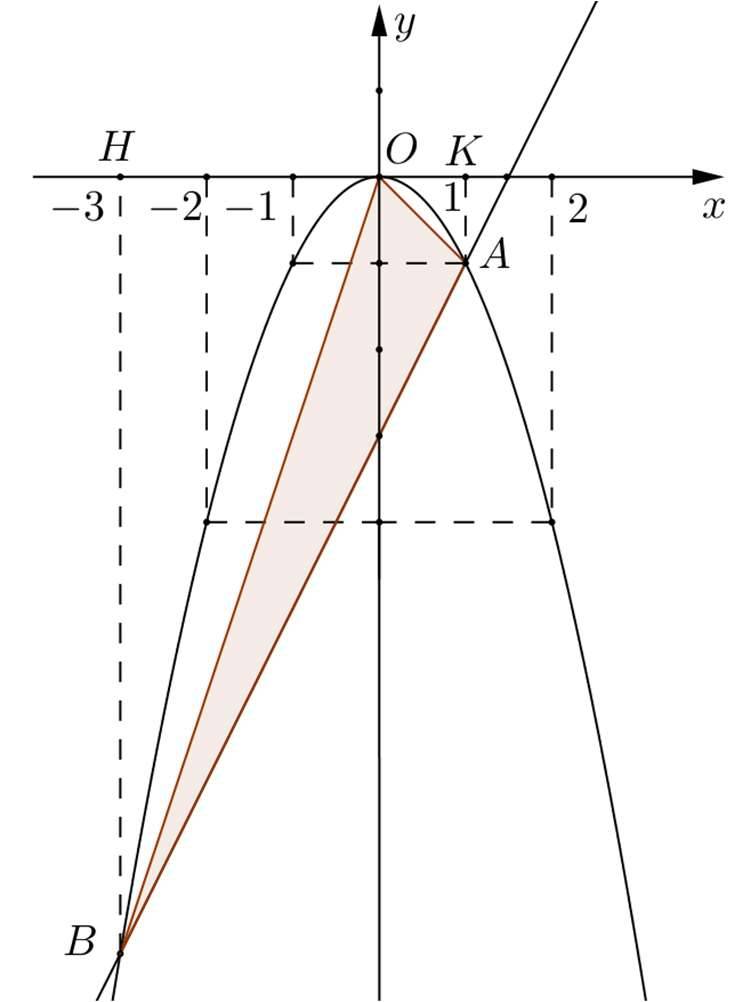
Ta có $S_{\triangle O A B}=S_{A K H B}-S_{\triangle O A K}-S_{\triangle O H B}$
$ \begin{aligned} & S_{\triangle O A B}=\dfrac{A K+H B}{2} \cdot K H-\dfrac{1}{2} A K \cdot O K-\dfrac{1}{2} O H \cdot H B \\ & S_{\triangle O A B}=\dfrac{1+9}{2} \cdot 4-\dfrac{1}{2} \cdot 1 \cdot 1-\dfrac{1}{2} \cdot 3 \cdot 9=6\left(cm^{2}\right) . \end{aligned} $
Vậy diện tích tam giác $O A B$ bằng $6 cm^{2}$.
Giải hệ phương trình $\left\{\begin{array}{l}x-3 y=5 \\ 2 x+3 y=1\end{array}\right.$.
Hướng dẫn giải:
$\left\{\begin{array}{l}x-3 y=5 \\ 2 x+3 y=1\end{array} \Leftrightarrow\left\{\begin{array}{l}3 x=6 \\ x-3 y=5\end{array} \Leftrightarrow\left\{\begin{array}{l}x=2 \\ 2-3 y=5\end{array} \Leftrightarrow\left\{\begin{array}{l}x=2 \\ y=-1\end{array}\right.\right.\right.\right.$.
Vậy hệ phương trình có nghiệm duy nhất: $(x ; y)=(2 ;-1)$.
Một người dự định đi xe máy từ $A$ đến $B$ với vận tốc không đổi. Nhưng sau khi đi được 2 giờ thì xe bị hỏng nên phải dừng lại 20 phút để sửa chữa. Do đó, để kịp đến $B$ đúng thời gian dự định, người đó phải tăng vận tốc thêm $8 km / h$. Tính vận tốc ban đầu của xe máy, biết rằng quãng đường $A B$ dài $160 km$.
Hướng dẫn giải:
Đổi: 20 phút $=\dfrac{1}{3}$ giờ.
Gọi $x(km / h)$ là vận tốc ban đầu của xe máy (điều kiện $x>0$ ).
Thời gian dự định đi từ $A$ đến $B$ là: $\dfrac{160}{x}$ (giờ).
Trong 2 giờ đầu người đó đi được $2 x(km)$. Quãng đường còn lại là $160-2 x(km)$.
Theo bài ra, ta có phương trình:
$ \begin{aligned} & 2+\dfrac{1}{3}+\dfrac{160-2 x}{x+8}=\dfrac{160}{x} \\ & \Leftrightarrow \dfrac{7}{3}+\dfrac{160-2 x}{x+8}=\dfrac{160}{x} \\ & \Leftrightarrow \dfrac{7 x(x+8)}{3 x(x+8)}+\dfrac{3 x(160-2 x)}{3 x(x+8)}=\dfrac{160 \cdot 3 \cdot(x+8)}{3 x(x+8)} \\ & \Rightarrow 7 x^{2}+56 x+480 x-6 x^{2}=480 x+3840 \\ & \Leftrightarrow x^{2}+56 x-3840=0 \end{aligned} $
Ta có: $\Delta^{\prime}=28^{2}-1 .(-3840)=4624>0$
$\Rightarrow$ Phương trình có hai nghiệm phân biệt:
$x_{1}=\dfrac{-28+\sqrt{4624}}{1}=40$ (thỏa mãn) $x_{1}=\dfrac{-28-\sqrt{4624}}{1}=-96($ loại)
Vậy vận tốc ban đầu của xe máy là $40 km / h$.
Cho phương trình $x^{2}-2(m+1) x-m^{2}-3=0\left(^{*}\right)$, với $m$ là tham số.
a. Giải phương trình $\left(^{*}\right)$ khi $m=0$.
b. Tìm tất cả các giá trị của tham số $m$ để phương trình $\left.*^{*}\right)$ có hai nghiệm phân biệt $x_{1}, x_{2}$ thoả mãn $\left(x_{1}+x_{2}-6\right)^{2}\left(x_{2}-2 x_{1}\right)=\left(x_{1} x_{2}+7\right)^{2}\left(x_{1}-2 x_{2}\right)$.
Hướng dẫn giải:
Phương trình: $x^{2}-2(m+1) x-m^{2}-3=0(*)$, với $m$ là tham số
a. Thay $m=0$ vào phương trình $(*)$, ta được: $x^{2}-2 x-3=0(* *)$
Ta có: $a-b+c=1-(-2)+(-3)=0$
$\Rightarrow$ Phương trình $(* *)$ có hai nghiệm là: $x_{1}=-1 ; x_{2}=-\dfrac{(-3)}{1}=3$
Vậy với $m=0$ thì phương trình $(*)$ có hai nghiệm phân biệt là $x_{1}=-1 ; x_{2}=3$.
b. Vì $a . c=-m^{2}-3<0$ với mọi $m \Rightarrow$ phương trình (*) có 2 nghiệm phân biệt $x_{1}, x_{2}$ với mọi $m$.
Hệ thức Vi-et: $\left\{\begin{array}{l}x_{1}+x_{2}=2(m+1) \\ x_{1} \cdot x_{2}=-m^{2}-3\end{array}\right.$
Vì $x_{1} \cdot x_{2}=-m^{2}-3<0$ nên $x_{1}, x_{2}$ trái dấu $\Rightarrow\left(x_{2}-2 x_{1}\right) ;\left(x_{1}-2 x_{2}\right)$ trái dấu.
Mặt khác $\left(x_{1}+x_{2}-6\right)^{2} \geq 0 ;\left(x_{1} x_{2}+7\right)^{2} \geq 0$ với mọi $x_{1}, x_{2}$
Do đó: $\left(x_{1}+x_{2}-6\right)^{2}\left(x_{2}-2 x_{1}\right)=\left(x_{1} x_{2}+7\right)^{2}\left(x_{1}-2 x_{2}\right)$
$\Leftrightarrow\left(x_{1}+x_{2}-6\right)^{2}=\left(x_{1} x_{2}+7\right)^{2}=0$
$\Leftrightarrow(2 m+2-6)^{2}=\left(-m^{2}-3+7\right)^{2}=0$
$\Leftrightarrow(2 m-4)^{2}=\left(m^{2}-4\right)^{2}=0 \Leftrightarrow m=2$
Vậy với $m=2$ thì phương trình $\left(^{*}\right)$ có hai nghiệm phân biệt $x_{1}, x_{2}$ thoả mãn
$\left(x_{1}+x_{2}-6\right)^{2}\left(x_{2}-2 x_{1}\right)=\left(x_{1} x_{2}+7\right)^{2}\left(x_{1}-2 x_{2}\right)$.
Cho tam giác $A B C$ có ba góc nhọn và $A B<A C$. Vẽ các đường cao $A D, B E, C F$ của tam giác đó. Gọi $H$ là giao điểm của các đường cao vừa vẽ.
a) Chứng minh rằng các tứ giác $A E H F$ và $B F E C$ nội tiếp.
b) Gọi $M, N$ lần lượt là trung điểm của các đoạn $A H, B C$. Chứng minh rằng $F M . F C=F N \cdot F A$.
c) Gọi $P, Q$ lần lượt là chân các đường vuông góc kẻ từ $M, N$ đến đường thẳng $D F$. Chứng minh rằng đường tròn đường kính $P Q$ đi qua giao điểm của $F E$ và $M N$.
Hướng dẫn giải:
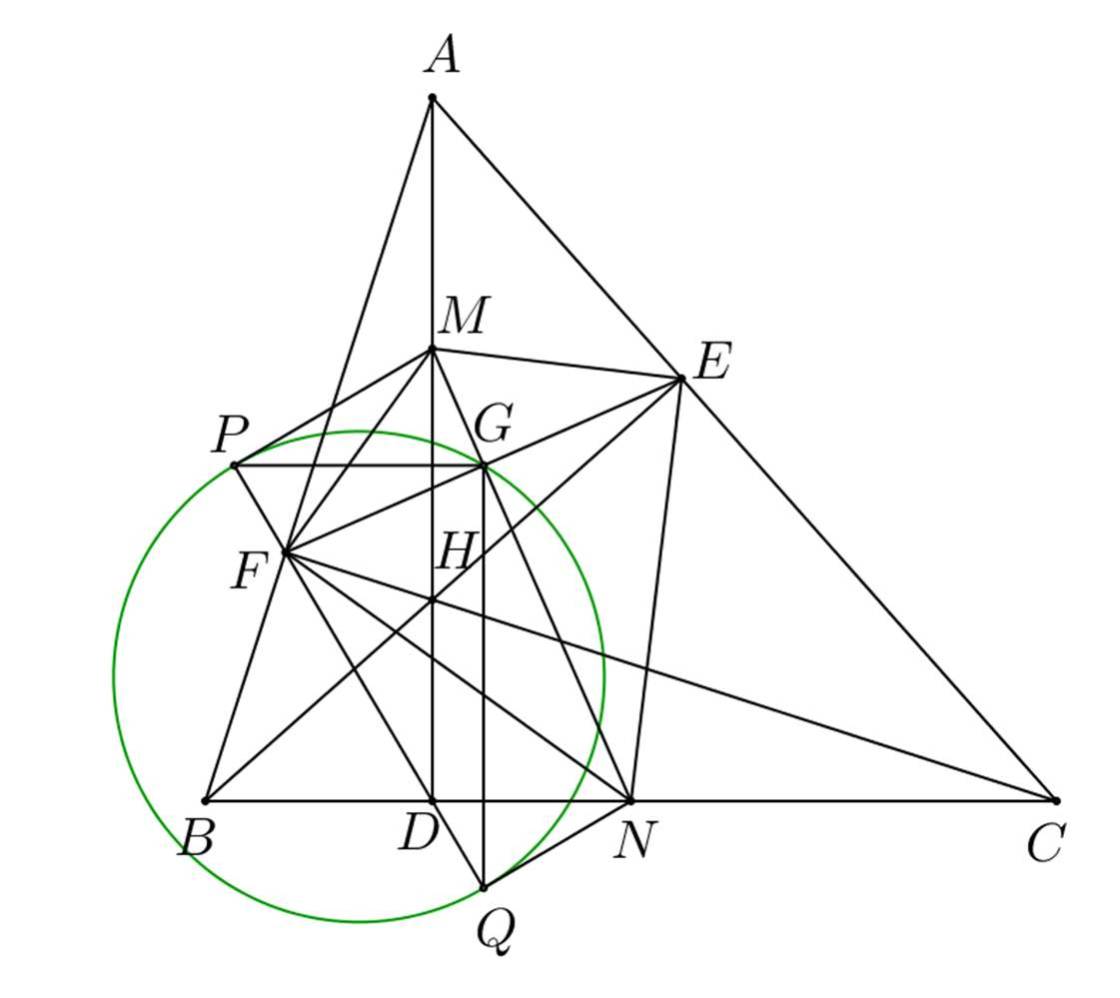
a) Chứng minh rằng các tứ giác $A E H F$ và $B F E C$ nội tiếp
* Xét tứ giác $A E H F$ có $\widehat{A F H}=90^{\circ}$ (do $\left.C F \perp A B\right), \widehat{A E H}=90^{\circ}$ (do $B E \perp A C$ ).
Suy ra $\widehat{A F H}+\widehat{A E H}=180^{\circ}$, mà $\widehat{A F H}$ và $\widehat{A E H}$ ở vị trí đối nhau nên tứ giác $A E H F$ nội tiếp.
* Xét tứ giác $B F E C$ có $\widehat{B F C}=90^{\circ}$ (do $\left.C F \perp A B\right), \widehat{B E C}=90^{\circ}$ (do $B E \perp A C$ ).
Suy ra 2 góc $\widehat{B F C}$ và $\widehat{B E C}$ cùng nhìn đoạn thẳng $B C$ dưới 1 góc bằng nhau nên tứ giác $B F E C$ nội tiếp.
b) Gọi $M, N$ lần lượt là trung điểm của các đoạn $A H, B C$. Chứng minh rằng $F M . F C=F N . F A$.
Tam giác $B F C$ vuông tại $F$ có $F N$ là đường trung tuyến ứng với cạnh huyền $B C$ $\Rightarrow F N=\dfrac{B C}{2}(1)$
Tam giác $B E C$ vuông tại $E$ có $E N$ là đường trung tuyến ứng với cạnh huyền $B C$ $\Rightarrow E N=\dfrac{B C}{2}(2)$
Từ (1) và (2) suy ra $F N=E N(*)$.
Tam giác $A H F$ vuông tại $F$ có $F M$ là đường trung tuyến ứng với cạnh huyền $A H$ $\Rightarrow F M=\dfrac{A H}{2}(3)$
Tam giác $A E H$ vuông tại $E$ có $E M$ là đường trung tuyến ứng với cạnh huyền $A H$ $\Rightarrow E M=\dfrac{A H}{2}(4)$
Từ (3) và (4) suy ra $F M=E M(* *)$.
Từ $(*)$ và $(* *)$ ta có $M N$ là đường trung trực của $E F$.
Gọi $G$ là giao điểm của $M N$ và $E F$.
Tam giác $F M E$ có $M G$ là đường cao đồng thời là đường trung tuyến.
Suy ra $F M E$ cân tại $M$ có $M G$ là đường phân giác $\widehat{F M G}=\dfrac{1}{2} \widehat{F M E}$ Xét đường tròn ngoại tiếp tứ giác $A E H F$ có $\widehat{F A E}=\dfrac{1}{2} \widehat{F M E}$ (góc nội tiếp bằng một nửa góc ở tâm chắn cung $E F)(6)$.
Từ (5) và (6) suy ra $\widehat{F A E}=\widehat{F M G}$ hay $\widehat{F A C}=\widehat{F M N}$.
Lại có $F M=M H=\dfrac{1}{2} A H$ nên tam giác $F M H$ cân tại $M \Rightarrow \widehat{M H F}=\widehat{M F H}=\widehat{D H C}$.
Mặt khác $F N=N C=\dfrac{1}{2} B C$ nên tam giác $F N C$ cân tại $N \Rightarrow \widehat{N F C}=\widehat{N C F}$.
Mà $\widehat{N C F}+\widehat{H D C}=90^{\circ} \Rightarrow \widehat{N F C}+\widehat{M F H}=\widehat{M F N}=90^{\circ}$.
Xét tam giác $\triangle F M N$ và $\triangle F A C$ có $\widehat{F M N}=\widehat{F A C}, \widehat{M F N}=\widehat{A F C}=90^{\circ}$.
Suy ra $\triangle F M N \backsim \triangle F A C \Rightarrow \dfrac{F M}{F A}=\dfrac{F N}{F C} \Rightarrow F M . F C=F N . F A($ đpcm).
c) Chứng minh rằng đường tròn đường kính $P Q$ đi qua giao điểm của $F E$ và $M N$.
Vì $M N \perp E F$ tại $G$ nên $\widehat{M G F}=90^{\circ}$.
Ta có $M P \perp P Q$ tại $P$ nên $\widehat{M P F}=90^{\circ}$.
Tứ giác $M P F G$ có $\widehat{M G F}+\widehat{M P F}=180^{\circ}$, mà 2 góc này đối nhau $\Rightarrow M P F G$ là tứ giác nội tiếp. Suy ra $\widehat{M G P}=\widehat{M F P}(2$ góc nội tiếp cùng chắn cung $M P)$.
Vì $M N \perp E F$ tại $G$ nên $\widehat{N G F}=90^{\circ}$.
Ta có $N Q \perp P Q$ tại $Q$ nên $\widehat{N Q F}=90^{\circ}$.
Tứ giác $N Q F G$ có $\widehat{N G F}+\widehat{N Q F}=180^{\circ}$, mà 2 góc này đối nhau $\Rightarrow N Q F G$ là tứ giác nội tiếp. Suy ra $\widehat{N G Q}=\widehat{N F Q}$ (2 góc nội tiếp cùng chắn cung $N Q)$.
$\Rightarrow \widehat{M G P}+\widehat{N G Q}=\widehat{M F P}+\widehat{N F Q}$
Mà $\widehat{M F N}=90^{\circ}$ nên $\widehat{M F P}+\widehat{N F Q}=90^{\circ} \Rightarrow \widehat{M G P}+\widehat{N G Q}=90^{\circ} \Rightarrow \widehat{P G Q}=90^{\circ} \Rightarrow G$ thuộc đường tròn đường kính $P Q$.
Vậy đường tròn đường kính $P Q$ đi qua giao điểm của $F E$ và $M N$.
