Bất phương trình nào sau đây là bất phương trình bậc nhất một ẩn?

Cho đường tròn $(O)$, đường kính $10$ cm, dây $AB=6$ cm. Khoảng cách từ tâm $O$ đến dây $AB$ bằng

Rút gọn biểu thức $A=1:\Big(\dfrac{\sqrt{7}-\sqrt{21}}{1-\sqrt{3}}-\sqrt{11+4\sqrt{7}} \Big)$ kết quả để dưới dạng phân số tối giản $\dfrac{a}{b}$ có mẫu số dương (với $a,\,b$ là các số nguyên) khi đó tổng $a+b$ bằng

Hệ phương trình $\left\{ \begin{aligned} & 2x+ay=0 \\ & bx-y=-1 \end{aligned} \right.$ có nghiệm $(x;y)=(-1;2)$ thì biểu thức $a^2+b^2$ bằng

Phương trình $\dfrac{7}{x+2}=\dfrac{3}{x-5}$ có nghiệm là được biểu diễn dưới dạng phân số $\dfrac{a}{b}$ tối giản có mẫu số dương (với $a,\,b$ là các số nguyên). Giá trị biểu thức $A=a+b$ là

Cho $\Delta ABC$ vuông tại $A$ có 3 đỉnh thuộc $(O)$, đường cao $AH$, biết $AB=6$ cm; $AC=8$ cm. Khi đó độ dài đường tròn có đường kính $AH$ bằng

Căn bậc hai số học của $100$ bằng

Tất cả các giá trị của $x$ để $\sqrt{\dfrac{1}{x}}$ có nghĩa là

Biết rằng $(x_0;y_0)$ là nghiệm của hệ phương trình $\left\{ \begin{aligned} & x+2y=3 \\ & 2x-y=1 \end{aligned} \right.$. Tổng $A=x_0+y_0$ bằng

Số nghiệm của phương trình $\dfrac{2}{x-1}=\dfrac{2x}{x-1}$ là

Tổng các nghiệm của phương trình $(2x+1)(x-2)=0$ là

Một kho chứa $100$ tấn xi măng, mỗi ngày đều xuất đi $20$ tấn xi măng. Gọi $x$ là số ngày xuất xi măng của kho đó. Biết rằng sau $x$ ngày xuất hàng, khối lượng xi măng còn lại trong kho ít nhất là $10$ tấn. Bất phương trình biểu diễn số xi măng còn lại trong kho sau $x$ ngày là

Đồ thị của hàm số $y=(2m-1)x^2$ đi qua điểm $A(-2;4)$. Khi đó giá trị của $m$ là

Đồ thị hàm số $y=-\dfrac{1}{\sqrt{3}}x^2$ đi qua điểm nào dưới đây?

Một cái thang dài $6$ m, đặt dựa vào tường để được đạt được thang an toàn, góc giữa thang và mặt đất là $60^\circ$. Khi đó khoảng cách giữa chân thang đến tường bằng

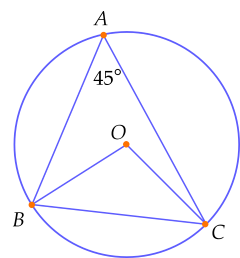
Cho $\Delta ABC$ có $\widehat{BAC}=45^\circ$ và có $3$ đỉnh thuộc đường tròn tâm $O$. Số đo $\widehat{BOC}$ bằng

Cho biết $x=2$ là một nghiệm của phương trình $x^2+ bx+c=0$. Khi đó $2b+c$ bằng

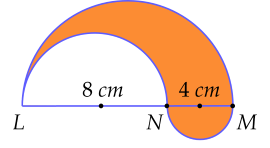
Diện tích phần tô màu ở hình sau, giới hạn bởi nửa đường tròn đường kính $LM$ và hai nửa đường tròn có đường kính tương ứng là $LN=8$ cm và $NM=4$ cm là

Hai con thuyền $P$ và $Q$ cách nhau $300$ m và thẳng hàng với chân $B$ của tháp hải đăng ở trên bờ biển. Từ $P$ và $Q$ người ta nhìn thấy tháp hải đăng dưới các góc $\widehat{BPQ}=14^\circ;\widehat{BQA}=42^\circ$. Đặt $h=AB$ là chiều cao của tháp hải đăng.

Khi đó chiều cao của tháp hải đăng (làm tròn đến hàng đơn vị) là

Tháng 11 vừa qua, trong ngày Black Friday, phần lớn các trung tâm thương mại đều giảm giá nhiều mặt hàng. Mẹ bạn Minh có dẫn Minh đến một trung tâm thương mại để mua một đôi giày. Biết đôi giày đang khuyến mãi giảm giá $45\%$, mẹ Minh có thẻ khách hàng thân thiết của trung tâm thương mại nên được giảm thêm $5\%$ trên giá đã giảm nữa. Do đó, mẹ Minh chỉ phải trả $418\,000$ đồng cho đôi giày. Hỏi giá ban đầu của đôi giày nếu không được khuyến mãi là bao nhiêu?

Rút gọn biểu thức $A=\Big(\dfrac{\sqrt{a}}{\sqrt{a}-1}+\dfrac{1}{\sqrt{a}-a}\Big):\Big(\dfrac{1}{\sqrt{a}+1}+\dfrac{2}{a-1}\Big)$ với $a>0;a\ne 1$.

Giải hệ phương trình $\left\{ \begin{aligned} & 3x-y=1 \\ & x+2y=5 \end{aligned} \right.$.

Giải bất phương trình sau: $2x+3(x+1)>5x-(2x-4)$.

Giải phương trình $2x^2-5x+3=0$.

Thời gian $t$ (tính bằng giây) từ khi một người bắt đầu nhảy bungee trên cao cách mặt nước $d$ (tính bằng $m$) đến khi chạm mặt nước được cho bởi công thức: $d=\dfrac{9,8}{3}.t^2$. Tìm độ cao của người nhảy bungee so với mặt nước biết rằng thời gian từ khi người đó nhảy đến khi chạm mặt nước là $9$ giây.

Giải bài toán bằng cách lập phương trình hoặc hệ phương trình.

Trong đợt thi đấu giải bóng bàn dành cho lứa tuổi học sinh THCS của năm học 2024 – 2025. Một đội tuyển học sinh của một cụm trường THCS tham gia cuộc thi đấu bóng bàn gồm cả Nam và Nữ. Trong lớp có $\dfrac{1}{2}$ số học sinh nam và $\dfrac{5}{8}$ số học sinh nữ thi đấu tạo thành cặp (một nam kết hợp với một nữ). Số học sinh còn lại không thi đấu là $16$ học sinh làm cổ động viên. Đội tuyển đó có tất cả bao nhiêu học sinh?

Cho $(O)$ có đường kính $AB$. Kẻ đường kính $CD$ vuông góc với $AB$. Lấy $M$ thuộc cung nhỏ $\overset\frown{BC}$, $AM$ cắt $CD$ tại $E$. Qua $D$ kẻ tiếp tuyến với $(O)$ cắt đường thẳng $BM$ tại $N$. Gọi $P$ là hình chiếu vuông góc của $B$ lên $DN$.

a) Chứng minh rằng: Các điểm $M,\,N,\,D,\,E$ cùng thuộc một đường tròn.

b) Chứng minh rằng: $EN$ // $CB.$

c) Chứng minh rằng: $AM.BN=2R^2$ và tìm vị trí điểm $M$ trên cung nhỏ $\overset\frown{BC}$ để diện tích tam giác $BNC$ đạt giá trị lớn nhất.

Người ta muốn làm một vườn rau có dạng hình chữ nhật $ABCD$ có diện tích $640$ m², để tạo thêm cảnh quan xung quanh đẹp hơn, người ta mở rộng thêm bốn phần diện tích để trồng hoa, tạo thành một đường tròn đi như hình vẽ, biết tâm hình tròn trùng với giao điểm hai đường chéo của hình chữ nhật. Khi đó chọn kích thước cạnh $ABCD$ như thế nào để diện tích của bốn phần đất trồng hoa nhỏ nhất?